Lineárne programovanie, pre čo ide, modely, obmedzenia, aplikácie

Ten lineárne programovanie Je to matematická metóda, ktorá slúži na optimalizáciu (maximalizácia alebo minimalizácia podľa potreby) funkciu, ktorej premenné podliehajú obmedzeniam, pokiaľ funkcia a obmedzenia sú lineárne závislé od premenných.

Vo všeobecnosti funkcia na optimalizáciu praktickej situácie, ako napríklad zisk výrobcu, ktorého vstupy, práca alebo stroje sú obmedzené.

postava 1. Lineárne programovanie sa široko používa na optimalizáciu ziskov. Zdroj: piqsels.

Jedným z najjednoduchších prípadov je funkcia lineárnej funkcie na maximalizáciu, ktorá závisí iba od dvoch premenných, nazývaných Rozhodovacie premenné. Môže to byť forma:

Z = k₁x + k₂a

S K₁ a k₂ konštanty. Táto funkcia je známa ako Objektívna funkcia. Samozrejme existujú situácie, ktoré si zaslúžia viac ako dve premenné pre ich štúdium, sú zložitejšie:

Z = k₁X₁ + klimatizovať₂X₂ + klimatizovať₃X₃ +.. .

A obmedzenia sú tiež matematicky modelované prostredníctvom systému rovníc alebo nerovností, rovnako lineárne v X a a.

Sada riešení tohto systému sa nazýva uskutočniteľné riešenia ani uskutočniteľné body. A medzi uskutočniteľnými bodmi je aspoň jeden, ktorý optimalizuje objektívnu funkciu.

Lineárne programovanie bolo vyvinuté nezávisle americkým fyzikom a matematikom.

Metóda riešenia problémov známa ako Simplexná metóda Je to vytvorenie Dantziga, ktorý pracoval pre letectvo USA, University of Berkeley a Stanford University.

Obrázok 2. Matematici George Dantzig (vľavo) a Leonid Kantorovich (vpravo). Zdroj: f. Zapata.

[TOC]

Modely lineárneho programovania

Potrebné prvky na vytvorenie lineárneho modelu programovania, ktoré je vhodné pre praktickú situáciu, sú:

-Objektívna funkcia

-Rozhodovacie premenné

-Obmedzenia

V objektívnej funkcii je definované to, čo chcete dosiahnuť. Predpokladajme napríklad, že je potrebné maximalizovať zisky získané z výroby určitých výrobkov. Potom sa vytvorí funkcia „zisku“ podľa ceny, za ktorú sa výrobky predávajú.

Z matematického hľadiska je možné túto funkciu vyjadriť skrátene pomocou súčtu:

Z = ∑k_Jo X_Jo

V tejto rovnici K_Jo Sú to koeficienty a x_Jo sú rozhodovacie premenné.

Rozhodovacie premenné sú prvky systému, ktorého kontrola je a ich hodnoty sú kladné reálne čísla. V navrhovanom príklade sú rozhodovacie premenné množstvo každého produktu, ktorý sa má vyrábať, aby sa získal maximálny zisk.

Nakoniec máme obmedzenia, ktoré sú lineárnymi rovnicami alebo nerovnosťami, pokiaľ ide o rozhodovacie premenné. Opisujú obmedzenia problému, ktoré sú známe a môžu to byť napríklad množstvo surovín dostupných vo výrobe.

Môže vám slúžiť: funkcie vyšších ako dva (príklady)

Typy obmedzení

Môžete mať množstvo m obmedzení, počnúc od J = 1 až do J = m. Matematicky sú obmedzenia troch typov:

1. Do_J = ∑ a_ij . X_Jo
2. B_J ≥ ∑ B_ij . X_Jo
3. C_J ≤ ∑ C_ij . X_Jo

Prvé obmedzenie je typu lineárnej rovnice a znamená, že hodnota pre_J, čo je známe, musí sa rešpektovať.

Zostávajúce dve obmedzenia sú lineárne nerovnosti a znamená, že B hodnoty_J a c_J, Známe, možno rešpektovať alebo prekonať, ak je symbol, ktorý sa objaví, ≥ (väčší alebo rovný) alebo rešpekt alebo neprekonáva, ak je symbol ≤ (menej alebo rovný).

Príklad modelu

Oblasti aplikácie sú veľmi rozmanité, pokrývajúce od podnikovej správy po výživu, ale aby sme pochopili metódu, potom sa navrhuje jednoduchý model praktickej situácie s dvoma premennými.

Miestne pečivo je známe dvoma špecialitami: koláč z čiernej džungle a koláč Scastista.

Vo svojom vypracovaní vyžadujú vajcia a cukor. Pre čiernu džungľu je potrebných 9 vajíčok a 500 g cukru, zatiaľ čo pre krídla je potrebných 8 vajec a 800 g cukru. Príslušné predajné ceny sú 8 a 10 dolárov.

Problém je: Koľko koláčov každého typu by mal urobiť pečivo, aby maximalizoval jeho zisk, s vedomím, že má 10 kilogramov cukru a 144 vajec?

Rozhodovacie premenné

Rozhodovacie premenné sú „x“ a „y“, ktoré majú skutočné hodnoty:

-X: Množstvo koláčov z čiernej džungle

-Y: koláče z obehového typu.

Obmedzenia

Obmedzenia sú uvedené skutočnosťou, že počet koláčov je kladnou sumou a na ich prípravu existuje obmedzené množstvo suroviny.

Preto matematickým spôsobom tieto obmedzenia získavajú formulár:

1. x ≥ 0
2. a ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 a ≤ 10

Obmedzenia 1 a 2 tvoria Stav negativity predtým exponované a všetky zvýšené nerovnosti sú lineárne. V obmedzeniach 3 a 4 sú hodnoty, ktoré by sa nemali prekonať: 144 vajec a 10 kg cukru.

Objektívna funkcia

Nakoniec cieľovou funkciou je zisk získaný výrobou „x“ množstva koláčov čiernej džungle plus „y“ množstvo sakrínskych. Je postavený násobením ceny podľa množstva vyrobených koláčov a pridávanie pre každý typ. Je to lineárna funkcia, ktorú zavoláme G (x, y):

G = 8x + 10y

Metódy riešenia

Medzi rôzne metodiky riešenia patria grafické metódy, algoritmus simplexu a metóda vnútorného bodu, aby ste spomenuli niektoré.

- Grafická alebo geometrická metóda

Ak máte problém s dvoma premennými, ako je predchádzajúca časť, obmedzenia určujú polygonálnu oblasť v rovine Xy, zavolať uskutočniteľný región ani Životnosť.

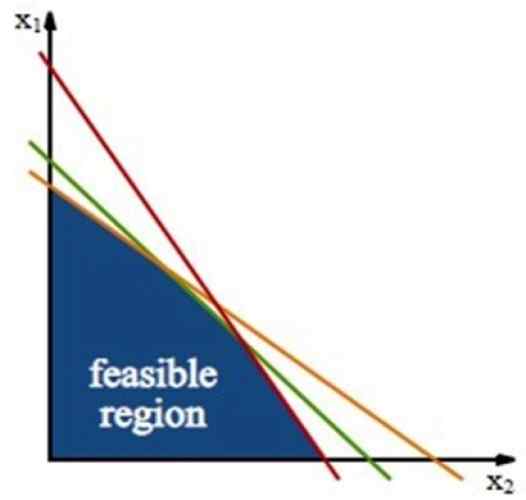Obrázok 3. Uskutočniteľná oblasť, kde sa nachádza riešenie problému optimalizácie. Zdroj: Wikimedia Commons.

Táto oblasť je vybudovaná Obmedzenie, ktoré sú riadky získané z nerovností obmedzení, pracujú iba so znakom rovnosti.

Môže vám slúžiť: konečná súprava: Vlastnosti, príklady, vyriešené cvičenia

V prípade pekárne, ktorá chce optimalizovať zisky, sú linky obmedzení:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Všetky body v regióne zamknuté týmito riadkami sú možnými riešeniami, takže ich existujú nekonečné. S výnimkou prípadu, keď je uskutočniteľný región prázdny.

Našťastie pre problém pečiva je uskutočniteľný región prázdny, máme ho nižšie.

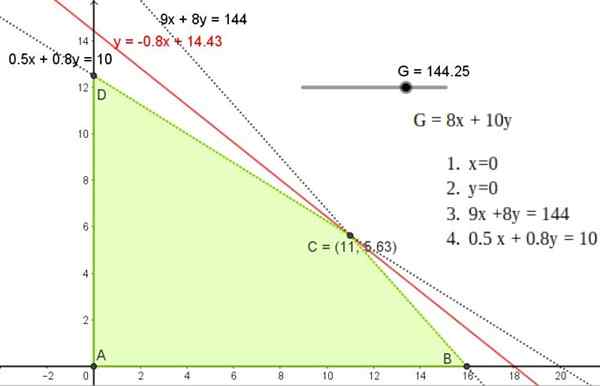
Obrázok 4. Uskutočniteľná oblasť problému pečiva. Priamka 0 prechádza cez pôvod. Zdroj: f. Zapata s geogebou.

Optimálne riešenie, ak existuje, je s pomocou objektívnej funkcie. Napríklad, pokiaľ ide o nájdenie maximálneho zisku G, máte nasledujúci riadok, ktorý sa volá ISO-BENEFICE Rovná:

G = k₁x + k₂a → y = -K₁x / k₂ + G/ k₂

S týmto riadkom sa získajú všetky páry (x, y), ktoré poskytujú daný zisk g, takže existuje rodina riadkov podľa hodnoty g, ale všetko s rovnakým sklonom -K₁ / k₂, takže sú paralelné rovno.

Optimálne riešenie

Teraz je možné preukázať, že optimálne riešenie lineárneho problému je vždy extrémne alebo vrcholom uskutočniteľnej oblasti. Tak:

Roztok čiary je najvzdialenejší z pôvodu a ktorý má aspoň jeden bod spoločného s uskutočniteľnou oblasťou.

Ak má čiara najbližšie k pôvodu celý segment spoločný s uskutočniteľným regiónom, hovorí sa, že existujú nekonečné riešenia. Tento prípad sa vyskytuje, ak sa sklon linky izo-benefits rovná slastvu ktoréhokoľvek z ostatných riadkov, ktoré obmedzujú oblasť.

Pre naše pečivo sú kandidátske vrcholy A, B a C.

- Dantzig

Grafická alebo geometrická metóda je použiteľná pre dve premenné. Je však komplikovanejšie, keď existujú tri premenné a nemožné použiť pre väčší počet premenných.

Pokiaľ ide o problémy s viac ako dvoma premennými, Simplexná metóda, ktorý pozostáva zo série algoritmov na optimalizáciu objektívnych funkcií. Na vykonávanie výpočtov sa zvyčajne používajú jednoduché matice a aritmetika.

Metóda simplexu začína výberom uskutočniteľného riešenia a kontrolou, či je optimálna. Ak je to problém, problém sme už vyriešili, ale ak nie, pokračuje smerom k riešeniu bližšie k optimalizácii. Ak riešenie existuje, algoritmus s ním pri niekoľkých pokusoch.

Môže vám slúžiť: Aký je sortiment štatistík? (S príkladmi)

Žiadosti

Lineárne a nelineárne programovanie aplikované v mnohých oblastiach na to, aby sa robili najlepšie rozhodnutia pri znižovaní nákladov a zvyšujúcich sa ziskov, ktoré nie sú vždy peňažné, pretože sa dajú merať v čase, napríklad ak sa snažíte minimalizovať potrebný čas na vykonanie séria operácií.

Tu sú niektoré polia:

-V marketingu sa používa na nájdenie najlepšej kombinácie médií (sociálnych sietí, televízie, tlače a ďalších) na inzerciu určitého produktu.

-Na pridelenie práce vhodnej pre personál spoločnosti alebo továrne alebo plánov pre nich.

-Pri výbere najživnejších potravín a najnižších nákladov v hospodárskych a hydinových odvetviach.

Vyriešené cvičenia

- Cvičenie 1

Graf Lineárne programovací model zvýšený v predchádzajúcich častiach.

Riešenie

Je potrebné grafovať množinu hodnôt určených systémom obmedzení uvedených v probléme:

1. x ≥ 0
2. a ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 a ≤ 10

Región daný nerovnosťami 1 a 2 zodpovedá prvému kvadrantu karteziánskej roviny. Pokiaľ ide o nerovnosti 3 a 4, začína to nájdením obmedzovacích línií:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

Uskutočniteľná oblasť je štvoruholník, ktorého vrcholy sú body A, B, C a D.

Minimálny zisk je 0, preto riadok 8x + 10 a 10 je dolná hranica a riadky ISO -BENEFIT majú čakajúce -8/10 = -0.8.

Táto hodnota sa líši od svahov ostatných reštrikčných čiar a keď je realizovateľný región obmedzený, existuje jedinečné riešenie.

Obrázok 5. Grafický roztok cvičenia 1, ktorý ukazuje uskutočniteľnú oblasť a bodové roztok C v jednom z vrcholov uvedenej oblasti. Zdroj: f. Zapata.

Toto riešenie zodpovedá svahovej línii -0.8, ktorý prechádza jedným z bodov A, B alebo C, ktorého súradnice sú:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Optimálne riešenie

Vypočítame hodnotu G pre každý z týchto bodov:

-(11; 5.625): G_Do = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

Najväčším ziskom je výroba 11 koláčov z čiernej džungle a 5.625 Sacripantine Cakes. Toto riešenie súhlasí s riešením, ktoré sa nachádza prostredníctvom softvéru.

- Cvičenie 2

Overte výsledok predchádzajúceho cvičenia pomocou funkcie Solver (Solutioner) dostupnej vo väčšine tabuliek, ako je Excel alebo Calc de Libreoffice, ktorá obsahuje algoritmus simplexu pre lineárnu optimalizáciu programovania.

Riešenie

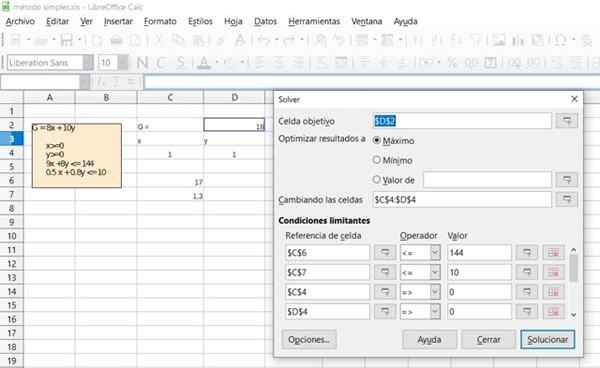Obrázok 6. Podrobnosti o riešení cvičenia 1 prostredníctvom bezplatnej tabuľky Office Calpsheet. Zdroj: f. Zapata. 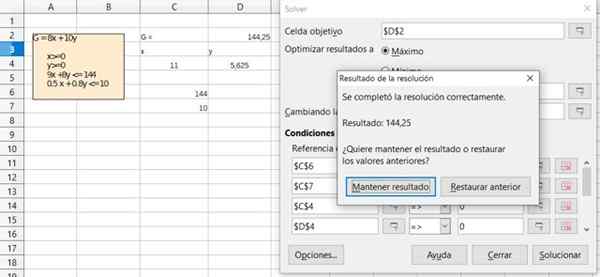Obrázok 7. Podrobnosti o riešení cvičenia 1 prostredníctvom bezplatnej tabuľky Office Calpsheet. Zdroj: f. Zapata.

Odkazy

1. Brilantný. Lineárne programovanie. Zotavené z: brilantného.orgán.
2. Eppen, G. 2000. Operačný výskum v oblasti administratívnej vedy. 5. Vydanie. Sála.
3. Haeussler, e. 1992. Matematika pre správu a ekonomiku. Druhý. Vydanie. Ibero -American Editorial Group.
4. Hiru.Eus. Lineárne programovanie. Získané z: Hiru.Eus.
5. Wikipedia. Lineárne programovanie. Obnovené z: je. Wikipedia.orgán.