Charakteristiky dynamického programovania, príklad, výhody, nevýhody

Ten Dynamické programovanie Je to model algoritmu, ktorý vyrieši zložitý problém tým, že ho rozdelí na podprava a ukladá svoje výsledky, aby sa predišlo tomu, aby sa tieto výsledky vypočítali.

Tento program sa používa, keď sa problémy môžu rozdeliť na podobné podskupiny, aby sa ich výsledky mohli znovu použiť. Pre väčšinu sa tento program používa na optimalizáciu.

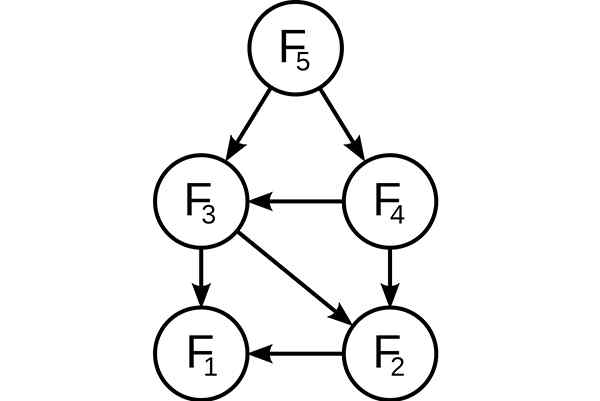
Dynamické programovanie. Podrobnosti prekrývajú. Zdroj: Wikimedia Commons, AT: User: Dcoatzee, sledovaný používateľom: Stannered / Public Domain

Pred vyriešením dostupného podproblému sa dynamický algoritmus pokúsi preskúmať výsledky predtým vyriešených podpätie. Roztoky subproblémov sa kombinujú, aby sa dosiahli najlepšie riešenie.

Namiesto toho, aby ste znova a znova vypočítali rovnaký podproblém. Keď sa objaví opäť počas riešenia iného podpísania, riešenie, ktoré sa už uloží v pamäti.

Je to úžasný nápad na nápravu času s pamäťou, kde pri použití ďalšieho priestoru môžete vylepšiť čas potrebný na nájdenie riešenia.

[TOC]

Charakteristiky dynamického programovania

Nasledujúce základné charakteristiky sú tie, ktoré je možné uplatniť problém na dynamické programovanie:

Optimálna podštruktúra

Táto charakteristika vyjadruje, že problém s optimalizáciou sa dá vyriešiť kombináciou optimálnych riešení sekundárnych problémov, ktoré ho tvoria. Tieto optimálne subštruktúry sú opísané rekurziou.

Napríklad v grafe bude optimálna subštruktúra prezentovaná na najkratšej trase, ktorá prechádza z vrcholu do vrcholu T:

To znamená, na tejto najkratšej trase r si môžete vziať akýkoľvek stredný vrchol i. Ak R je skutočne najkratšia cesta, potom sa dá rozdeliť na subrutas R1 (od S do I) a R2 (od i do t), takže sú zase najkratšie trasy medzi zodpovedajúcimi vrcholmi.

Preto, aby ste našli najkratšie trasy, ktoré môžete ľahko formulovať riešenie rekurzívne, čo je to, čo robí algoritmus Floyd-Warshall.

Prekrývajúce sa

Priestor subproblémov musí byť malý. To znamená, že akýkoľvek rekurzívny algoritmus, ktorý rieši problém.

Napríklad na generovanie série fibonacci sa môže zohľadniť táto rekurzívna formulácia: fn = f (n-1) + f (n-2), pričom sa berie ako základný prípad, že f1 = f2 = 1. Potom budete musieť: F33 = F32 + F31 a F32 = F31 + F30.

Ako je zrejmé, F31 sa rieši v rekurzívnych sub -seasonoch F33 a F32. Aj keď je celkový počet subproblémov skutočne malý, ak sa prijme rekurzívne riešenie, pretože to skončí znova a znova vyrieši rovnaké problémy.

Môže vám slúžiť: 7 komponentov informačného systému

Toto sa berie do úvahy dynamickým programovaním, takže vyrieši každý podprogram iba raz. To sa dá dosiahnuť dvoma spôsobmi:

Najvyšší prístup

Ak je možné riešenie akéhokoľvek problému s formulovať rekurzívne pomocou riešenia ich subproblémov, a ak sa tieto podskupiny prekrývajú, potom sa môžu riešenia subproblémov ľahko zapamätať alebo uložiť do tabuľky v tabuľke v tabuľke.

Zakaždým, keď sa vyhľadá riešenie nového podprokľač. V prípade, že je uložené riešenie, použije sa namiesto toho, aby ho znova vypočítal. V opačnom prípade sa podproflema vyrieši a uloží riešenie v tabuľke.

Vzostupný prístup

Po riešení problému je rekurzívne formulované z hľadiska jeho podpätie, problém sa dá vyskúšať nahor: Najprv sa pokúsia vyriešiť podproblémy a použiť svoje riešenia na dosiahnutie riešení najväčších podskupín.

Zvyčajne sa to robí vo forme tabuľky, ktorá vytvára iteračné riešenia čoraz veľkých podskupín pomocou riešení k malým podvratným problémom. Napríklad, ak sú hodnoty F31 a F30 už známe, hodnota F32 sa dá priamo vypočítať.

Porovnanie s inými technikami

Významnou príslušnosťou k problému, ktorý sa dá vyriešiť dynamickým programovaním, je to, že by sa malo prekrývať subproblémy. To je to, čo rozlišuje dynamické programovanie techniky delenia a dobývania, kde nie je potrebné ukladať najjednoduchšie hodnoty.

Je to podobné rekurzii, pretože výpočtom základných prípadov sa konečná hodnota môže určiť induktívne. Tento vzostupný prístup funguje dobre, keď nová hodnota závisí iba od predtým vypočítaných hodnôt.

Príklad

Minimálne kroky na dosiahnutie 1

Pre akékoľvek pozitívne číslo „e“ môžete vykonať ktorýkoľvek z nasledujúcich troch krokov.

- Odčítať 1 od čísla. (E = E-1).

- Ak je deliteľná 2, je vydelená 2 (ak E%2 == 0, potom E = E/2).

- Ak je deliteľná 3, je vydelená 3 (ak E%3 == 0, potom e = e/3).

Na základe predchádzajúcich krokov musíte nájsť minimálne množstvo týchto krokov, ktoré treba podniknúť, a 1. Napríklad:

- Ak e = 1, výsledok: 0.

- Ak e = 4, výsledok: 2 (4/2 = 2/2 = 1).

- Keď e = 7, výsledok: 3 (7-1 = 6/3 = 2/2 = 1).

Prístup

Vždy by ste mohli premýšľať o výbere kroku, ktorý robí n čo najnižší a pokračuje takto, až kým nedosiahne 1. Je však vidieť, že táto stratégia tu nefunguje.

Môže vám slúžiť: komerčný softvér

Napríklad, ak E = 10, kroky by boli: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 kroky). Optimálny spôsob je však: 10-1 = 9/3 = 3/3 = 1 (3 kroky). Preto sa musia dokázať všetky možné kroky, ktoré je možné urobiť pre každú hodnotu n, výber minimálneho množstva týchto možností.

Všetko sa začína rekurziou: f (e) = 1 + min f (e-1), f (e/2), f (e/3), ak e> 1, berúc ako základný prípad: f (1 ) = 0. Ak máte rovnicu recidívy, môžete začať kódovať rekurziu.

Je však možné poznamenať, že má prekrývajúce sa subproblémy. Okrem toho optimálne riešenie pre daný vstup závisí od optimálneho riešenia jeho podprava.

Rovnako ako pri zapamätaní, kde sú uložené riešenia vyriešených subproblémov, aby ich použili neskôr. Alebo ako v dynamickom programovaní, začína zdola, postupuje do daného e. Ďalej obidva kódy:

Zapamätanie

Dynamické nahor programovanie

Výhody

Jednou z hlavných výhod používania dynamického programovania je to, že urýchľuje spracovanie, pretože sa používajú referencie, ktoré boli predtým vypočítané. Rovnako ako rekurzívna programovacia technika, znižuje riadky programového kódu.

Vorace Algoritmos vs dynamické programovanie

Nenásytné algoritmy sú podobné dynamickému programovaniu v tom zmysle, že obidva sú nástrojmi na optimalizáciu. Algoritmus Voraz však hľadá optimálne riešenie v každom lokálnom kroku. To znamená, že sa snaží chamtivá voľba s nádejou, že nájde globálny optimálny.

Preto nenásytné algoritmy môžu urobiť predpoklad, ktorý v tom čase vyzerá optimálne, ale to sa v budúcnosti stáva drahým a nezaručuje globálny optimálny optimálny.

Na druhej strane, dynamické programovanie nájde optimálne riešenie pre podproblémy a potom sa informuje o výbere kombináciou výsledkov týchto podproblémov, aby ste skutočne našli najoptimálnejšie riešenie.

Nevýhody

- Na ukladanie vypočítaného výsledku každého podskupiny je potrebných veľa pamäte, bez toho, aby bolo možné zabezpečiť, aby sa uložená hodnota použila alebo nie.

- Výstupná hodnota sa mnohokrát ukladá bez toho, aby sa počas vykonávania použila v nasledujúcich podskupinách. To vedie k zbytočnému použitiu pamäte.

- Pri dynamickom programovaní sa funkcie nazývajú rekurzívne. Vďaka tomu zostane pamäť batérie neustále sa zvyšuje.

Rekurtivita vs dynamické programovanie

Ak máte obmedzenú pamäť na vykonanie kódu a rýchlosť spracovania sa netrápia, môže sa použiť rekurzívnosť. Napríklad, ak sa vyvíja mobilná aplikácia, pamäť je veľmi obmedzená na vykonanie aplikácie.

Môže vám slúžiť: Zmiešané zariadenia: Charakteristiky a príklady

Ak je požadovaný program, aby sa vykonal rýchlejšie a neexistujú žiadne obmedzenia pamäte, je vhodnejšie použiť dynamické programovanie.

Žiadosti

Dynamické programovanie je účinná metóda riešenia problémov, ktoré by sa inak mohlo zdať mimoriadne ťažké vyriešiť v primeranom čase.

Algoritmy založené na dynamickom programovacom paradigme sa používajú v mnohých vedeckých oblastiach vrátane mnohých príkladov v umelej inteligencii, od riešenia problémov s plánovaním až po rozpoznávanie hlasu.

Algoritmy dynamického programovania

Dynamické programovanie je dosť efektívne a veľmi dobre slúži pre širokú škálu problémov. Mnoho algoritmov možno považovať za aplikácie nenásytných algoritmov, napríklad:

- Série čísel fibonacci.

- Hanojové veže.

- Všetky najkratšie páry trás od Floyd-Warshall.

- Batoh.

- Programovanie projektu.

- Najkratšia cesta od Dijkstra.

- Kontrola a riadenie letu robotiky.

- Problémy s matematickou optimalizáciou.

- Zdieľaný čas: Program práce na maximalizáciu používania CPU.

Série čísel fibonacci

Fibonacci čísla sú čísla nájdené v nasledujúcej sekvencii: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144 atď.

V matematickej terminológii je FN sukcesia fibonacciových čísel definovaná rekordným vzorcom: f (n) = f (n -1) + f (n -2), kde f (0) = 0 a f (1) = 1 = 1).

Najvyšší prístup

V tomto príklade je vyhľadávacia matica so všetkými počiatočnými hodnotami inicializovaná pomocou -1. Vždy, keď je potrebné riešenie podpísania, bude sa najprv vyhľadať v tejto vyhľadávacej matrici.

Ak existuje vypočítaná hodnota, potom sa táto hodnota vráti. V opačnom prípade bude výsledok vypočítaný na jeho uloženie do vyhľadávacej matice, a tak ho bude môcť znova použiť.

Vzostupný prístup

V tomto prípade sa pre rovnakú sériu fibonacci, F (0), potom f (1), f (2), f (3) atď. Takto budú vybudované riešenia podprava zdola.

Odkazy

1. Vineet Choudhary (2020). Úvod do dynamického programovania. Zasvätenec.Zobraté z: DeveloperInsider.co.
2. Alex Allain (2020). Dynamické programovanie v C++. C programovanie. Prevzaté z: cprogramming.com.
3. Po akadémii (2020). Myšlienka dynamického programovania. Prevzaté z: aftercademy.com.
4. Aniruddha Chaudhari (2019). Dynamické programovanie a rekurzia Odlišný. Stoh. Prevzaté z: csestack.orgán.
5. Šéfkuchár (2020). Pre dynamické programovanie tutoriálu. Zobraté z: Codhef.com.
6. Programiz (2020). Dynamické programovanie. Zobraté z: Programiz.com.