Fyzický

Charakteristiky politického procesu, aplikácie a príklady

Charakteristiky politického procesu, aplikácie a príklady

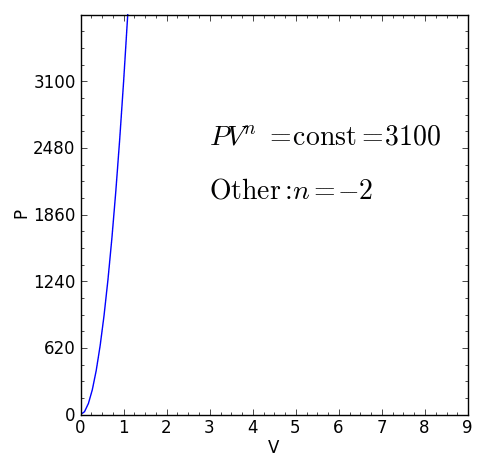
A Politický proces Je to termodynamický proces, ktorý sa vyskytuje, keď vzťah medzi tlakom P a objem Vložka daná P.Vložkan Zostáva konštantný. Exponent n Je to skutočné číslo, zvyčajne medzi nulou a nekonečno, ale v niektorých prípadoch môže byť negatívne.

Hodnota n získať názov Index politiky A je dôležité zdôrazniť, že počas polytropického termodynamického procesu uvedený index musí udržiavať pevnú hodnotu, inak sa tento proces nepovažuje za polytropický.

postava 1. Charakteristická rovnica polytropického termodynamického procesu. Zdroj: f. Zapata.

[TOC]

Charakteristiky polytropických procesov

Niektoré charakteristické prípady polytropických procesov sú: 

- Izotermický proces (pri konštantnej teplote T), v ktorom je exponent n = 1.

- Izobarický proces (konštantný tlak P), v tomto prípade n = 0.

- Izocorický proces (do objemu V konštanta), pre ktorý n =+∞.

- Adiabatické procesy (do konštantnej entropie), v ktorých je exponent n = γ, čo je γ adiabatická konštanta. Táto konštanta je kvocientom medzi tepelnou kapacitou pri konštantnom tlaku CP vydelená tepelnou kapacitou pri konštantnom objeme CV:

γ = CP/CV

- Akýkoľvek iný termodynamický proces, ktorý nie je žiadnym z predchádzajúcich prípadov. Ale dodržiavať P.Vložkan = ctte So skutočným a konštantným polytropickým indexom n Bude to tiež polytropický proces.

Obrázok 2. Rôzne charakteristické prípady polytropických termodynamických procesov. Zdroj: Wikimedia Commons.

Žiadosti

Jednou z hlavných aplikácií polytropickej rovnice je výpočet práce vykonanej uzavretým termodynamickým systémom, keď prechádza z počiatočného stavu na iný konc.

Pracujte v polytropických procesoch pre rôzne hodnoty n

Pre n ≠ 1

Mechanická práca W vykonávaná uzavretým termodynamickým systémom sa vypočíta výrazom:

W = ∫p.DV

Môže vám slúžiť: diamagnetizmus: materiály, aplikácie, príklady

Kde p je tlak a v objem.

Rovnako ako v prípade polytropického procesu, vzťah medzi tlakom a objemom je:

P.Vložka n = konštanta = c

Vymazanie p predchádzajúceho výrazu, ktorý ho nahradí vo vyjadrení práce:

P = c /Vložka n

Máte mechanickú prácu vykonanú počas polytropického procesu, ktorý sa začína v počiatočnom stave 1 a končí v konečnom stave 2. To všetko sa zobrazuje v nasledujúcom výraze:

Ak n ≠ 1, potom máte:

Okrem toho, pretože počiatočné a konečné stavy sú dobre definované, potom je konštanta tiež určená nasledujúcim výrazom:

C = p1 Vložka1n = P2 Vložka2n

Nahradením hodnoty konštanty v vyjadrení práce sa získa:

W = (P2 Vložka2 - P1 Vložka1)/(1-N)

V prípade, že pracovná látka je možné modelovať ako ideálny plyn, má nasledujúca štátna rovnica:

P.V = m.R.Tón

Kde m je počet mólov ideálneho plynu a r je univerzálna konštanta plynov.

Pre ideálny plyn, ktorý sleduje polytropický proces s indexom polytropie odlišným od jednotky a ktorý prechádza zo stavu s počiatočnou teplotou t1 do iného stavu s teplotou t2 Vykonaná práca je daná nasledujúcim vzorcom:

W = m r (t2 - Tón1)/(1-N)

Pre n → ∞

Podľa vzorca pre prácu získanú v predchádzajúcej časti je práca polytropického procesu s n = ∞ nulová, pretože expresia práce je rozdelená medzi nekonečno, a preto výsledok má tendenciu nulu nulovú hodnotu k nule.

Ďalším spôsobom, ako dosiahnuť tento výsledok, je začať od vzťahu P1 Vložka1n = P2 Vložka2n, ktoré je možné prepísať takto:

(P1/P2) = (V2/V1)n

Berúce n-túžšie koreň v každom členovi, ktorého dostanete:

(V2/V1) = (P1/P2)(1/n)

V prípade, že n → ∞, musíte (v2/V1) = 1, čo znamená, že:

Môže vám slúžiť: Ceded Heat: Vzorce, ako ho vypočítať a vyriešiť cvičenia

Vložka2 = V1

To znamená, že objem sa nemení v polytropickom procese s N → ∞. Preto diferenciál objemu DV v integráli mechanickej práce je 0. Tieto typy polytropických procesov sú známe aj ako procesy izokorický, o Procesy pri konštantnom objeme.

Pre n = 1

Opäť máme výraz pre prácu:

W = ∫p dv

V prípade polytropického procesu s n = 1 je vzťah medzi tlakom a objemom:

P v = konštanta = c

Vymazaním p predchádzajúceho výrazu a výmenou máte prácu, aby ste prešli z počiatočného stavu 1 do konečného stavu 2:

W = ∫12p dv = ctte ∫12 v^( - 1) dv = ctte (ln (v2) - ln (v1))

To znamená:

W = c ln (v2/V1).

Pretože počiatočné a konečné stavy sú dobre určené, tak bude aj CTTE. To znamená:

C = p1 Vložka1 = P2 Vložka2

Nakoniec sú k dispozícii nasledujúce užitočné výrazy na nájdenie mechanickej práce polyitropného uzavretého systému, v ktorom n = 1.

W = p1 Vložka1 LN (v2/V1) = P2 Vložka2 LN (v2/V1)

Ak pracovná látka pozostáva z m Móly ideálneho plynu, potom je možné aplikovať ideálnu plynovú rovnicu: p v = m.R.Tón.

V tomto prípade, ako P.Vložka1 = CTTE, polytropický proces s n = 1 je proces pri konštantnej teplote t (izotermal), takže je možné získať nasledujúce výrazy práce:

W = m r t1 LN (v2/V1) = m r t2 LN (v2/V1)

Obrázok 3. Caramban topenie, príklad izotermálneho procesu. Zdroj: Pixabay.

Príklady polytropických procesov

- Príklad 1

Predpokladajme, že valec s pohyblivým piestom plným s kilogramom vzduchu. Spočiatku vzduch zaberá objem V1= 0,2 m3 pri tlaku P1= 400 kPa. Polytropický proces nasleduje n = γ = 1,4, ktorého konečný stav má tlak p2 = 100 kPa. Určite prácu vykonanú vzduchom na piest.

Riešenie

Ak sa index polytropie rovná adiabatickej konštante, existuje proces, v ktorom pracovná látka (vzduch) nevymieňa teplo s prostredím, a preto nemení entropiu.

Môže vám slúžiť: Tretí zákon termodynamiky: vzorce, rovnice, príklady

Pre vzduch, ideálny diatomický plyn, máte:

γ = CP/CV, s CP = (7/2) R a CV = (5/2) R

Tak:

γ = 7/5 = 1,4

Pri použití expresie polytropického procesu je možné určiť konečný objem vzduchu:

Vložka2 = [P2 Vložka11.4)/P2](1/1,4) = 0,54 m3.

Teraz existujú podmienky na použitie pracovného vzorec vykonávané v polytropickom procese pre n ≠ 1 získané vyššie:

W = (P2 Vložka2 - P1 v1)/(1-n)

Výmena príslušných hodnôt je:

W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3)/(1 - 1,4) = 65,4 kJ

- Príklad 2

Predpokladajme rovnaký valec z príkladu 1, s pohyblivým piestom plným s kilogramom vzduchu. Spočiatku vzduch zaberá objem V1 = 0,2 m3 Pri tlaku P1 = 400 kPa. Ale na rozdiel od predchádzajúceho prípadu sa vzduch rozširuje izotermaticky, aby dosiahol konečný tlak P2 = 100 kPa. Určite prácu vykonanú vzduchom na piest.

Riešenie

Ako už bolo vidieť, izotermálne procesy sú polytropické procesy s indexom n = 1, takže je splnené, že:

P1 v1 = p2 v2

Týmto spôsobom je možné konečný objem ľahko oddeliť, aby sa získal:

V2 = 0,8 m3

Potom pomocou expresie práce, ktorá bola predtým získaná pre prípad n = 1, musíte pracovať vzduchom na piestu v tomto procese je:

W = p1 v1 ln (v2/v1) = 400 000 PA × 0,2 m3 ln (0,8/0,2) = 110,9 kJ.  

Odkazy

  1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
  2. Cengel a. 2012. Termodynamika. 7. vydanie. McGraw Hill.
  3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Tekutiny a termodynamika. Editoval Douglas Figueroa (USB).
  4. López, C. Prvý zákon termodynamiky. Získané z: CulturacieCientificA.com.
  5. Rytier, r. 2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
  6. Serway, r., Vulle, C. 2011. Základy fyziky. 9NA ED. Učenie sa.
  7. Univerzita. Tepelné stroje. Získané z: Laplace.my.je.
  8. Wikiwand. Politický proces. Získané z: Wikiwand.com.