Teoretická pravdepodobnosť, ako to dostať von, príklady, cvičenia

Ten Teoretická pravdepodobnosť (alebo Laplace), že sa vyskytuje udalosť, ktorá patrí do vzorového priestoru S, v ktorom majú všetky udalosti rovnakú pravdepodobnosť výskytu, je definovaná v matematickom notácii, ako je: p (e) = n (e) / n ( S)

Kde p (e) je pravdepodobnosť, daná ako pomer medzi celkovým počtom možných výsledkov udalosti E, ktorú nazývame n (e), vydelené celkovým počtom n (s) možných výsledkov v priestore vzorky S.

postava 1. Pri spustení šiestich kocky je teoretická pravdepodobnosť, že tvár s tromi bodkami je na vrchu ⅙. Zdroj: Pixabay.

Teoretická pravdepodobnosť je skutočné číslo medzi 0 a 1, ale často sa vyjadruje vo forme percentuálneho podielu, v takom prípade bude pravdepodobnosť hodnota medzi 0% a 100%.

Výpočet pravdepodobnosti výskytu udalosti je veľmi dôležitý v mnohých oblastiach, ako sú činnosť na akciovom trhu, poisťovacie spoločnosti, hazardné hry a mnoho ďalších.

[TOC]

Ako získať teoretickú pravdepodobnosť?

Ilustratívny prípad je prípad RIFA alebo lotérií. Predpokladajme, že 1.000 lístkov pre RIFAR A smartfón. Keď sa tombola vykonáva náhodne, ktorýkoľvek z lístkov má rovnakú šancu byť víťazom. 

Ak chcete nájsť pravdepodobnosť, že osoba, ktorá si kúpi lístok s číslom 81, bude víťazom, nasledujúci výpočet Teoretická pravdepodobnosť:

P (1) = 1/1.000 = 0,001 = 0,1%

Predchádzajúci výsledok sa interpretuje takto: Ak sa tombola opakuje nekonečne, každé 1.Vstupenka 81 -krát by sa v priemere vybrala v priemere raz, raz.

Ak z nejakého dôvodu niekto získa všetky lístky, že vyhrá cenu. Pravdepodobnosť získania ceny, ak máte všetky vstupenky vypočítané takto:

Môže vám slúžiť: obvod kruhu: Ako ho vytiahnuť a vzorce, vyriešené cvičenia

P (1.000) = 1.000/1.000 = 1 = 100%.

To znamená, čo je pravdepodobnosť 1 alebo 100%.

Ak niekto vlastní 500 lístkov, možnosti výhry alebo straty sú rovnaké. Teoretická pravdepodobnosť výhry ceny v tomto prípade sa vypočíta takto:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Ten, kto nekupuje žiadny lístok, nemá šancu na výhru a jeho teoretická pravdepodobnosť je určená takto:

 P (0) = 0/1.000 = 0 = 0%

Príklady

Príklad 1

Máte menu s drahý na jednej strane a chrániť alebo utesniť v druhom. Po spustení meny, aká je teoretická pravdepodobnosť drahého?

P (drahý) = n (drahý) / N ( tvár ) = ½ = 0,5 = 50%

Výsledok sa interpretuje takto: ak sa uskutočnilo veľké množstvo vydaní, v priemere na každých 2 ihriskách, ktoré by jeden z nich čelil.

V percentuálnom vyjadrení je interpretácia výsledku taká, že vytváranie nekonečne veľkého počtu spustení, v priemere každých 100 z nich by malo za následok drahé.

Príklad 2

V krabici sú 3 modré guľky, 2 červené guľky a 1 zelená. Aká je teoretická pravdepodobnosť, že keď dostanete mramor z krabice, je to červená?

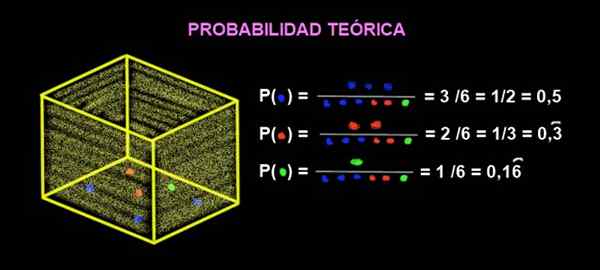Obrázok 2. Pravdepodobnosť extrakcie farebných guličiek. Zdroj: f. Zapata.

Pravdepodobnosť, ktorá prichádza červená, je:

P (červená) = počet priaznivých prípadov / počet možných prípadov

To znamená:

P (červená) = počet červených guličiek / celkový počet guličiek

Nakoniec pravdepodobnosť, že červený mramor je:

P (červené) = 2/6 = ⅓ = 0,3333 = 33,33%

Zatiaľ čo pravdepodobnosť, že extrahovaním zeleného mramoru je:

P (zelená) = ⅙ = 0,1666 = 16,66%

Nakoniec teoretická pravdepodobnosť získania v slepej extrakcii modrý mramor je: 

P (modrá) = 3/6 = ½ = 0,5 = 50%

Môže vám slúžiť: radikálne vlastnosti

To znamená, že z každých 2 pokusov bude výsledok v jednom z nich modrý a iná farba pri inom pokuse pod predpokladom, že extrahovaný mramor je doplňovaný a že počet pokusov je veľmi, veľmi veľký.

Cvičenia

Cvičenie 1

Určite pravdepodobnosť, že pri spustení kocky sa hodnota získa menšia alebo rovná 4.

Riešenie

Na výpočet pravdepodobnosti, že dôjde k tejto udalosti, sa bude uplatňovať definícia teoretickej pravdepodobnosti:

P (≤ 4) = počet priaznivých prípadov / počet možných prípadov

P (≤5) = 5/6 = = 83,33%

Cvičenie 2

Nájdite pravdepodobnosť, že v dvoch po sebe idúcich výškách normálnych šesťdesiatych kocky, 2 -krát 2 -krát 2 -krát.

Riešenie

Na reagovanie na toto cvičenie je vhodné urobiť obrázok, ktorý ukáže všetky možnosti. Prvý obrázok označuje výsledok prvých kocky a druhý výsledok druhého.

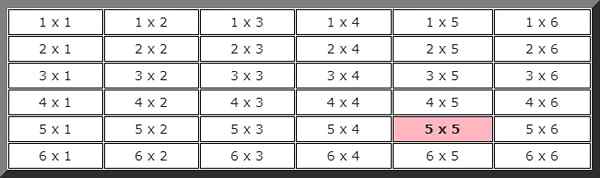
Na výpočet teoretickej pravdepodobnosti potrebujeme poznať celkový počet možných prípadov, v tomto prípade, ako je zrejmé z predchádzajúcej tabuľky, existuje 36 možností.

Pozorovanie maľby Z toho vyplýva, že počet prípadov priaznivých pre udalosť, že v dvoch po sebe nasledujúcich vydaniach prichádza 5, je iba 1, zvýraznená farbou, preto pravdepodobnosť, že sa táto udalosť stane, je:

P (5 x 5) = 1/33.

Tento výsledok by sa mohol dosiahnuť aj pomocou jednej z vlastností teoretickej pravdepodobnosti, ktorá uvádza, že kombinovaná pravdepodobnosť dvoch nezávislých udalostí je produktom ich individuálnych pravdepodobností.

V tomto prípade pravdepodobnosť, že v prvom vydaní 5 je ⅙. Druhé spustenie je úplne nezávislé od prvého, a preto je pravdepodobnosť, že 5 v druhom je tiež ⅙. Takže kombinovaná pravdepodobnosť je:

Môže vám slúžiť: čiastočné deriváty: vlastnosti, výpočet, cvičenia

P (5 × 5) = p (5) p (5) = (1/6) (1/6) = 1/36.

Cvičenie 3

Nájdite pravdepodobnosť, že pri prvom spustení vyjde číslo menej ako 2. 

Riešenie

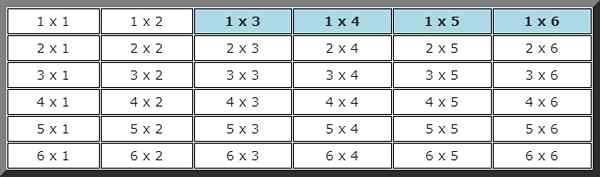
Opäť musíte zostaviť možnú tabuľku udalostí, kde sú tie prvé spustenie menej ako 2 a v druhej vyššej ako 2 sú podčiarknuté.

Celkovo existujú 4 možnosti celkom 36. Inými slovami, pravdepodobnosť tejto udalosti je:

P (2) = 4/36 = 1/9 = 0,1111 = 11,11%

Použitie vety pravdepodobností, ktorá uvádza:

Pravdepodobnosť výskytu dvoch nezávislých udalostí sa rovná produktu individuálnych pravdepodobností.

Získava sa rovnaký výsledok:

P (2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%

Hodnota získaná týmto postupom sa zhoduje s predchádzajúcim výsledkom prostredníctvom teoretickej alebo klasickej definície pravdepodobnosti.

Cvičenie 4

Aká je pravdepodobnosť, že spustením dvoch vzhľadom na súčet hodnôt je 7.

Riešenie

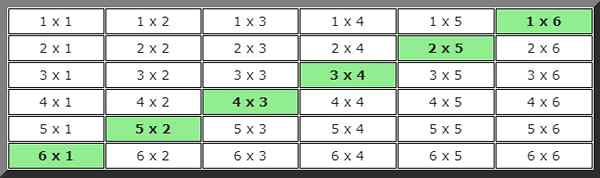
Na nájdenie riešenia v tomto prípade sa vyvinul obraz možností, v ktorých prípady, ktoré spĺňajú stav hodnôt, sú 7.

Pri pohľade na tabuľku je možné spočítať 6 možných prípadov, takže pravdepodobnosť je:

P (R & D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Odkazy

1. Canavos, g. 1988. Pravdepodobnosť a štatistika: Aplikácie a metódy. McGraw Hill.
2. Devore, J. 2012. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. 8. Vydanie. Cengage.
3. Lipschutz, s. 1991. Séria Schaum: Pravdepodobnosť. McGraw Hill.
4. Obregón, i. 1989.Teória pravdepodobnosti. Redakčná limusa.
5. Walpole, r. 2007. Pravdepodobnosť a štatistika pre inžinierstvo a vedu. Pearson.