Koncept pravdepodobnosti frekvencie, ako sa vypočíta a príklady

Ten Pravdepodobnosť frekvencie je Podložie v rámci štúdia pravdepodobnosti a jej javov. Jeho študijná metóda s ohľadom na udalosti a atribúty je založená na veľkom množstve iterácií, a tak každá z nich pozoruje z dlhodobých alebo dokonca nekonečných opakovaní.

Napríklad obálka gummitánu obsahuje 5 gumov každej farby: modrá, červená, zelená a žltá. Chcete určiť pravdepodobnosť, že každá farba musí odísť po náhodnom výbere.

Zdroj: pexels

Je únavné predstaviť si, ako dostanete gumu, zaznamenajte ju, vráťte ju, vyberte gumu a opakujte to isté niekoľko stoviek alebo niekoľkokrát. Môžete dokonca chcieť pozorovať správanie po niekoľkých miliónoch iterácií.

Naopak, je zaujímavé zistiť, že po niekoľkých opakovaní nie je očakávaná pravdepodobnosť 25% úplne splnená, aspoň nie pre všetky farby po 100 iteráciách.

Podľa prístupu pravdepodobnosti frekvencie bude pridelenie hodnôt iba štúdiom mnohých iterácií. Týmto spôsobom sa musí tento proces vykonávať a najlepšie zaregistrovať počítačovým alebo emulovaným spôsobom.

Viaceré prúdy odmietajú pravdepodobnosť frekvencie a tvrdia, že nedostatok empirizmu a spoľahlivosť v náhodných kritériách.

[TOC]

Ako sa vypočíta pravdepodobnosť frekvencie?

Pri programovaní experimentu v akomkoľvek rozhraní schopnom ponúknuť čisto náhodnú iteráciu, môžete začať študovať pravdepodobnosť frekvencie fenoménu prostredníctvom tabuľky hodnôt.

Predchádzajúci príklad je ocenený z frekvenčného prístupu:

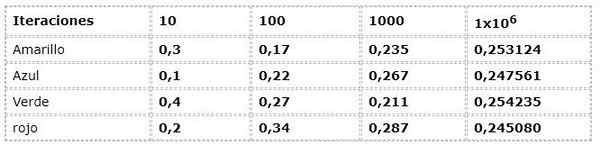
Numerické údaje zodpovedajú výrazu:

N (a) = počet výskytov/ počet iterácií

Kde n (a) predstavuje relatívnu frekvenciu udalosti „A“

„A“ patrí do súboru možných výsledkov alebo vzorkovacieho priestoru Ω

Môže vám slúžiť: násobky 8: Čo je a vysvetlenie

Ω: červená, zelená, modrá, žltá

V prvých iteráciách je značná disperzia, keď sa navzájom pozorujú frekvencie s až 30% rozdielov, čo je veľmi vysoká skutočnosť pre experiment, ktorý má teoreticky udalosti s rovnakou možnosťou (Equrobable).

Ale ako iterácie rastú, hodnoty sa zdajú byť stále viac a hodnoty predstavené teoretickým a logickým prúdom.

Zákon veľkých čísel

Ako neočakávaná dohoda medzi teoretickými a frekvenčnými prístupmi vzniká zákon veľkého počtu. Ak sa zistilo, že po značnom množstve iterácií sa hodnoty frekvenčného experimentu blížia k teoretickým hodnotám.

V príklade si môžete všimnúť, ako sa hodnoty približujú na 0,250, keď rastú iterácie. Tento jav je elementárny pri záveroch mnohých pravdepodobnostných diel.

Zdroj: pexels

Ďalšie pravdepodobné prístupy

Existujú ďalšie 2 teórie alebo prístupy k pojmu pravdepodobnosť okrem Pravdepodobnosť frekvencie.

Logická teória

Váš prístup je zameraný na deduktívnu logiku javov. V predchádzajúcom príklade je pravdepodobnosť získania každej farby 25% uzavretá. Inými slovami.

Subjektívna teória

Vychádza z vedomostí a predchádzajúcich presvedčení, ktoré má každý jednotlivec o javoch a atribútoch. Vyhlásenia ako “Vždy prší vo svätom týždni “ Poslúchajú vzor podobných udalostí, ktoré sa vyskytli predtým.

História

Začiaty dátumu jej implementácie z devätnásteho storočia, keď ho citujem v niekoľkých svojich prácach v Cambridge Anglicko. Ale až do dvadsiateho storočia sa vyvinula a formovala 2 štatistická matematika Pravdepodobnosť frekvencie.

Môže vám slúžiť: polynómové rovnice

Jedným z nich bol Hans Reichenbach, ktorý rozvíja svoju prácu v publikáciách, ako napríklad „Teória pravdepodobnosti“ uverejnená v roku 1949.

Druhým bol Richard Von Mises, ktorý svoju prácu dôkladnejšie rozvinul prostredníctvom viacerých publikácií a navrhol, aby považoval pravdepodobnosť za matematickú vedu. Tento koncept bol v matematike nový a znamenal by začiatok éry rastu v štúdiu Pravdepodobnosť frekvencie.

V skutočnosti táto udalosť robí jediný rozdiel s príspevkami vytvorenými generáciou Venna, Corot a Helm. Kde sa pravdepodobnosť stáva náprotivkom, ako je geometria a mechanika.

< La teoría de las probabilidades trata con masívne javy a opakujúce sa udalosti. Problémy, v ktorých sa buď rovnaká udalosť opakuje znova a znova, alebo sa zapojí veľké množstvo jednotných prvkov súčasne> Richard von Mises

Masívne javy a opakujúce sa udalosti

Tri typy je možné klasifikovať:

• Fyzika: Obdózové vzorce prírody nad náhodným stavom. Napríklad správanie molekúl prvku vo vzorke.
• Šanca: Jeho základným úvahou je náhodnosť, ako opakovaným uvoľňovaním kocky.
• Biologická štatistika: Výber testovacích predmetov podľa ich charakteristík a atribútov.

V teórii jednotlivec, ktorý meria, hrá úlohu v pravdepodobnostných údajoch, pretože práve jeho znalosť a skúsenosti vyjadrujú túto hodnotu alebo predpoveď.

V Pravdepodobnosť frekvencie Udalosti sa budú považovať za zbierky, ktoré sa majú liečiť, kde jednotlivec nehrá v odhade žiadnu úlohu.

Atribúty

V každom prvku sa vyskytuje atribút, ktorý sa bude líšiť podľa tejto povahy tohto. Napríklad v type fyzikálneho javu budú mať molekuly vody rôzne rýchlosti.

Môže vám slúžiť: trojuholníkové kritériá podobnosti

Pri spustení kocky poznáme priestor vzorky Ω, ktorý predstavuje atribúty experimentu.

Ω: 1, 2, 3, 4, 5, 6

Existujú aj ďalšie atribúty, ako napríklad Ω_P  alebo byť nepárny Ω_Jo

Ω_p : 2, 4, 6

Ω_Jo : 1, 3, 5

Ktoré možno definovať ako nekonementárne atribúty.

Príklad

• Chcete vypočítať frekvenciu každého možného súčtu pri spustení dvoch kocky.

Za týmto účelom sa naprogramuje experiment, kde sa do každej iterácie pridajú dve náhodné hodnoty medzi [1, 6].

Dáta sú zaznamenané v tabuľke a študujú sa trendy vo veľkom počte.

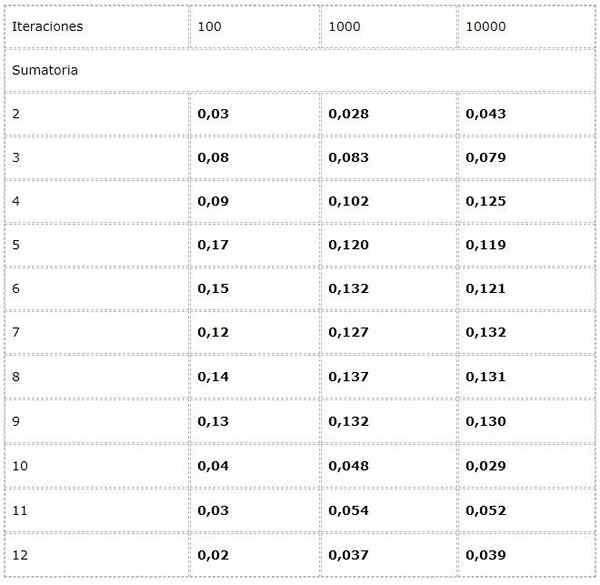
Zistilo sa, že výsledky sa môžu medzi iteráciami výrazne líšiť. Zákon veľkého počtu však je možné vidieť v zjavnej konvergencii uvedenej v posledných dvoch stĺpcoch.

Odkazy

1. Štatistika a hodnotenie dôkazov pre forenzných vedcov. Druhé vydanie. Colin G.G. Aitken. Škola matematiky. University of Edinburgh, UK
2. Matematika pre počítačovú vedu. Eric Lehman. Google Inc.
   F Thomson Leighton Department of Matematics and Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai technológie
3. Aritmetický učiteľ, zväzok 29. Národná rada učiteľov matematiky, 1981. Michiganská univerzita.
4. Teória učenia a výučby: Výskum v poznaní a výučbe / editoval Stephen R. Campbell a Rina Zazkis. ABABLEX Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars domnienky 4ème partie. Rouen: irem.