Lichobežník

Čo je to lichobežník?

A Lichobežník Je to hranol tak, že došlo k polygónom, sú lichobežníky. Definícia hranolu je geometrické telo tvorené dvoma rovnakými a rovnobežnými polygónmi navzájom a zvyšok ich tvárí sú rovnobežníky.

Hranol môže mať rôzne formy, ktoré nezávisia iba od počtu strán mnohouholníka, ale od samotného polygónu.

Ak sú polygóny v hranolu štvorcové, potom sa líši od hranolu, ktorý zahŕňa napríklad kostry, napriek skutočnosti, že oba polygóny majú rovnaký počet strán. Závisí to preto od toho.

Charakteristiky lichobežníka

Ak chcete vidieť charakteristiky lichobežníka hranolu, mali by ste začať tým, že viete, ako sa nakreslí, potom to, aké vlastnosti sa základňa stretáva, aká je oblasť povrchu a nakoniec, ako sa vypočítava jeho objem.

1. Kresliť lichobežník

Aby som ho nakreslil, je potrebné najprv definovať, čo je lichobežník. Trapéza je nepravidelný polygón štyroch strán (štvoruholník), ale takým spôsobom, že má iba dve paralelné strany nazývané bázy a vzdialenosť medzi jeho základňami sa nazýva výška.

Ak chcete nakresliť priamy lichobežník, začnete kresliť lichobežník. Potom sa z každého zveri vyčnieva zvislá čiara dĺžky „H“ a nakoniec sa nakreslí ďalší lichobežník, ktorý sa jeho vrcholy zhodujú s koncami predtým nakreslených čiary.

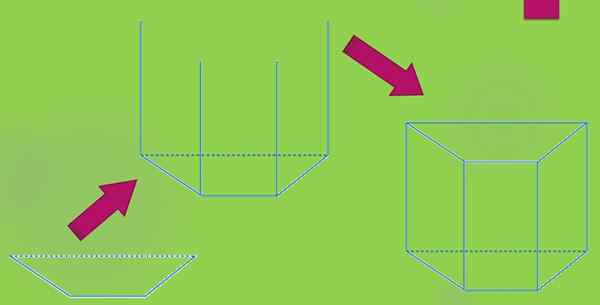
Môžete tiež mať šikmé lichobežné hranoly, ktorého konštrukcia je podobná predchádzajúcej.

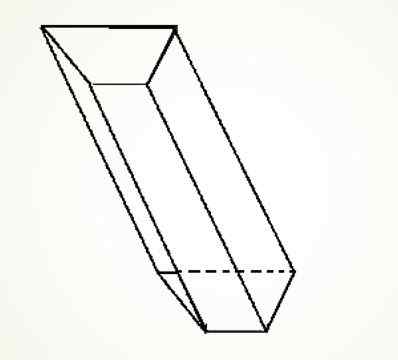
2. Vlastnosti lichobežníka

Ako už bolo uvedené, tvar hranolu závisí od polygónu. V konkrétnom prípade lichobežníka nájdeme tri rôzne typy základov:

Obdĺžnik: Je to taký lichobežník, na ktorom je jedna z jeho strán kolmá na jej paralelné strany alebo ktorá má jednoducho pravý uhol.

Lichobežné izoscely: Je to lichobežník, na ktorom majú jeho nemaľujúce strany rovnakú dĺžku.

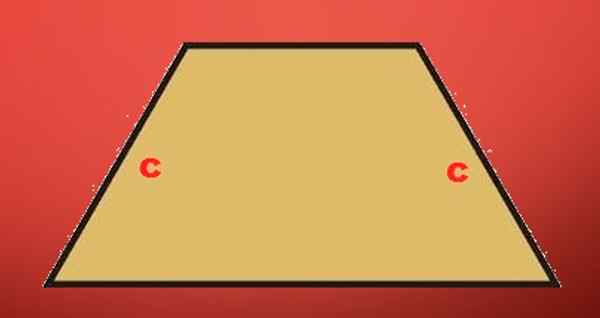
Escaleno Trapezio: Je to ten lichobežník, ktorý nie je izoscely alebo obdĺžnik; Jeho štyri strany majú rôzne dĺžky.

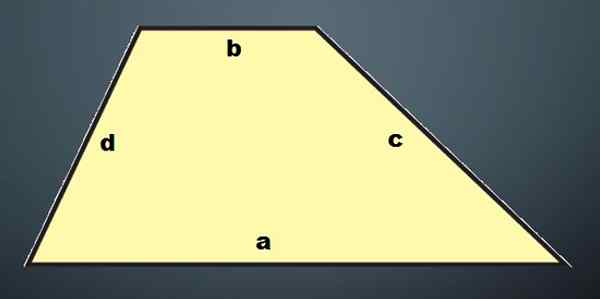
Ako je zrejmé, podľa typu použitého lichobežníka, získa sa iný hranol.

3. Plocha povrchu

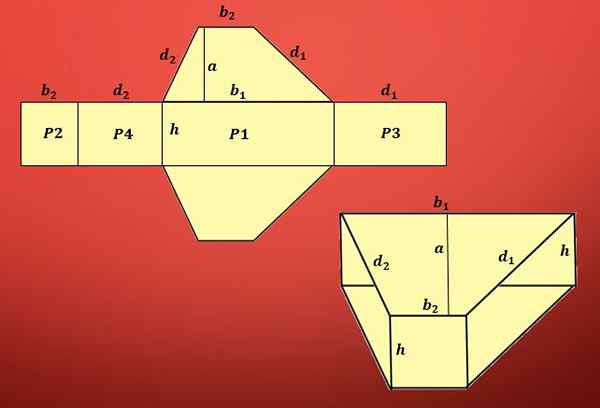
Aby sme vypočítali plochu povrchu lichobežníka, musíme poznať oblasť lichobežníka a plochu každého zapojeného rovnobežníka.

Ako je zrejmé na obrázku, oblasť zahŕňa dva lichobežné a štyri rôzne paralely.

Oblasť lichobežníka je definovaná ako t = (b1+b2) xa/2 a oblasti rovnobežníkov sú p1 = hxb1, p2 = hxb2, p3 = hxd1 a p4 = hxd2, kde „b1“ a „b2“ a „b2“ a „b2“ a „b2“ a „b2“ a „b2“ “Sú základy lichobežníka,„ D1 “a„ D2 “.

Preto plocha povrchu lichobežníka je a = 2T+p1+p2+p3+p4.

4. Zväzok

Pretože objem hranolu je definovaný ako V = (Polygon Area) x (výška), je možné dospieť k záveru, že objem lichobežníka je v = txh.

5. Žiadosti

Jedným z najbežnejších objektov, ktoré majú tvar lichobežníka, je zlatý kozížník alebo rampy používané v pretekoch motocyklov.