Šesťuholník

Vysvetľujeme, čo je šesťuholníkový hranol, jeho charakteristiky, prvky, oblasť, vrcholy, hrany a ako ich vypočítať.

Čo je hexagonálny hranol?

A Šesťuholník Je to trojrozmerné telo zložené z dvoch šesťuholníkových tvarov a strán v tvare obdĺžnika alebo rovnobežníka. Nachádza sa v prírode, napríklad v kryštalickej štruktúre minerálov, ako je napríklad berylia, grafit, zinok a lítium.

Prvky šesťuholníkového hranolu sú základňa, tvár, hrana, výška, vrchol, rádio a apothémia. Z nich môžete vypočítať oblasti a objemy.

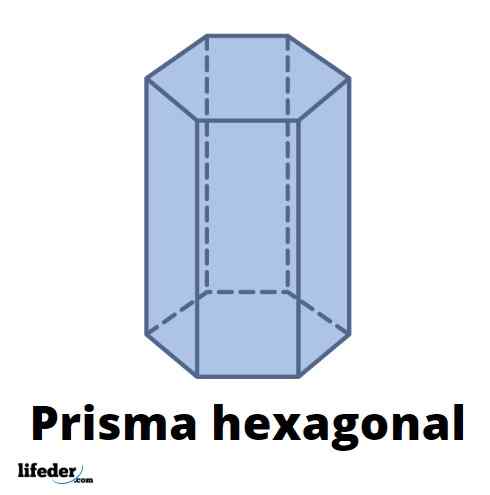
Horná postava ukazuje šesťuholníkový hranol s obdĺžnikovými bočnými tvárami; to znamená, Priamy šesťuholníkový hranol. Šesťhranné základne sú pravidelné, to znamená, že ich vnútorné strany a uhly sú rovnaké. Hexagonálne tváre hranolov však môžu byť nepravidelné šesťuholníky.

Charakteristiky šesťuholníkového hranolu

1- Hexagonálny hranol je trojrozmerná postava so šesťuholníkovými základňami.

2- Existuje široká škála objektov, ktoré reagujú na túto definíciu, a napriek tomu sú celkom odlišné.

Na nasledujúcom čísle je množstvo šesťuholníkových hranolov: vľavo priamy hexagonálny hranol pravidelných tvárí, na pravej a dole dve šesťuholnné hranoly nepravidelných tvárí. Šesťuholník na základni hranolu nižšie má zvláštnosť: je to konkávny, Čo znamená, že niektoré z jeho vnútorných uhlov sú väčšie ako 180 °.

Rozmanitosť šesťuholníkových hranolov. Zdroj: Wikimedia Commons.

Na druhej strane, šesťuholníky vyššie uvedených hranolov sú polygóny vypuklý: Všetky vnútorné uhly merajú menej ako 180 °.

Šesťuholník

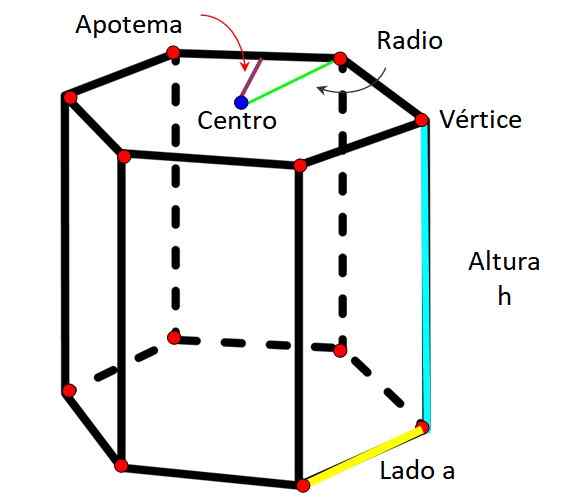Šesťuholník. Zdroj: f. Zapata

Rovnako ako každý hranol, hexagonálny hranol sa vyznačuje tým, že má tieto prvky:

Môže vám slúžiť: Multiplikatívna inverzia: Vysvetlenie, príklady, vyriešené cvičenia

-Základne: V počte dvoch (2), vo forme šesťuholníka a zhody, to znamená rovnaká miera. Hexagonálne tváre môžu byť pravidelné alebo nepravidelné.

-Tváre: Šesťuholníkový hranol má celkom osem (8) tvárí, ktoré sa dajú spočítať pomocou obrázku 1. Z 8 tvárí sú dve (2) základne a šesť (6) je laterálne.

-Hrana: Je to segment, ktorý spája dve základne alebo dve strany hranolu.

-Výška: Je to vzdialenosť medzi dvoma tvárami hranolu. Zhoduje sa s dĺžkou okraja v prípade priameho hranolu.

-Vrchol: Bežný bod medzi základňou a dvoma bočnými stranami.

Ak sú základy hranolu pravidelné, symetria obrázku umožňuje definovať ďalšie prvky bežnej šesťuholníkovej strany do.

-Rozhlas: Je to vzdialenosť meraná od stredu šesťuholníka a akéhokoľvek vrcholu.

-Apotém: Je to segment, ktorý prechádza zo stredu hexagonálnej tváre do stredu jednej strany.

S pomocou týchto prvkov, oblastí a objemov sa vypočítajú, ako uvidíme neskôr.

Vzorce

Existuje veľa receptúr súvisiacich s hexagonálnym hranolom. Slúžia na výpočet oblasti svojich bočných základov a tvárí, jej objemu a ďalších dôležitých charakteristík. Oblasti pravidelného šesťuholníka, nepravidelného šesťuholníka a rovnobežníka, ako aj obvody, sú užitočné.

Obvod plochej postavy

Je to miera jeho obrysu, ktorá je v prípade polygónu, ako je šesťuholník. Ak je šesťuholník pravidelný nabok do, Existuje vzorec pre obvod P:

P = 6.do

Pravidelná šesťuholníková oblasť

Zavolajme ALS a L_Do Na dĺžku apothému. Táto oblasť je daná:

Môže vám slúžiť: NEPRAVENÉ ÚDAJE: Príklady a vyriešené cvičenie

A = p. L_Do/2 = 6a. L_Do/2

Kde P je obvod obrázku.

V závislosti od veľkosti strany do, Túto oblasť je možné vypočítať aj podľa:

A = 2.5981.do²

Nepravidelná plocha

Neexistuje žiadny špecifický vzorec, pretože závisí od usporiadania strán, ale šesťuholník sa dá rozdeliť na trojuholníky, vypočítať oblasť každého z nich a pridať ich.

Ďalšou metódou na nájdenie oblasti je u determinantov Gauss, pre ktorú je potrebné poznať súradnice vrcholov šesťuholníkov.

Rovnobežník

A = výška základne x

Jo do je základňa a h Je to výška, oblasť je:

A = a.h

Šesťuholníkový hranol

Je to súčet oblastí základní -dva šesťuholníky -a tieliny -6 obdĺžniky alebo rovnobežky-.

Pravidelná šesťuholníková oblasť hranolu

Ak má šesťuholníkový hranol základy vo forme pravidelných šesťuholníkov a bočné okraje sú kolmé na tieto základy, jeho oblasť je daná súčtom:

A = 2 x 2.5981.do² + 6.h

Kde do Je to strana šesťuholníka a h Je to výška hranolu.

Nepravidelná a rovná šesťuholníková oblasť hranolu

Ak sú základy nepravidelné šesťuholníky, oblasť sa vypočíta podľa:

A = 2a_základňa  + P.h

Kde:

-Do_základňa Je to nepravidelná šesťuholníková základňa.

-P je obvod základu.

-H je výška hranolu

Vrcholy

Každá šesťuholníková tvár má 6 rohov alebo vrcholov, čo dáva celkom 12 vrcholov pre hexagonálny hranol.

Hrany

Existuje vzorec na nájdenie počtu hrán hranolu. Objavil ho veľký matematik Leonhard Euler (1707-1783) a nazýva sa to Eulerova veta pre polyhedros. Hovorí áno:

Môže vám slúžiť: algebraické zdôvodnenie

Ak C je počet tvárí a množstvo Vértices V a celkové hrany. Je pravda, že:

C+V = A+2

Sumy pre šesťuholníkovú hranol sú: C = 8 a V = 12. Preto je:

A = C + V - 2 = 8 + 12-2 = 18

Zväzok

Objem V akéhokoľvek hranolu, či už priamy alebo šikmý, pravidelných alebo nepravidelných tvárí, je daný:

V = základná plocha x výška

Preto budeme potrebovať vzorce pre oblasť, ktorú sme predtým videli.

Napríklad pre priamy hexagonálny hranol, ktorého základy sú pravidelnými šesťuholníkmi, je objem daný:

V = 2.5981.do².h

Odkazy

1. Matematika otvorená referencia. Polygón. Získané z: Mathpenref.com.
2. Wikipedia. Hranol. Obnovené z: je.Wikipedia.com.