Zásadný vzorec Archimedes, demonštrácia, aplikácie

On Archimedesov princíp Hovorí, že úplne alebo čiastočne ponorené telo dostáva vertikálnu silu zvanú TAM, čo je rovnocenné s hmotnosťou objemu kvapaliny vytlačenou telom. 

Niektoré predmety plávajú vo vode, iné klesajú a niektoré sa čiastočne ponoria. Na potopenie plážovej lopty je potrebné vyvinúť úsilie, pretože táto sila je okamžite vnímaná, ktorá sa ju snaží vrátiť na povrch. Namiesto toho sa kovová guľa rýchlo klesá. 

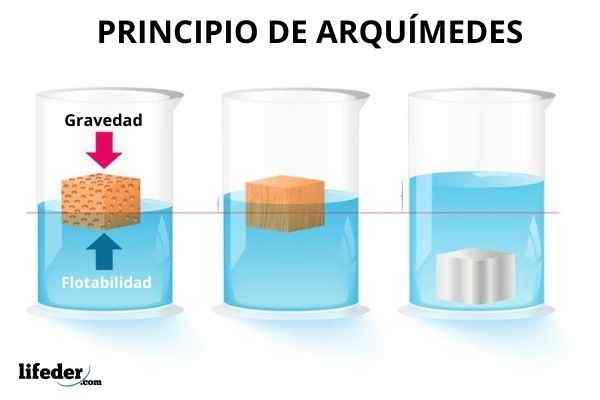
Na druhej strane, ponorené predmety sa zdajú byť ľahšie, preto existuje sila, ktorú vyvíja tekutina, ktorá je proti hmotnosti. Ale vždy nemôžete vôbec kompenzovať gravitácii. A hoci je to zrejmejšie pri vode, plyny sú tiež schopné vyrábať túto silu na ponorené predmety v nich.

[TOC]

História

Archimedes of Syrakúzy (287-212 a. C.) Bol to ten, kto musel objaviť tento princíp, ktorý bol jedným z najväčších vedcov v histórii. Hovorí sa, že kráľ Hierón II v Syrakúzach poslal zlatníka na výrobu novej koruny, za ktorú mu podal určité množstvo zlata.

Archimedes

Keď kráľ prijal novú korunu, mal správnu váhu, ale mal podozrenie, že ho zlatníctvo podviedol pridaním striebro namiesto zlata. Ako by som to mohol skontrolovať bez zničenia koruny?

Hierón nazval Archimedes, ktorého sláva bola dobre známa, aby mu pomohla vyriešiť problém. Legenda potvrdzuje, že Archimedes bol ponorený do vane, keď našiel odpoveď, a tak bola jeho emócia, že bežal nahý ulicami Syrakúz, aby hľadal kráľa kričiaceho „Eureka“, čo znamená „našiel som to“.

https: // giphy.com/gifs/stito3echtlnbvLiz3

Čo našli Archimedes? Pri vstupe do kúpeľne hladina vody vo vani, keď vstúpi,, čo znamená, že ponorené telo vytlačí určitý objem kvapaliny.

A ak som korunu ponoril do vody, musel som tiež presunúť určitý objem vody, ak bola koruna vyrobená zo zlata a iná, ak bola vyrobená zo zliatiny so strieborným strieborným.

Zásadný vzorec Archimedes

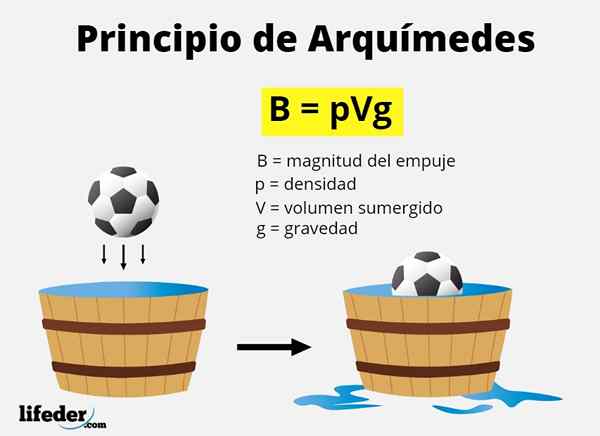
Propagačná sila uvedená v princípe Archimedes je známa ako TAM hydrostatický ani flotačná sila A, ako sme už povedali, je to ekvivalentné hmotnosti objemu tekutiny nahradenej telom, keď je ponorené.

Objem vytlačený je ekvivalentný objemu objektu, ktorý je ponorený, buď úplne alebo čiastočne. Pretože váha čohokoľvek je mg, A hmotnosť tekutiny je Hustota x, Popieranie toho, ako b do veľkosti ťahu, matematicky musí:

B = m_plynulý x g = hustota tekutiny x ponorená objem x gravitácia

B = ρ_plynulý x v_ponorený x g

Kde grécke písmeno ρ („rho“) označuje hustotu.

Zjavná váha

Hmotnosť objektov sa počíta dobre známym výrazom mg, Veci sa však cítia ľahšie, keď sú ponorené do vody. 

On zjavná váha objektu je to, čo má, keď je ponorený do vody alebo inej kvapaliny a pozná sa, môžete získať objem nepravidelného objektu, ako je korunka kráľa hieróna, ako bude vidieť nižšie.

Môže vám slúžiť: 13 príkladov Newtonovho prvého zákona v reálnom živote

Za týmto účelom je úplne ponorená do vody a podlieha lane pripevnené k a dynamometer -nástroj vybavený pružinou, ktorý slúži na meranie síl-. Čím väčšia je hmotnosť objektu, tým väčšie je predĺženie pružiny, ktoré sa meria na stupnici uvedenej v zariadení.

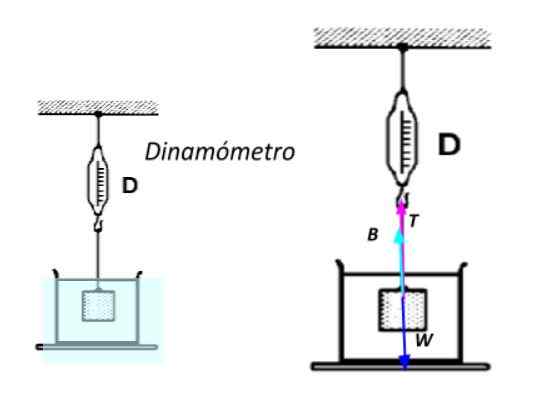Zjavná hmotnosť ponoreného objektu. Zdroj: Pripravený F. Zapata.

Uplatňovanie Newtonovho druhého zákona s vedomím, že objekt je v pokoji:

Σf_a = B + t - w = 0

Zjavná hmotnosť w_do Je to ekvivalentné napätiu na late T:

T = w_do

W_do = mg - ρ_plynulý . Vložka. g

Ak je potrebný ponorený zväzok V, vymaže sa ako:

V = (w - w_do ) / ρ_plynulý  . g

Demonštrácia

https: // giphy.com/gifs/mcphppgtnpbhl4cgaq

Keď sa telo ponorí, ťah je sila, ktorá je výsledkom všetkých síl, ktoré sa vyvíjajú na tele tlakom spôsobeným okolitou tekutinou:

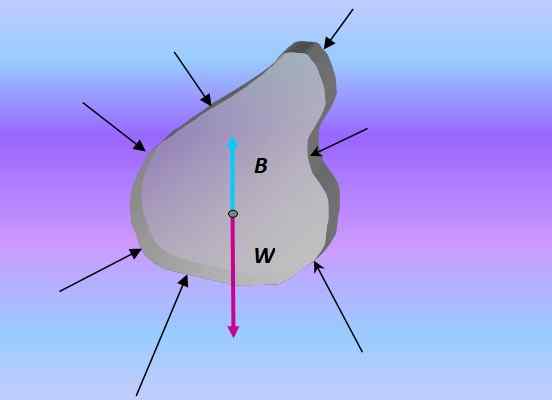Diagram voľného tela ponoreného predmetu. Zdroj: Pripravený F. Zapata.

Tlak a hĺbka

Pretože sa tlak zvyšuje s hĺbkou, výsledok týchto síl je vždy nasmerovaný vertikálne smerom nahor. Preto je princíp Archimedes dôsledkom základnej vety hydrostatického z ako:

P = ρ.g.z

Sily na statickej rovnováhe tekutiny

Na demonštráciu princípu Archimedes sa v pokoji odoberie malá valcová odpočinková časť, aby sa analyzovala sily, ktoré na ňu vyvíjajú, ako je to znázornené na nasledujúcom obrázku. Sily na zakrivenom povrchu valca sú navzájom rušivé. 

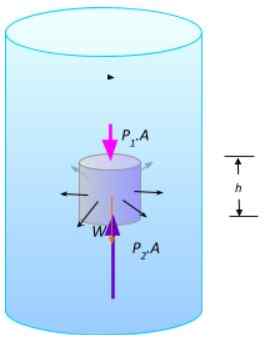Časť tekutiny v rovnováhe. Zdroj: Pripravený F. Zapata.

Veľkosti vertikálnych síl sú F₁ = P₁.A a F₂ = P2.A, existuje váha W. Keďže tekutina je v rovnováhe, musí byť zrušená súčet síl:

∑f_a = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Pretože ťah kompenzuje hmotnosť, pretože časť tekutiny je v pokoji, potom:

B = P₂.A- p₁.A = w

Z tohto výrazu vyplýva, že ťah je spôsobený rozdielom v tlakoch medzi hornou tvárou valca a dolnou časťou. Ako W = mg = ρplynulý. Vložka. g, Musíš:

B = ρ_plynulý. Vložka_ponorený. g

Čo je presne výraz pre ťah uvedený v predchádzajúcej časti.

Princípové aplikácie Archimedes

Balóny, ktoré plávajú: Princíp Archimedes v akcii

Princíp Archimedes sa objavuje v mnohých praktických aplikáciách, medzi ktorými môžeme pomenovať:

- Aerostatický balón. Čo tým, že má priemernú hustotu menšiu ako hustota okolitého vzduchu, pláva v ňom kvôli ťahovej sile.

- Lode. Prilba lode je ťažšia ako voda. Ale ak sa trup považuje za vzduch vo vnútri, kvocient medzi celkovou hmotnosťou a objemom je menší ako objem vody, a preto sa lode plávajú.

- Životné vesty. Keď sú postavené zo svetlých a pórovitých materiálov, sú schopné vznášať sa, pretože pomer hmotnostného objemu je menší ako voda.

- Plávajúce zatvorenie výplňového kohútika nádrže na vodu. Je to guľa plná vzduchu s veľkým objemom, ktorý pláva nad vodou, čo spôsobuje ťahovú silu - vynásobené efektom páky - uzatvára uzáver výplne vodného tanku, keď dosiahne celkovú úroveň.

Môže vám slúžiť: Unidimenzionálne vlny: matematický výraz a príklady

Príklady

Príklad 1

Legenda hovorí, že kráľ Hierón dal Goldsmithovi určité množstvo zlata, aby vytvoril korunu, ale nedôverčivý panovník si myslel, že zlatníctvo by sa mohol podvádzať pri umiestnení menej cenného kovu do koruny ako korunka. Ale ako som to mohol vedieť bez zničenia koruny? 

Kráľ objednal Archimedes a toto hľadanie riešenia objavil jeho slávny princíp.

Predpokladajme, že koruna váži vo vzduchu 2,10 kg-f a 1,95 kg-f, keď je úplne ponorená do vody. V tomto prípade nie je klam?

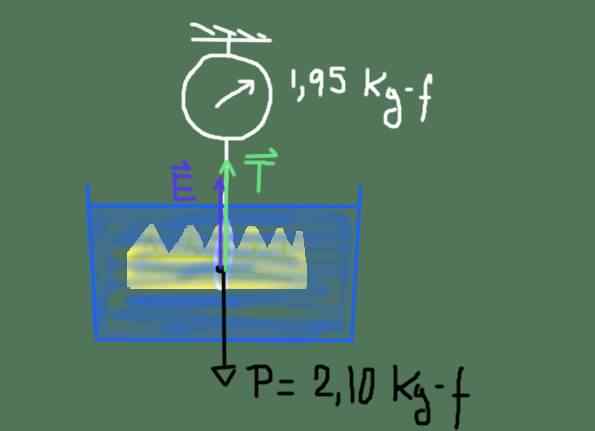Diagram tela bez koruny kráľa Herona. Zdroj: Pripravený F. Zapata

Schéma síl je znázornená na predchádzajúcom obrázku. Tieto sily sú: váha P z koruny, ťah A a napätie Tón lana, ktoré visí z mierky.

P = 2,10 kg-f a t = 1,95 kg-f je známe, je potrebné určiť veľkosť ťahu A:

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

Na druhej strane, podľa princípu Archimedes, je ťah rovnocenný s hmotnosťou vysťahovanej vody priestoru zaberanej korunou, to znamená hustota vody objemom koruny v dôsledku zrýchlenia gravitácie :

E = ρ_{vodná voda}⋅v⋅g = 1000 kg/m^3 ⋅ v ⋅ 9,8 m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Kde je možné vypočítať objem koruny:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Hustota koruny je kvocient medzi hmotnosťou koruny z vody a jej objemom:

Hustota koruny = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Hustota čistého zlata sa dá určiť podobným postupom a výsledkom je 19300 kg/m^3.

Porovnanie týchto dvoch hustoty je zrejmé, že koruna nie je čisté zlato! 

Príklad 2 

Na základe údajov a výsledku príkladu 1 je možné zistiť, koľko zlata bolo ukradnuté zlatom v prípade, že časť zlata bola nahradená striebrom, ktorý má hustotu 10500 kg/m^3 3.

Zavoláme ρc na hustotu koruny, ρo k hustote zlata a ρ_p na hustotu striebra.

Celková hmotnosť koruny je:

M = ρc⋅v = ρo⋅vo + ρ_p⋅vp

Celkový objem koruny je objem striebra plus objem zlata:

V = VO + VP ⇒ VP = V - VO

Výmena v hmotnostnej rovnici:

ρc⋅v = ρo⋅vo + ρ_p⋅ (v - vo) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

To znamená, že objem zlata, ktorý obsahuje korunu celkového objemu V, je:

VO = vlek (ρc - ρ_p)/(ρo - ρ_p) =…

… = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 m^3

Poznať váhu v zlate, ktorá obsahuje korunu, vynásobíme VO pre hustotu zlata:

Môže vám slúžiť: pravostranné pravidlo

MO = 19300 *0,00005966 = 1 1514 kg

Keďže hmotnosť koruny je 2,10 kg, vieme, že Goldsmith ukradol 0,94858 kg zlata a nahradil ho striebro.

Vyriešené cvičenia

Cvičenie 1

Obrovský héliový balón je schopný udržať v rovnováhe (bez toho, aby stúpal alebo zostupoval).

Predpokladajme, že hmotnosť osoby a košík, reťazce a balón je 70 kg. Aký je objem hélia potrebný na to, aby sa to stalo? Akú veľkosť bude mať balón?

Riešenie

Predpokladáme, že ťah sa vyrába hlavne objemom hélia a že ťah zvyšku komponentov je veľmi malý v porovnaní s héliom, ktorý zaberá oveľa väčší objem.

V tomto prípade bude potrebný objem hélia, ktorý je schopný poskytnúť ťah 70 kg +.

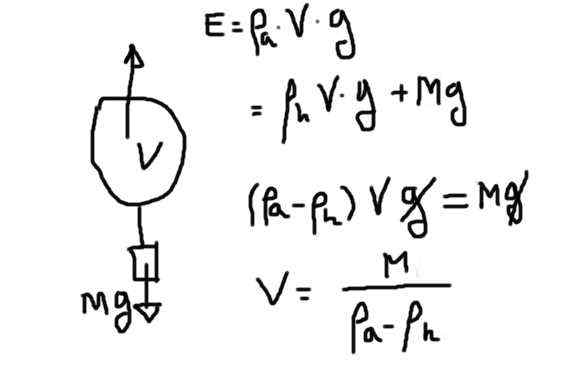Voľný telesný fdiaogram plný hélia. Zdroj: Pripravený F. Zapata.

Hluk je produktom objemu hélia v dôsledku hustoty hélia v dôsledku zrýchlenia gravitácie. Tento ťah musí kompenzovať hmotnosť hélia plus hmotnosť zvyšku.

DAHOK

kde sa dospelo k záveru, že v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

To znamená, že 65 je potrebných.4 m^3 hélia pri atmosférickom tlaku na podporu.

Ak predpokladáme sférický balón, nájdeme polomer z vzťahu medzi objemom a polomerom gule:

V = (4/3) ⋅π⋅r^3

Kde r = 2,49 m. Inými slovami, bude sa vyžadovať priemer 5 m plný hélia.

Cvičenie 2

Materiály s nižšou hustotou, ktoré voda vznáša rovnakým. Predpokladajme, že máte polystyrénové kocky (biele korok), drevo a ľad. Jeho hustoty v kg na meter kubický sú: 20, 450 a 915.

Zistite, aký zlomok celkového objemu je mimo vody a akú výšku vyniká, vzhľadom na povrch vody, ktorá sa berie ako hustota posledných 1 000 kilogramov na meter kubických.

Riešenie 

Plávajúca sa vyskytuje, keď sa telesná hmotnosť rovná ťahu v dôsledku vody:

E = m⋅g

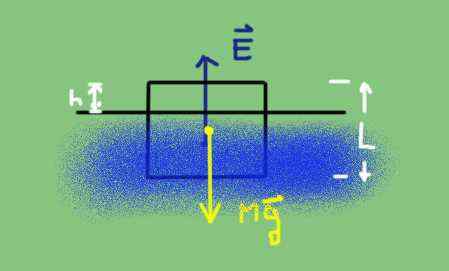Diagram voľného tela čiastočne ponoreného objektu. Zdroj: Pripravený F. Zapata.

Hmotnosť je hustota tela DC vynásobená jeho objemom V a zrýchlením gravitácie g.

Hluk je hmotnosť posunutej tekutiny podľa princípu Archimedes a je vypočítaná vynásobením hustoty D vody ponoreným objemom V 'a zrýchlením gravitácie.

To je:

D⋅v'⋅g = dc⋅v⋅g

Čo znamená, že ponorená objemová frakcia sa rovná kvocientu medzi hustotou tela a hustotou vody.

(V '/v) = (dc/d) 

To znamená, že vynikajúca frakcia objemu (v "/v) je

(V "/v) = 1 - (dc/d)

Jo h Je to vynikajúca výška a L Na strane kocky Frakcia hlasitosti môže byť napísaná ako

(H kedykoľvek, Inými slovami, vynikajúca výška je tiež

(h/l) = 1 - (dc/d)

Potom výsledky pre požadované materiály sú:

Polystyrén (biele korok):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% z vody

Drevo:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% z vody

Ľad:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% z vody

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Tekutina. Základy. Prvá edícia. McGraw Hill.
3. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 4. Tekutiny a termodynamika. Editoval Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Tekutina a hydraulická mechanika. McGraw Hill. 
5. Rex, a. 2011. Základy fyziky. Pearson. 239-263.
6. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. McGraw Hill.