Výpočet hmotnosti (fyzikálne), jednotky, príklady, cvičenia

On váha Je to sila, s ktorou Zem priťahuje predmety na jej povrch. Zakaždým, keď je predmet spadnutý, to ide na zem, nie je schopný vyliezť svojimi vlastnými prostriedkami, ani sa nedostane na polovicu, čo je preto, že ju priťahuje Zem.

Všetky objekty vždy priťahujú navzájom, dokonca aj tých najmenších, iba to, že veľkosť sily, s ktorou robia, je úmerná hmotnosti. To znamená, že predmety s malou hmotnosťou vyvíjajú malú silu nad ostatnými, ale nebeské telá, ako je Zem, sú schopné vyvíjať veľmi veľkú silu.

Zem udržiava okolo neho mesiac obiehať vďaka tejto sile príťažlivosti, ktorá sa volá Gravitačná príťažlivosť Pokiaľ ide o objekty, ktoré sú ďaleko od zemského povrchu, a váha Keď sú objekty blízko.

Z toho vyplýva, že gravitačná sila nevyžaduje, aby boli objekty nevyhnutne v kontakte, aby konali: preto sa hovorí, že ide o silu konania na diaľku.

Objekty majú stále váhu, aj keď sú v určitej výške na zemi a čím väčšie, tým väčšia bude táto váha.

Veľký anglický vedec Isaac Newton ako prvý, kto poskytol vysvetlenie tohto problému, prostredníctvom univerzálneho zákona o gravitačnej správe, ktorý nesie jeho meno a odvtedy slúžil na pochopenie toho, ako objekty interagujú s omšou s hmotnosťou. Je to veľmi dôležité, pretože akýkoľvek objekt na planéte má váhu.

[TOC]

Váh

Systém medzinárodných jednotiek, ak je hmotnosť hmotnosti Newton, pomenované na počesť Izáka Newtona. Toto je jednotka na meranie síl všetkého druhu.

Newton, skrátená N, je definovaná ako potrebná sila pre hmotný objekt 1 kg na získanie zrýchlenia 1 m/s². Okrem Newtonu existujú aj ďalšie jednotky sily bežného použitia, napríklad nasledujúce:

Kilogramová sila

On kilogramová sila o Kilopondio, skrátene KG-F alebo KP, hoci sa bežne nazýva kg bez ďalších. Je potrebné špecifikovať umiestnenie, pretože ako je uvedené, gravitačné pole prežíva variácie s výškou a zemepisnou šírkou.

Keď niekto povie, že váži 45 kg, v skutočnosti to znamená, že ich hmotnosť je 45 kg-f, pretože kilogram je jednotka vyhradená pre hmotnosť.

Môže vám slúžiť: Otvorený obvod

Rovnocennosť medzi kg-f a n je: 1 kg-f = 9.8 n

Librová sila

Ten Fuerza, Skrátene LB-F je tiež jednotka sily, ktorá je analogická kg-f, pretože je to sila, ktorú Zem vyvíja na objekt 1 lb hmotnosti. A ako v prípade KG-F, nie je problém s hodnotami, keď ste na Zemi, to znamená objekt hmotnosti, váži 1 lb-f-f-f-f-f-f.

Rovnocennosť v LB-F a N je: 1 lb-f ≡ 4,44822 n.

Výpočet a vzorec

Hmotnosť objektu je úmerná jeho hmotnosti. Väčšia hmotnosť, väčšia váha.

Vzorec na nájdenie rozsahu hmotnosti p (alebo tiež w, ako niekedy označuje, „Hmotnosť“ V angličtine) je to veľmi jednoduché:

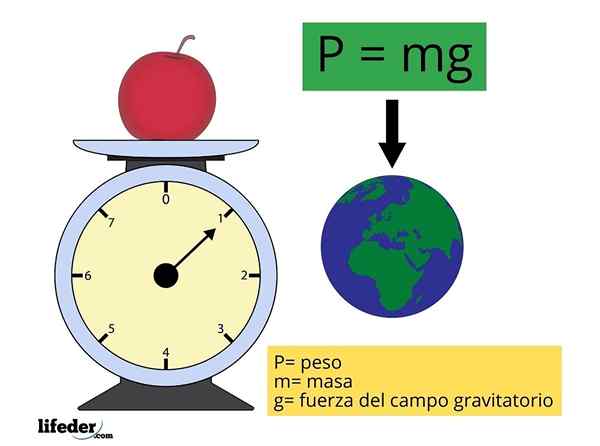
P = mg

Kde m predstavuje hmotnosť objektu a g Je to veľkosť zrýchlenia gravitácie (intenzita gravitačného poľa alebo závažnosť), približne konštantná a ktorej hodnota sa považuje za 9.81 m/s² Pre najčastejšie výpočty.

Hmotnosť je vektor a na rozlíšenie medzi vektorom a jeho veľkosťou sa používajú výrazné písmená. Týmto spôsobom, keď hovoríme o P, je zrejmé, že je to numerická hodnota a keď je napísaná P Odkazuje sa na vektor:

P = m ∙g

Ten g S odvážnymi textami je to pozemné gravitačné pole, to znamená vplyv, ktorý Zem vyvíja na priestor, ktorý ju obklopuje, bez ohľadu na to, či ho vníma iné telo alebo nie. Akýkoľvek objekt s hmotnosťou má svoje vlastné gravitačné pole, či už malý alebo veľký.

Intenzita pozemného gravitačného poľa g Nie je to úplne konštantné. Má malé variácie, ktoré vznikajú hlavne preto, že Zem nie je dokonalá guľa a tiež do miestnej výšky a rozdielov hustoty. Ale pre väčšinu aplikácií, hodnota 9.81 m/s² Funguje to veľmi dobre.

Ostatné nebeské telá majú svoje vlastné charakteristické gravitačné pole, preto sa zrýchlenie gravitácie líši podľa planéty alebo satelitu. Rovnaký objekt by mal v každej z nich inú váhu, a preto váha nie je charakteristickou vlastnosťou vecí, ale vo všeobecnosti predmetu.

Hmotnosť ako vektor

Hmotnosť je vektor, a preto má veľkosť, smer a význam. V blízkosti zemského povrchu je hmotnosť zvislý vektor a smer je vždy dole.

Všeobecne je vertikálna adresa vymenovaná za os a ani z, A význam je priradený znak + alebo znamenie - na rozlíšenie od smeru nahor. Výber závisí od umiestnenia pôvodu. Na dolnom obrázku bol pôvod zvolený v bode, z ktorého padá jablko:

Môže vám slúžiť: ideálny plyn: model, správanie, príklady Hmotnosť je vektor, ktorý je smerovaný vertikálne nadol. Zdroj: f. Zapata.

Jednotkový vektor J, Vektor s veľkosťou rovnocenného 1 sa používa na nasmerovanie a rozlíšenie vertikálneho smeru. Pokiaľ ide o tento vektor, hmotnosť je napísaná takto:

P = mg ( - J)

Kde je negatívny znak priradený k smeru.

Rozdiely medzi hmotnosťou, hmotnosťou a objemom

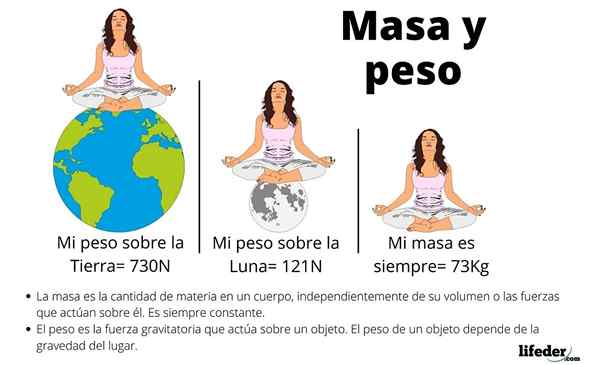
Tieto tri koncepty sú často zmätené, ale preskúmanie charakteristík hmotnosti je ľahké ju odlíšiť od hmotnosti a objemu.

Na začiatok závisí hmotnosť od gravitačného poľa miesta, kde je objekt. Napríklad na Zemi a na Mesiaci to isté má inú váhu, hoci množstvo atómov, ktoré ho tvoria, je konštantné.

Hmotnosť je skalárna veľkosť, ktorá súvisí s množstvom atómov, ktoré tvoria objekt a je svedcom odporu, že objekt musí zmeniť svoj pohyb, vlastnosť zvaná zotrvačnosť.

Pokiaľ ide o svoju časť, objem je miera priestoru obsadeného objektom, ďalšie skalárne množstvo. Dva objekty s rovnakým objemom vážia to isté, napríklad kocka železa váži oveľa viac ako iný polystyrén rovnakých rozmerov.

Súhrn:

• Hmotnosť súvisí s množstvom hmoty, ktorú má telo.
• Hmotnosť je sila vyvíjaná Zemou na túto hmotu, úmerná k nej.
• Objem je priestor obsadený hmotou.

Je potrebné poznamenať, že byť skalárnymi množstvami, ani hmotnosťou, ani objemom nemá smer alebo význam, ale iba číselnú hodnotu a primeranú jednotku. Na druhej strane, hmotnosť, ako vektor, musí byť vždy vyjadrená správne a poukazuje na veľkosť, jednotu, smer a význam, ako v predchádzajúcej časti.

Príklady hmotnosti

Všetky objekty na Zemi majú váhu, môžete dokonca „vážiť“ objekty, ktoré nie sú na Zemi, napríklad iné planéty alebo slnko, hoci nepriamymi prostriedkami, samozrejme, je to.

Keďže rozsah hmotnosti je veľmi veľký, používa sa vedecký zápis (v silách 10) na vyjadrenie niektorých, ktoré sú veľmi veľké alebo veľmi malé:

-Slnko: 1 989 × 10³⁰ kg-f

-Jupiter: 1 898 × ​​10²⁷ kg-f

-Komár: 2.0 × 10^-5 N

-Deti: 34.3 n

-Dieťa: 353 n

-Dospelá osoba: 65 kg-f

-Dospelý slon: 5.5 × 10³ kg-f

-Modrá veľryba: 1.0 × 10⁶ N

Cvičenie

Cesto 20 kg spočíva na stole.

a) Nájdite hmotnosť krabice a normálnu silu, ktorú na ňu tabuľka vyvíja.

Môže vám slúžiť: ochrana lineárnej hybnosti: princíp, príklady, cvičenia.

b) Ďalší 10 kg sa umiestni na prvý. Nájdite normálne, že tabuľka cvičí na škatuľke 20 kg a normálny, ktorý uplatňuje na najmenšiu políčku.

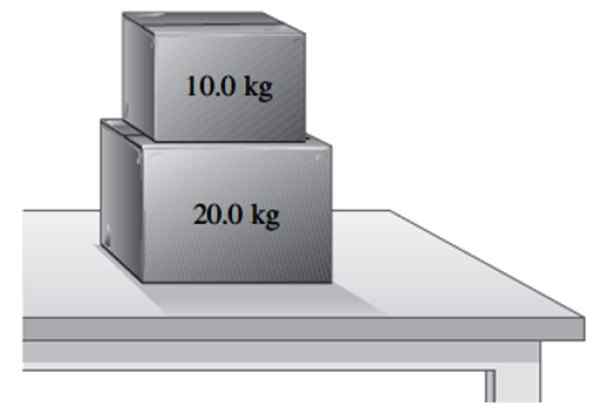Dve škatule spočívajúce na stole. Zdroj: f. Zapata.

Roztok

Je vhodné vytvoriť na krabici bezplatný diagram tela, ktorý spočíva v kreslení síl, ktoré na ňu pôsobia.

V tejto situácii je na vrchu stále najmenšia škatuľka, preto existujú iba dve sily: prvá je váha P ktorý sa nakreslí vertikálne nadol, ako je uvedené v predchádzajúcich úsekoch a potom je tu normálny N, čo je kolmá sila, ktorú tabuľka vyvíja a zabraňuje pádu krabice.

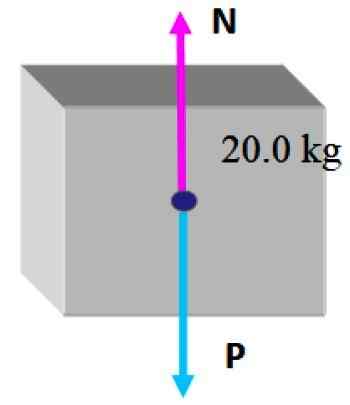
Pretože box je za týchto okolností v statickej rovnováhe, je rozumné dospieť k záveru, že veľkosť normálu je rovnaká ako váha, takže preto môže kompenzovať:

N = mg = 20.0 kg x 9.8 m/s² = 196 n; nasmerované vertikálne nahor.

Zvláštnosť je hmotnosť p = 196 n nasmerovaná vertikálne nadol.

Riešenie B

Teraz sa o oboch objektoch vyrábajú nové bezplatné diagramy tela. Pre veľké boxy sa veci trochu zmenia, pretože malá škatuľka na ňu vyvíja silu.

Sily sú nasledujúce: N a P Sú normálne, že stôl cvičí a hmotnosť na škatuli 20.0 kg, to sa nezmenilo. A nová sila, ktorú vyvíjala malá škatuľka, je N₁, Normálny kontakt s hornou tvárou veľkého boxu.

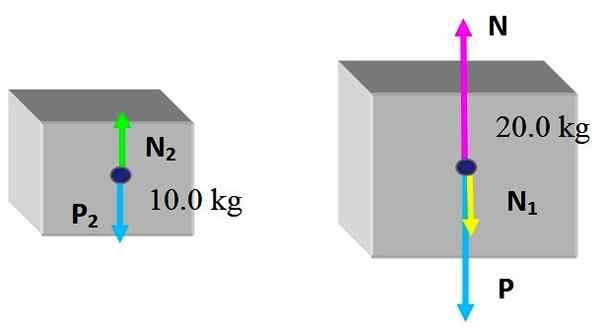
Pokiaľ ide o malú škatuľu, prijíma normálne N₂, uplatňovaná hornou tvárou veľkej škatule a samozrejme jej hmotnosť P₂. Pretože políčka sú statickým vyvážením:

N₂ - P₂ = 0

N - n₁ - P = 0

Z prvej rovnice musíte n₂ = P₂ = 10 kg x 9.8 m/s² = 98 n. Podľa zákona a reakcie je veľkosť sily, ktorú dostáva malá škatuľka, rovnaká ako na veľkú škatuľu, potom:

N₂ = N₁ = 98 n

Z druhej rovnice je normálne n, že sa stôl cvičí na veľkom škatuli, ktorý má naopak malú škatuľu na vrchu:

N = n₁ + P = 98 n + 196 n = 294 n

Odkazy

1. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
5. Serway, r., Jewett, J. 2008. Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
6. Thomas Griffith, w. 2007. Koncepčná fyzika. MC Graw Hill.