Obvod kruhu, ako ho dostať von a vzorce, vyriešené cvičenia

On obvod kruhu Je to súbor bodov, ktorý tvorí obrys kruhu a je tiež známy ako dĺžka obvodu. Závisí to od polomeru, pretože väčší obvod bude mať zjavne väčší obrys.

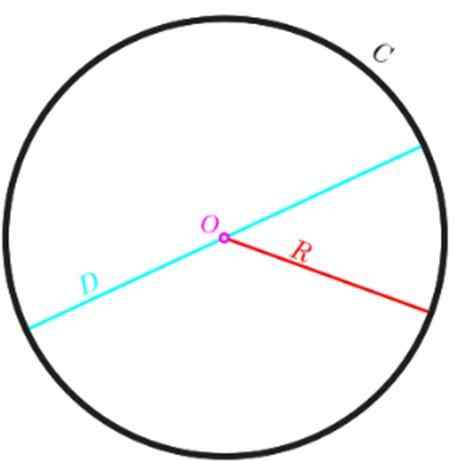
Byť P Obvod kruhu a R polomer toho istého, potom môžeme vypočítať P S nasledujúcou rovnicou:

P = 2π.R

Obvod kruhu (v tomto prípade pizza) závisí od jeho rádu. Zdroj: Pixabay.

Kde π je skutočné číslo (číta „pi“), ktoré má hodnotu približne 3.1416… Pozastavené body sú spôsobené skutočnosťou, že π má nekonečné desatinné miesta. Preto pri výpočtoch je potrebné zaokrúhliť svoju hodnotu.

Pre väčšinu aplikácií však stačí vziať tu uvedenú sumu alebo použiť všetky desatinné miesta, s ktorými kalkulačka funguje.

Ak namiesto polomeru je radšej používať priemer D, o ktorom vieme, že je dvakrát polomer, obvod je vyjadrený takto:

P = π.2R = π.D

Pretože obvod je dĺžka, musí sa vždy vyjadriť v jednotkách, ako sú merače, centimetre, nohy, palce a ďalšie, v závislosti od preferovaného systému.

[TOC]

Obvody a kruhy

Často sa používajú výrazne zameniteľne, to znamená ako synonymá. Ale stáva sa, že medzi nimi existujú rozdiely.

Slovo „obvod“ pochádza z gréckeho „obdobia“, čo znamená obrys a „metro“ alebo meranie. Obvod je obrys alebo obvod kruhu. Formálne je definované:

Obvod je súbor bodov s rovnakou vzdialenosťou k bodu nazývaného stred, a táto vzdialenosť je polomerom obvodu.

Pokiaľ ide o svoju časť, kruh je definovaný takto:

Kruh je súbor bodov, ktorých vzdialenosť k bodu nazývaného stred je menšia alebo rovná pevnej vzdialenosti nazývanej rádio.

Čitateľ môže varovať jemný rozdiel medzi oboma konceptmi. Obvod sa týka iba súboru okrajových bodov, zatiaľ čo kruh je súbor bodov od okraja do vnútra, ktorého obvodom je hranica.

Môže vám slúžiť: Cvičenia pre odbavenie vzorcov

Cvičenia dEmostrácia výpočtu obvodu kruhu

Prostredníctvom nasledujúcich cvičení sa opísané pojmy uvedú do praxe, ako aj niektoré ďalšie, ktoré sa budú vysvetliť tak, ako sa objavia. Začneme od najjednoduchšieho a stupeň obtiažnosti sa postupne zvýši.

- Cvičenie 1

Nájdite obvod a plochu rádiového kruhu 5 cm.

Riešenie

Rovnica uvedená na začiatku sa uplatňuje priamo:

P = 2π.R= 2π.5 cm = 10 π cm = 31.416 cm

Na výpočet oblasti Do Používa sa nasledujúci vzorec:

Do = π.R² = π. (5 cm)²= 25π cm²= 78.534 cm²

- Cvičenie 2

a) Nájdite obvod a plochu prázdnej oblasti nasledujúceho obrázku. Stred zatieneného kruhu je v červenom bode, zatiaľ čo stred bieleho obvodu je zelený bod.

b) Opakujte predchádzajúcu časť pre tieňovanú oblasť.

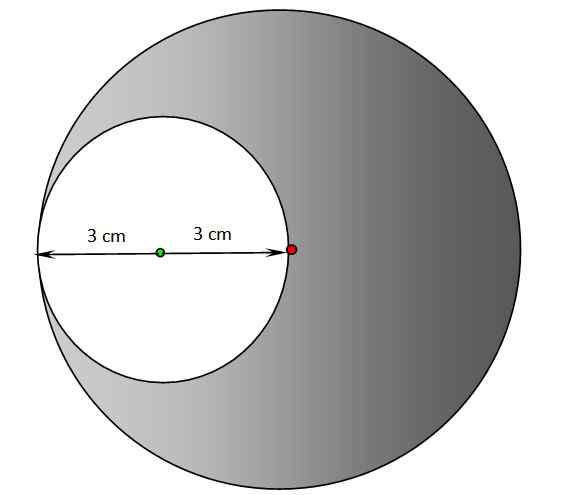Kruhy na cvičenie 2. Zdroj: f. Zapata.

Riešenie

a) Polomer bieleho obvodu je 3 cm, preto uplatňujeme rovnaké rovnice ako v cvičení 1:

P = 2π.R= 2π.3 cm = 6 π cm = 18.85 cm

Do = π.R² = π. (3 cm)²= 9π cm²= 28.27 cm²

b) Pre tieňovaný kruh je polomer 6 cm, jeho obvod je dvojnásobok vypočítaný v oddiele A):

P = 2π.R= 2π.6 cm = 12 π cm = 37.70 cm

A nakoniec sa oblasť tieňovanej oblasti vypočíta takto:

- Prvou je oblasť tieňovaného kruhu, akoby bola dokončená, čo budeme volať “, ako je tento:

Do ' = π.R²= π.(6 cm)² = 36π cm²= 113.10 cm²

- Potom do oblasti Do ' Oblasť bieleho kruhu sa odpočíta, predtým vypočítaná v oddiele A), týmto spôsobom sa získa požadovaná oblasť, ktorá bude označená jednoducho ako:

A = a ' - 28.27 cm² = 113.10-28.27 cm² = 84.83 cm²

- Cvičenie 3

Nájdite oblasť a obvod tieňovanej oblasti na nasledujúcom obrázku:

Môže vám slúžiť: doplnkové uhly: čo sú, výpočet, príklady, cvičenia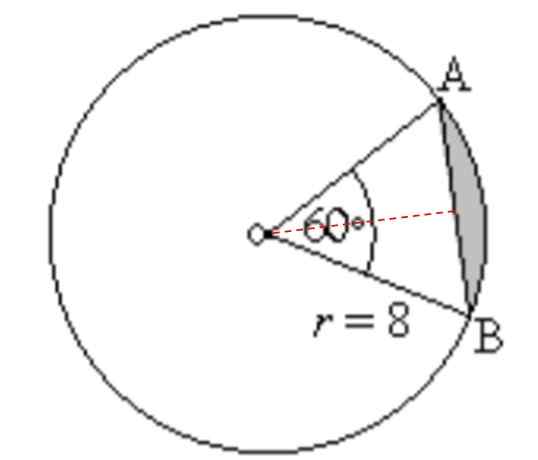Obrázok pre cvičenie 3. Zdroj: f. Zapata.

Riešenie

Výpočet oblasti tieňovanej oblasti

Najprv vypočítame oblasť Obežník alebo klin, medzi priamymi segmentmi OA a OB a segmentom kruhového AB, ako je to znázornené na nasledujúcom obrázku:

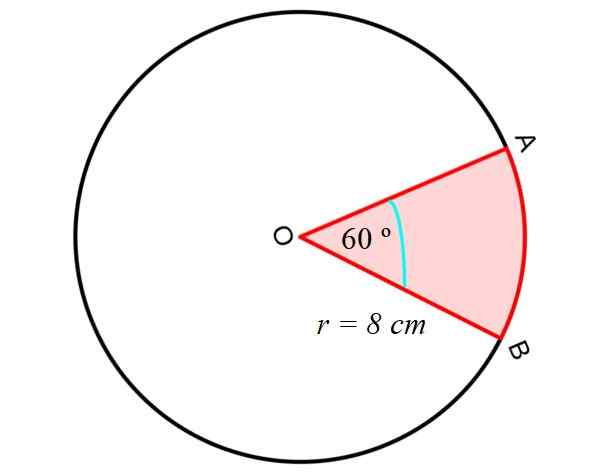
Na tento účel sa používa nasledujúca rovnica, ktorá nám dáva plochu kruhového sektora, poznanie polomeru R a centrálneho uhla medzi segmentmi OA a OB, to znamená dva rádiá obvodu:

Do _Obežník = Π.R². (aº/360 °)

Kde aº je centrálny uhol - je centrálny, pretože jeho vrchol je stredom obvodu - medzi dvoma rádiámi.

Krok 1: Výpočet oblasti obehového sektora

Týmto spôsobom je oblasť odvetvia znázornená na obrázku:

Do _Obežník = Π.R². (aº/360 °) = π. (8 cm)². (60 °/360 °) = (64/6) π cm²= 33.51 cm²

Krok 2: Výpočet oblasti trojuholníka

Potom vypočítame oblasť bieleho trojuholníka na obrázku 3. Tento trojuholník je rovnocenný a jeho oblasť je:

Do _trojuholník = (1/2) Výška základne x

Výška je bodkovaná červená čiara zobrazená na obrázku 4. Ak chcete nájsť, môžete napríklad použiť vetu Pythagoras. Ale nie je to jediný spôsob.

Čitateľ pozorovateľov si všimne, že rovnostranný trojuholník je rozdelený na dva rovnaké obdĺžniky, ktorých základňa je 4 cm:

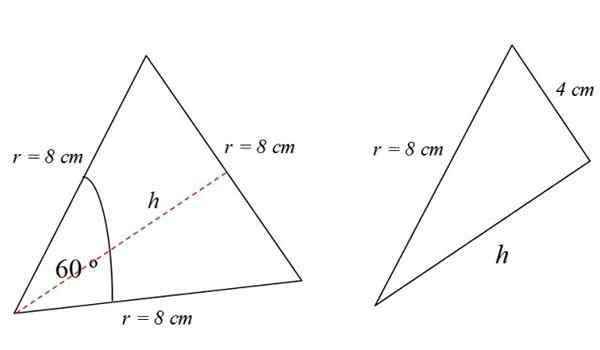
V pravom trojuholníku je pythagorská veta splnená, preto:

Pretože máte výšku trojuholníka, obdĺžniky a rovnostranná, jej oblasť sa vypočíta:

Do _trojuholník = (1/2) báza x výška = (1/2) 8 cm x 6.93 cm = 27.71 cm².

Krok 3: Výpočet tieňovanej oblasti

Stačí odpočítať hlavnú oblasť (oblasť kruhového sektora) menšej oblasti (rovnostranná trojuholník): a _{zatienená oblasť} = 33.51 cm² - 27.71 cm² = 5.80 cm².

Výpočet obvodu tieňovanej oblasti

Vyhľadaný obvod je súčet 8 cm priamočiarovej strany a obvodu obvodu AB.  Úplný obvod však podvádza 360 °, a preto oblúk, ktorý podvádza 60 °, je šiesty časť celej dĺžky, o ktorej vieme, že je 2.π.A:

Môže vám slúžiť: Rastúca funkcia: Ako ju identifikovať, príklady, cvičenia

AB = 2.π.R / 6 = 2.π.8 cm / 6 = 8.38 cm

Výmena obvodu tieňovanej oblasti je:

P = 8 cm + 8.38 cm = 16.38 cm.

Žiadosti

Obvod, rovnako ako oblasť, je veľmi dôležitým konceptom v geometrii as mnohými aplikáciami v každodennom živote.

Umelci, dizajnéri, architekti, inžinieri a mnoho ďalších ľudí využívajú obvod pri rozvíjaní svojej práce, najmä kruhu, pretože okrúhly tvar je všade: od reklamy, cez jedlo po strojové zariadenia.

Obvod a kruh patria medzi najpoužívanejšie geometrie. Zdroj: Pixabay.

Ak chcete poznať priamo dĺžku kruhu, stačí ho zabaliť závitom alebo reťazcom, potom natiahnite toto vlákno a zmerajte ho pomocou páskovej pásky. Druhou alternatívou je meranie polomeru alebo priemeru kruhu a použiť niektoré z vyššie uvedených vzorcov.

V každodennej práci sa koncept obvodu používa, keď:

-Vhodná forma sa vyberie pre určitú pizzu alebo veľkosť koláča.

-Mestská cesta bude navrhnutá výpočtom veľkosti redoma, kde sa autá môžu zmeniť na zmenu významu.

-Vieme, že Zem sa točí okolo slnka na približne kruhovej obežnej dráhe -v skutočnosti sú planétové dráhy eliptické, podľa Keplerových zákonov -ale obvod je veľmi dobrý prístup k väčšine planét.

-Primeraná veľkosť prsteňa alebo prsteňa, ktorý sa bude kupovať v internetovom obchode.

-Vyberieme kľúč k správnej veľkosti, aby sme uvoľnili orech.

A mnoho ďalších.

https: // youtu.Be/cr8xjryl5tk

Odkazy

1. Matematické návody zadarmo. Oblasť a obvod kalkulačky kruhu - geometrie. Obnovené z: AnalySemath.com.
2. Matematika otvorená referencia. Obvod, obvod kruhu. Získané z: Mathpenref.com.
3. Inštitút Monterey. Obvod a oblasť. Získané z: Montereyinstitute.orgán.
4. Vedecký. Ako nájsť obvod kruhu. Obnovené z: vedeckých.com.
5. Wikipedia. Obvod. Zdroj: In.Wikipedia.orgán.