Na čo sú čísla? 8 hlavných použití

Ten Čísla slúžia Pre nekonečno úloh na svete. Vo väčšine procesov sú objekty a miesta, ktoré sú zapojené čísla, aj keď nie vždy zrejmé. Jeho hlavným použitím je, že umožňujú počítať objekty.

Je ťažšie nájsť situácie, v ktorých sa čísla nezúčastňujú. Sú ústrednou súčasťou mnohých každodenných situácií života.

Napríklad trasy, ktoré sú roviny určené súradnicami Zeme, ktoré sú tvorené z čísel; To isté platí okrem iného pre lode a ponorky.

Hlavné použitie čísel

1- Počítajte objekty

Od detí, prvá vec, ktorá sa má naučiť robiť čísla, je počítať objekty, čo poskytuje ďalšie informácie v rôznych situáciách.

Napríklad na nasledujúcom obrázku sú dve skupiny jabĺk.

Obe skupiny obsahujú jablká. Ale keď sa hovorí, že v jednej skupine sú 3 jablká a v druhej skupine sú 2 jablká, je uvedený rozdiel medzi skupinami, čo je množstvo jabĺk v každej.

To by sa dalo urobiť povedať množstvu jabĺk, čo je možné vďaka číslam.

2- operácie algebraický

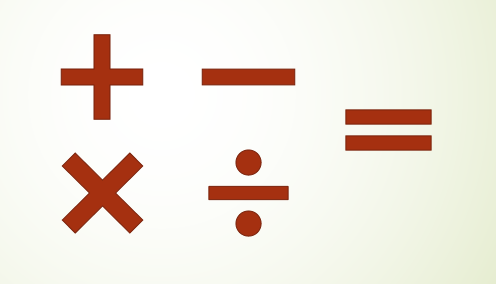
Po tom, čo sa naučil počítať, nasledujúce použitie čísel vyučovaných deťom súvisí s algebraickými operáciami, ako je súčet, odčítanie, násobenie a delenie.

Tieto štyri operácie sa používajú každý deň pre veľmi veľké množstvo ľudí, pričom je jednou z najbežnejších na pridanie, aby sa získala cena, ktorá sa má zaplatiť v supermarkete.

Môže vám slúžiť: horizontálna čiara

3- predstavuje hodnotu peňazí

Predtým, ako boli peniaze, ľudia robili výmeny alebo výmenné medzi predmetmi ich príslušnosti.

Potom boli zavedené peniaze, ktoré uľahčili tento typ postupov. Číslo, ktoré sa zobrazuje v každom lístku alebo mene.

Aby ste vedeli, koľko hodnoty má lístok, stačí vidieť číslo, ktoré má; to znamená množstvo peňažných jednotiek, ktoré predstavuje.

4- Identifikujte objekty

Čísla tiež pomáhajú identifikovať objekty. Napríklad na nasledujúcom obrázku sú zobrazené dva autobusy.

Jediný rozdiel, ktorý majú, je ich identifikačná doska, ktorá má čísla.

Vďaka číslam bude majiteľ každého autobusu vedieť, ktorý je váš. To isté sa stáva napríklad s dokumentmi identity ľudí.

5 binárne čísla

Veľmi časté, ale nie veľmi zjavné použitie je použitie binárnych čísel. Binárne čísla sú zastúpené iba pomocou nulov a niektorých.

Napríklad číslo 16 v binárnych číslach je číslo 10000.

Binárne čísla sa používajú vo svete výpočtov. Dáta zaobchádzané s počítačmi interne predstavujú nuly a niektoré, pretože pracujú s dvoma úrovňami napätia.

Ak chce počítač odoslať skutočnosť, tieto údaje sú reprezentované binárnym kódom, v ktorom nula predstavuje úroveň napätia a jeden predstavuje druhú úroveň napätia.

6- Zmerajte

Na meranie dĺžky objektu sa čísla používajú okrem jednotky merania (merače, míle).

Môže vám slúžiť: Aké sú trojuholníkové čísla? Vlastnosti a demonštrácie

To isté sa stane, keď chcete poznať hmotnosť objektu alebo tlak vzduchu, ktorý môže podporovať gumu na bicykli.

7- predstavujú vzdialenosti

Čísla slúžili na univerzalizáciu vzdialeností, či už v metrických dĺžkach alebo kilometroch anglo -saxonského systému. A v staroveku mala každá civilizácia svoj vlastný spôsob výpočtu vzdialenosti, a to väčšinou veľmi nepresné a subjektívne.

V skutočnosti je stále možné nájsť ľudí, ktorí, keď sa pýtajú, ako ďaleko je miesto, reagujú na „čo berie cigaru“, čo dáva jednotke času ako reprezentáciu vzdialenosti a nie dĺžky. 

8- Objednajte si ulice

Čísla sú medzinárodným spôsobom, ako lokalizovať každý dom, stavbu, miestne alebo inštitúciu, pretože sa nachádza na ulici a s číslom. 

Napríklad v Španielsku sú ulice uvedené kolegami a nepárnymi. Byť domami chodníka očíslovaný s rovesníkmi (2,4,6,8,10 ...) a domami druhej chodníka na tej istej ulici s nepárnymi číslami (1,3,5,7,9 ...). Človek z Madridu tak môže žiť na ulici Nicasio Gallego č. 9.

Odkazy

1. Barker, L. (2011). Vyrovnané texty pre matematiku: Číslo a operácie. Učiteľ vytvoril materiály.
2. Burton, m., Francúzština, c., & Jones, T. (2011). Používame čísla. Benchmark vzdelávacia spoločnosť.
3. Doudna, k. (2010). Keď používame čísla, nikto neporazí! Vydavateľstvo Abdo.
4. Fernández, J. M. (Devätnásť deväťdesiat šiestich). Projekt prístupu chemických dlhopisov. Reverzný.
5. Hernández, J. d. (s.F.). Notebook matematiky. Prah.
6. Lahora, m. C. (1992). Matematické aktivity s deťmi od 0 do 6 rokov. Vydania Narcea.
7. Marín, e. (1991). Španielska gramatika. Redakčný progreso.
8. Tocci, r. J., & Widmer, n. Siež. (2003). Digitálne systémy: princípy a aplikácie. Pearson Vzdelanie.

Môže vám slúžiť: 3 druhý druhý koreň (ľahké riešenie a vysvetlenie)