Jednorozmerné vlny matematického výrazu a príklady

Ten Jednosmerné vlny Sú to tí, ktorí sa šíria jedným smerom bez ohľadu na to, či dochádza k vibráciám alebo nie v rovnakom smere šírenia. Dobrým príkladom je vlna, ktorá sa pohybuje pozdĺž napätého lana, ako je vlna gitary.

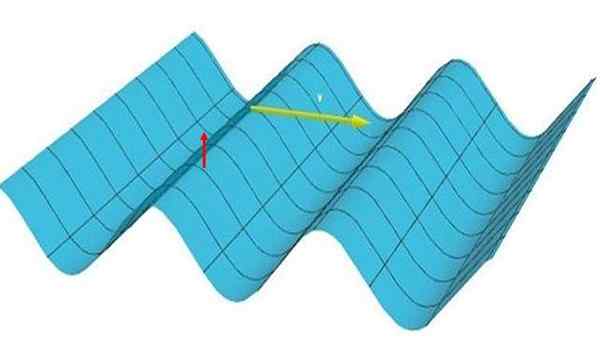
V plochej vlne krížiť, Častice vibrujú vertikálne (stúpajú a idú dolu, vidia červenú šípku na obrázku 1), ale je to jedno rozmerové, pretože rušenie prechádza jedným smerom a sleduje žltú šípku.

Obrázok 1: Obrázok predstavuje jednosmernú vlnu. Všimnite si, že hrebene a údolia tvoria rovnobežné čiary medzi sebou a kolmé na smer šírenia. Zdroj: Self Made.

Jednorozmerné vlny sa objavujú pomerne často v každodennom živote. Nasledujúca časť popisuje niektoré príklady z nich a tiež vlny, ktoré nie sú jednorozmerné, aby sa jasne stanovili rozdiely.

[TOC]

Príklady jednorozmerných vĺn a nenidimenzionálnych vĺn

Jednosmerné vlny

Toto je niekoľko príkladov jednej rozmerovej vlny, ktoré je možné ľahko pozorovať:

- Zvukový pulz, ktorý prechádza priamou tyčou, pretože je to narušenie, ktoré sa šíri po celom tyči.

- Vlna, ktorá prechádza vodným kanálom, aj keď posunutie hladiny vody nie je rovnobežné s kanálom.

- Vlny, ktoré sa šíria na povrchu alebo cez trojrozmerný priestor.

Nedimenzionálne vlny

Príklad nedimenzionálnej vlny sa nachádza vo vlnách, ktoré sú tvorené na povrchu pokojnej vody, keď je kameň spustený. Je to dvojrozmerná vlna predná valcovitá vlna.

Môže vám slúžiť: páková rukaObrázok 2. Obrázok predstavuje príklad toho, čo nie je jednosmerná vlna. Všimnite si, že hrebene a doliny tvoria kruhy a smer šírenia je radiálny smer smerom von, potom je to dvojrozmerná kruhová vlna kruhovej vlny. Zdroj: Pixabay.

Ďalším príkladom nečlennej dimenzionálnej vlny je zvuková vlna, ktorá generuje žabku výbuchom v určitej výške. Toto je trojrozmerná vlna s sférickými vlnami.

Matematické vyjadrenie jednej rozmerovej vlny

Najbežnejším spôsobom vyjadrenia jednosmernej vlny, ktorá sa šíri bez útlmu v pozitívnom smere osi X a rýchlosťou vložka Je to matematicky:

a (x, t) = f (x - v.t)

V tomto výraze a predstavuje narušenie v polohe X Okamžite tón. Tvar vlny je daný funkciou F. Napríklad vlnová funkcia znázornená na obrázku 1 je:  a (x, t) = cos (x - v t) a obraz vlny zodpovedá okamihu t = 0.

Vlna, ako je táto, opísaná funkciou kosínutia alebo sínusu, sa nazýva harmonická vlna. Aj keď to nie je jediný priebeh, ktorý existuje, je nanajvýš dôležitý, pretože akákoľvek iná vlna môže byť reprezentovaná ako prekrývanie alebo súčet harmonických vĺn. Je to známa Fourierova veta, tak sa používa na opis signálov všetkého druhu.

Keď vlna cestuje v zápornom smere osi x, jednoducho sa zmení vložka podľa -vložka Argument, bytosť:

a (x, t) = g (x + v t)

Obrázok 3 zobrazuje animáciu vlny, ktorá prechádza doľava: Je to forma nazývaná funkcia Lorentziana a jej Matematický výraz je:

Môže vám slúžiť: práca: vzorec, jednotky, príklady, cvičenia

a (x, t) = 1 / (1 + (x + 1⋅t)²

V tomto príklade je rýchlosť šírenia v = 1, -jednotka priestoru pre každú časovú jednotku-.

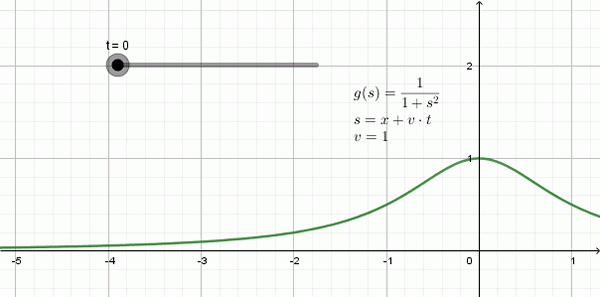Obrázok 3. Príklad Lorentziánskej vlny, ktorá rýchlo prechádza doľava v = 1. Zdroj: Pripravený F. Zapata s geogebou.

Jednosmerná vlnová rovnica

Vlnová rovnica je rovnica v čiastočných derivátoch, ktorých riešením je samozrejme vlna. Vytvára matematický vzťah medzi priestorovou časťou a jej časovou časťou a má formu:

Riešenie, ktoré je presne funkciou y (x, t), sa dá overiť výmenou a vývojom v tejto rovnici. Napríklad funkcie f (x - v t)  a  G (x + vt)  uvedené, sú to riešenia vlny rovníc.

Vyriešený príklad

Potom máte všeobecný výraz y (x, t) pre harmonickú vlnu:

a (x, t) = a⋅cos (k⋅x ± Ω⋅t + θo)

a) Opíšte fyzický význam parametrov A, k, Ω a θo.

b) Aký význam majú príznaky ± na argument coseno?

c) overte, či daný výraz je skutočne riešením vlnovej rovnice predchádzajúcej časti a nájdite rýchlosť vložka propagácia.

Riešenie do)

Vlastnosti vlny sú v nasledujúcich parametroch:

-Do predstavuje amplitúda alebo „výška vlny“.

-K je v Vlna A súvisí s vlnovou dĺžkou λ cez K = 2π/ λ.

-Ω Je to fuhlová expanzia A súvisí s obdobie Tón kmita

Ω = 2π/ t.

-θo Je to počiatočná fáza, čo súvisí s východiskovým bodom vlny.

Môže vám slúžiť: statické trenie: koeficient, napríklad cvičenie

Riešenie b)

Negatívny znak sa urobí, ak vlna prechádza pozitívnym smerom osi x a kladným znakom inak.

Riešenie c)

Overte, či daný výraz je riešením vlnovej rovnice je jednoduché: odoberie sa čiastočný derivát funkcie a (x, t) Pokiaľ ide o X dvakrát, je čiastočne odvodený od T dvakrát a potom sa oba výsledky stretnú, aby sa získala rovnosť:

Druhý odvodený od x: ∂²a/ ∂x²= -K². Do⋅cos (k⋅x ± Ω⋅t + θo)

Druhý odvodený od T: ∂²a/ ∂t²= -Ω². Do⋅cos (k⋅x ± Ω⋅t + θo)

Tieto výsledky sa nahradia vo vlnovej rovnici:

 -klimatizovať². Do⋅cos (k⋅x ± Ω⋅t + 9o) = (1/v²) (-Ω². Do⋅cos (k⋅x ± Ω⋅t + 9o))

Tak veľa Do Keď sa kosínus zjednoduší, pretože sa objavujú na oboch stranách rovnosti a argument kosínu je rovnaký, preto sa výraz zredukuje na:

-klimatizovať² = (1/v²) (-Ω²)

To umožňuje získať rovnicu vložka v zmysle Ω a klimatizovať:

vložka² = Ω² / k²

v = ± Ω / k

Odkazy

1. Elektronický vzdelávanie. Rovnica jednorozmerných harmonických vĺn. Získané z: e-duplikácie.Cathedu.je
2. Rincón fyziky. Vlny. Zdroj: fyzika.Blog.com.
3. Figueroa, D. 2006. Vlny a kvantová fyzika. Séria: Fyzika pre vedu a inžinierstvo. Editoval Douglas Figueroa. Univerzita Simon Bolivar. Caracas Venezuela.
4. Laboratórium fyziky. Vlnový pohyb. Získané z: Fisicalab.com.
5. Peirce, a. Prednáška 21: Rovnica jednorozmernej vlny: riešenie D'Alemberta. Zdroj: UBC.Ac.
6. Vlnová rovnica. Zdroj: In.Wikipedia.com