Tri -rozmerové vlny Koncept, typy a príklady

Byť tri rozmerové vlny Tie, ktoré sa šíria vo vesmíre, napríklad zvuková vlna, ktorú produkuje reproduktor. Táto vlna sa šíri vo všetkých smeroch, aj keď nie s rovnakou intenzitou vo všetkých z nich.

Ak dôjde k narušeniu v jednom bode priestoru, potom sa šíri v troch priestorových smeroch, čím sa predné čelné vlny zatvoria, sférické, eliptické alebo iné typ.

Tri rozmerové vlny produkované reproduktorom

Na druhej strane, ak miesto, kde vlny pochádzajú, to znamená, že zdroj má ploché rozdelenie, potom narušenie sa bude pohybovať hlavne v smere kolmom na túto rovinu a tvoria čelné čelné čely vlny.

[TOC]

Typy troch rozmerových vĺn

V troch rozmeroch vlny sú čelné čely súpravy povrchov ponorených do troch rozmerov.

Teraz je predná vlna geometrickým miestom vesmírnych bodov, ktoré sa dosahujú počiatočným narušením, súčasne v rovnakom čase.

Podľa symetrie prednej vlny: Ploché vlny, valcové vlny a sférické vlny a sférické vlny a sférické vlny sa zvyčajne uvažujú o tri typy vĺn, ktoré cestujú v trojrozmernom priestore. Skutočné vlny však nie vždy patria k týmto typom, pretože nemajú taký vysoký stupeň symetrie.

Ploché vlny

Plochá vlna, ktorá sa pohybuje v pozitívnom smere X rýchlo, je funkčne znázornená ako:

G (x, t) = f (x - v⋅t)

Táto vlna sa neobmedzuje iba na os X, ale tiež rozširuje adresy a a z. Ale funkčná forma naznačuje, že všetky body, ktoré majú rovnakú súradnicu X, bez ohľadu na súradnice (z, y), majú rovnakú hodnotu g.

V tomto prípade sú čelné čely roviny rovnobežné s rovinou Z-and, ktoré rýchlo postupujú vložka, To znamená, že plochá vlna zaberá všetky tri rozmerové priestory.

Výraz, ktorý predstavuje plochú vlnu, ktorá sa šíri v ľubovoľnom smere alebo rýchlo vložka, kde alebo Predstavuje jednotkových starších vektorových riaditeľov cos (a), cos (p) a cos (γ), je:

Môže vám slúžiť: reakčná entalpia: Definícia, termochémia, cvičenia

g = f (û • r - v kedykoľvek

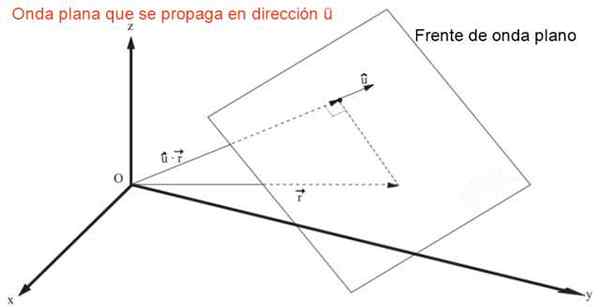Plochý vlnový vlny, ktoré sa šíri v trojrozmernom priestore rýchlo v. Zdroj: f. Zapata.

Priamou substitúciou je ľahké preukázať, že predchádzajúca expresia je riešením trojrozmernej vlny rovnice, rovnice v čiastočných derivátoch druhého lineárneho poriadku:

∂_XxG + ∂_RizornýG + ∂_ZZG = (1/v²) ∂_Ttg

Predchádzajúcu rovnicu je možné napísať kompaktnejšie pomocou laplaciánskeho operátora ∇²:

∇²G = (1/v²) ∂_Ttg

Valcové vlny

Keď je počiatočné narušenie distribuované po priamke, potom sa vlna šíri v radiálnom smere kolmom na túto čiaru a vyplňuje trojrozmerný priestor, ktorý ho obklopuje, s valcovitou vlnovou čelnou vlnou.

Sférické vlny

Ak je zdroj presný a médium, v ktorom sa šíri trojrozmerná vlna.

V prípade sférickej vlny, v ktorej je intenzita vlny identická vo všetkých smeroch, funkcia, ktorá opisuje narušenie, závisí iba od vzdialenosti r na včasný a časový zdroj tón.

V tomto prípade je zodpovedajúci laplacian:

∇²G = (1/r²) ∂_r(r² ∂_rg)

Byť vlnovou rovnicou:

∇²G = (1/v²) ∂_Ttg

Všeobecné riešenie by bolo:

g (r, t) = (1/r) f (r - v⋅t) + (1/r) g (r + v⋅t)

V tomto prípade sa hovorí, že je to sférická vlna. Ale môžu existovať varianty, ako bude vidieť nižšie

Neisotropné sférické vlny

Môže sa tiež stať, že sférická vlna, tj s vlnovými frontami tvorenými koncentrickými guľami do centrálneho bodu, je amplitúda alebo intenzita vlny iná v rôznych smeroch.

To sa stane, keď je centrálny zdroj vlny efektívnejší v smere ako ostatní. 

Môže vám slúžiť: fyzika pred Grékmi (Antigua Grécko)

Napríklad zvuk produkovaný rohom nemá všade rovnakú intenzitu, dokonca ani v prípade rohových bodov.

Intenzita nie je rovnaká, aj keď signál trvá rovnaký čas, kým sa tieto body dostanú. Je to sférická vlna, ktorá má nepodstatný smerový vzor. 

Existujú tiež sférické vlny v prípade elektromagnetických vĺn vytvorených anténou, ale nemusia byť rovnako intenzívne vo všetkých smeroch.

Anténa vysielača

Nehomogénna polovica

Ak médium nie je homogénne, potom je rýchlosť šírenia vlny odlišná v rôznych smeroch.

Príkladom nehomogénneho média je atmosféra, v ktorej sú tlakové rozdiely s výškou a existujú teplotné gradienty. Ďalším príkladom sú vrstvy zemskej kôry, ktorá sa líši v hustote a elastickom module. 

Nehomogenita má za následok vlnové fronty pochádzajúce z centrálneho presného zdroja nie sú koncentrické gule, pretože vzdialenosť prevezená vlnou v rovnakom časovom období je v každom smere odlišná.

Potom je tu trojrozmerná vlna, ktorej predná vlna nie je sférická.

Intenzita a energia sférickej vlny

Môžeme napísať vyjadrenie sférickej harmonickej vlny, ako je táto:

g (r, t) = (g_ani / r) cos (k⋅r - Ω⋅t)

Kde sa vlnové fronty šíria rýchlo rovnajúce sa:

V = Ω/k

A jeho amplitúda klesá s inverznou vzdialenosťou r presného zdroja sférických vĺn.

Harmonické vlny majú hustota energie (Energia na jednotku objemu) ε daná:

ε = ½ ρ Ω² (g_ani / r)²

V tejto rovnici:

-ρ Má jednotky hmotnosti na jednotku objemu a predstavuje hustotu média, kde sa šíri zvuková vlna.

-g_ani Je to amplitúda posunu prvku média, napríklad tekutiny, v dôsledku šírenia vlny.

Môže vám slúžiť: viskózne trenie (sila): koeficient a príklady

Malo by sa poznamenať, že keďže je to sférická vlna, hustota energie klesá s inverziou štvorca vzdialenosti.

Intenzita vlny, to znamená, že energia vysielaná na jednotku času je:

I = vrk

Ako vždy, v praxi je najdôležitejšou veľkosťou prenášanú na jednotku plochy do radiálnej vzdialenosti r:

P = v⋅ε = i_ani / r²

Bytosť Jo_ani = ½ ρ v Ω² g_ani².

Celková energia prenášaná na jednotku času cez polomer R je:  P zajtra²= 4π⋅i_ani, A ako sa očakávalo, nezávisí to od radiálnej vzdialenosti. 

Príklady troch rozmerových vĺn

Tri -dimenzionálne vlny sú veľmi časté, takže máme:

Elektromagnetické emitorové antény

Vlny produkované anténou alebo zvukom produkovaným hmatníkom sú trojrozmerné vlny, hoci rôznej povahy

Pokrývajú veľmi široké spektrum, od rádiových vĺn medzi stovkami kHz a stoviek MHz, až po vlny emitované anténou antény Wifi Rádu GHZ, ktorý už spadá do rozsahu mikrovlniek. 

Vieme, že mikrovlnná rúra, aj keď nie sú ionizujúcim žiarením, sú schopní zvýšiť teplotu organizmu, pretože obsahuje veľa vody.

Preto nie je vhodné mať Wi-Fi anténu blízko hlavy alebo tela. Stačí sa trochu preč, pretože v dvojnásobnej vzdialenosti je intenzita štvrtina.

Seizmické vlny

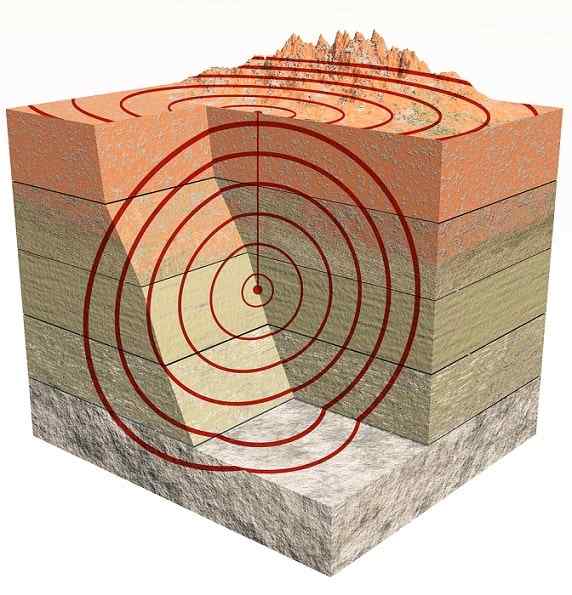Seizmické vlny

Sú to tiež tri rozmerové vlny. Hlavne existujú tie typu P ktoré sú kompresné vlny a typy Siež Čo sú rezanie alebo strih (sPočuť v angličtine).

Vlny P alebo primárne sú prví, ktorí dorazia, pretože sa šíria rýchlejšie ako vlny Siež alebo sekundárny.

Znieť

Zvuk hovoriť

Zvuk je trojrozmerný typ vlny. Tieto vlny sa šíria vo všetkých smeroch, aj keď, ako sme už povedali, nie s rovnakou intenzitou vo všetkých smeroch.

Je to preto, že zdroj zvuku nie vždy emituje s dokonale sférickou symetriou.

Odkazy

1. Barane, L. 1969. Akustika. Druhý. Vydanie. McGraw Hill.
2. Griffiths G. Lineárne a nelineárne vlny. Zotavené z: Scholarpedia.orgán.
3. Nottoli, h. 2004. Fyzika aplikovaná na architektúru. Nobuko.
4. Whitham g.B. 1999. Lineárne a nelineárne vlny. Mravný. 
5. Wikiwaves. Nelineárne vlny. Získané z: wikiwaves.orgán