Stacionárne vzorce vlny, charakteristiky, typy, príklady

Ten stojace vlny Sú to vlny, ktoré sa šíria v obmedzenej polovici, idú a prichádzajú do časti priestoru, na rozdiel od cestovných vĺn, ktoré sa pri šírení odchodu od zdroja, ktorý ich vznikol, a nevracia sa k nemu.

Sú základom zvukov vyrobených v hudobných nástrojoch, pretože sa ľahko objavujú na pevných reťazcoch, buď na jednom z jeho koncov alebo oboch. Vytvárajú sa tiež v napätých membránach, ako sú bubny alebo vnútorné trubice a štruktúry, ako sú mosty a budovy.

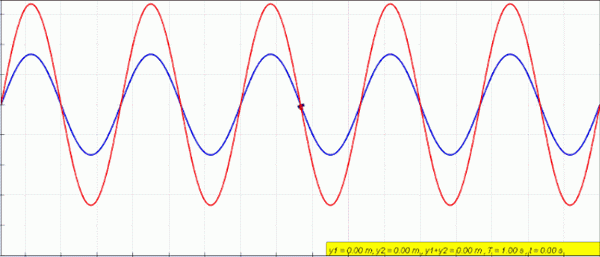Animácia stacionárnej (červenej) vlny vytvorenej superpozíciou ľavej (modrej) a pravej vlny (zelená). Zdroj: Lookangmany Vďaka autorovi pôvodnej simulácie = Wolfgang Christian a Francisco Schembre Autor knihy Easy Java Simulation = Francisco Schembre/CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/4.0)

Ak máte pevné lano na oboch koncoch, napríklad gitaru, napríklad vlny sa vytvárajú s rovnakou amplitúdou a frekvenciou, ktoré cestujú v opačných zmysloch a kombinujú výrobu javu zvaného nazývaného zasahovanie.

Ak sú vlny vo fáze, hrebene a údolia sú zarovnané a vedú k vlnu s dvojitou amplitúdou. V takom prípade sa hovorí o konštruktívnom zasahovaní.

Ale ak vlny, ktoré interferujú, sú mimo fázy, hrebene jedného spĺňajú doliny ostatných a amplitúda, ktorá je výsledkom, je nula. Potom je to deštruktívne rušenie.

[TOC]

Vzorce a rovnice

Hlavnými prvkami vlny, ktoré ju reprezentujú vo vesmíre a čase, sú jej amplitúda A, jej vlnová dĺžka λ a jej uhlová frekvencia Ω.

Prvky vlny. Zdroj: Wikimedia Commons.

V matematickej reprezentácii je uprednostňované používať k, ako Vlna o Čím sa vlna na jednotku deje. Preto je definovaný dĺžkou vlny λ, ktorá je vzdialenosťou medzi dvoma údoliami alebo dvoma hrebentami:

K = 2π/ λ

Kým uhlová frekvencia Súvisí s obdobím alebo trvaním úplnej oscilácie, napríklad:

Ω = 2π/ t

A tiež frekvencia F je daná:

F = Ω / 2π

Preto:

F = 1/t

Okrem toho sa vlny pohybujú rýchlosťou vložka podľa:

v = λ.F

Matematické vyjadrenie stacionárnej vlny

Matematicky môžeme vyjadriť vlnu prostredníctvom sínusovej funkcie alebo funkcie kosínutia. Predpokladajme, že existujú vlny rovnakej amplitúdy A, vlnovej dĺžky λ a frekvencie Ω, šíria sa pozdĺž lana a v opačných zmysloch:

a₁ = Hriech (kx - ωt)

a₂ = Hriech (kx + Ωt)

Pri ich pridaní nájdeme výslednú vlnu a_R:

a_R = y₁ + a₂ = Sen (kx - ωt) + sin (kx + ωt)

Existuje trigonometrická identita na nájdenie súčtu:

Môže vám slúžiť: čo je relatívna a absolútna drsnosť?

sin a + sin β = 2 sin (a + β)/2 . cos (a - β)/2

Prostredníctvom tejto identity, výsledná vlna a_R Zostane:

a_R = [2A Sen KX] . cos Ωt

Umiestnenie uzlov a brucha

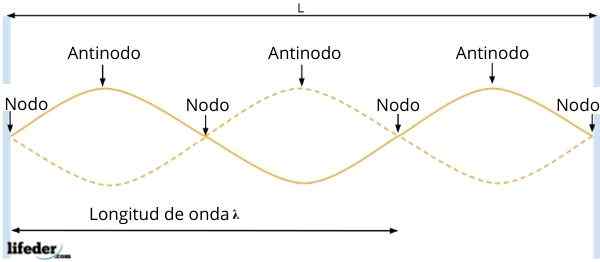Antinodos alebo brucho a uzly

Výsledná vlna má amplitúdu na_R = 2ase kx, ktorá závisí od polohy častice. Potom, v bodoch, pre ktoré sa Sen Kx = 0, amplitúda vlny zrušuje, to znamená, že neexistujú žiadne vibrácie.

Tieto body sú:

KX = π, 2π, 3π ..

Ako k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

V takýchto bodoch dochádza k deštruktívnemu zasahovaniu a nazývajú sa uzoly. Sú oddelené vzdialenosťou rovnajúcou sa λ/2, ako je odvodené od predchádzajúceho výsledku.

A medzi dvoma po sebe idúcimi uzlami sú Antinodos alebo brucho, v ktorej je amplitúda vlny maximálna, pretože dochádza k konštruktívnemu rušeniu. Vyskytujú sa, keď:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Opäť k = 2 π/ λ a potom:

x = λ /4, 3λ /4, 5λ /4, ..

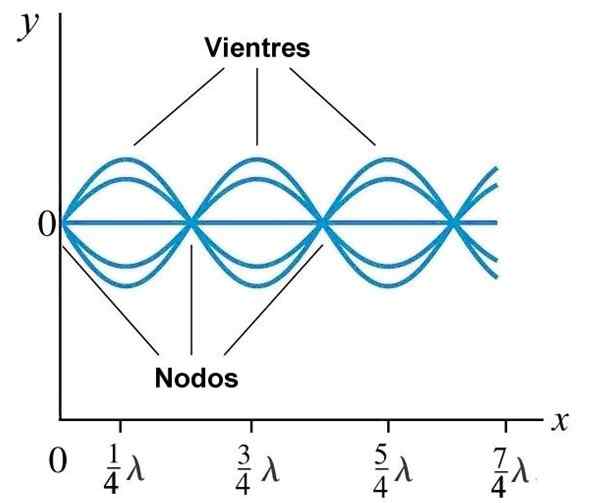Brucho alebo antinódy a uzly v stacionárnej vlne generovanej na lane s pevným koncom pri x = 0. Zdroj: Wikimedia Commons.

Normálne režimy na lane

Podmienky hraníc na lane určujú, ako sú vlnové dĺžky a frekvencie. Ak je lano s dĺžkou L fixované svojimi dvoma koncami, nemôže vibrovať s akoukoľvek frekvenciou, pretože body, v ktorých je lano fixované, sú už uzly.

Okrem toho je oddelenie medzi susednými uzlami λ/2 a medzi uzlom a bruchom je λ/4, týmto spôsobom sa vytvárajú iba pre určité vlnové dĺžky, ktoré sa vytvárajú stacionárne vlny: tie, v ktorých je upravené celé číslo n λ/2 vo vnútri. :

(λ/2) = l, s n = 1, 2, 3, 4 .. .

Preto:

λ = 2l/n

Harmonické

Rôzne hodnoty odobraté λ sa nazývajú harmonika. Máme teda:

-Prvá harmonická: λ = 2l

-Druhá harmonická: λ = l

-Tretia harmonická: λ = 2 l/3

-Harmonická miestnosť: λ = l/2

A tak ďalej.

Rýchlosť

Aj keď sa zdá, že stacionárna vlna sa nepohybuje, rovnica je stále platná:

v = λ. F

Preto:

v = (2l/n) . F

F = nv/2l

Teraz je možné preukázať, že rýchlosť, s akou sa vlna pohybuje v lane, závisí od napätia T v rovnakom a jeho lineárnej hustote hmoty μ (hmotnosť na jednotku dĺžky) ako:

Preto:

Môže vám slúžiť: mŕtve zaťaženie: Charakteristiky, výpočet, príklady

Vlastnosti stacionárnych vĺn

-Keď sú vlny stojace, výsledná vlna sa nerozširuje ako jej komponenty, ktoré siahajú z jedného miesta na druhé. Existujú body, kde y = 0, pretože neexistujú žiadne vibrácie: uzly, inými slovami, amplitúda na_R Je nula.

-Matematické vyjadrenie stacionárnej vlny pozostáva z produktu priestorovej časti (ktorá závisí od súradnice X alebo súradnice vesmíru) a časovej časti.

-Medzi uzlami výsledná čierna vlna osciluje na jednom mieste, zatiaľ čo vlny, ktoré idú z jedného miesta na druhé, sú zastarané.

-Práve v uzloch sa energia neprepravuje, pretože je to úmerné štvorcovi amplitúdy, ale je uväznená medzi uzlami.

-Vzdialenosť medzi susednými uzlami je polovica vlnovej dĺžky.

-Body, v ktorých je lano fixované, sa tiež považujú za uzly.

Chlapci

Stacionárne vlny v dimenzii

Vlny v pevnom lane sú príkladmi stacionárnych vĺn v dimenzii, ktorej matematický popis, ktorý sme ponúkli v predchádzajúcich oddieloch.

Stacionárne vlny v dvoch a troch rozmeroch

Stacionárne vlny môžu byť prezentované aj v dvoch a troch rozmeroch, čo je o niečo zložitejší matematický popis.

Pretekárske príklady ONDAS

Pevné reťazce

-Reťazec fixovaný extrémom, ktorý je kmitál ručne alebo s jedným piestom druhým generuje stacionárne vlny pozdĺž svojej dĺžky.

Hudobné nástroje

Stacionárne vlny sa vytvárajú v hudobných nástrojoch, ako je Violoncello. Zdroj: Pixabay.

-Pri hraní strunových nástrojov ako gitara, harfy, husle a klavír.

Vlny Stlover sa tiež vytvárajú vo vzduchových skúmavkách, ako sú orgánové trubice.

Budovy a mosty

Stacionárne vlny vznikajú v štruktúrach, ako sú mosty a budovy. Pozoruhodným prípadom bol prípad Tacoma Narrows Bridge v blízkosti mesta Seattle v Spojených štátoch amerických. Krátko po otvorení v roku 1940 sa tento most zrútil kvôli stacionárnym vlnám vytvoreným vo vetre.

Frekvencia vetra sa zhoduje s prirodzenou frekvenciou mosta, ktorá v tomto vytvára. Tento jav je známy ako rezonancia.

Môže vám slúžiť: svetlo odraz

Seiches

V prístavoch je veľmi zvedavý fenomén nazývaný Zavesiť, v ktorých vlny mora produkujú veľké oscilácie. Dôvodom je, že vody v prístave sú dosť uzavreté, hoci oceánske vody prenikajú tak často prostredníctvom vchodu do prístavu.

Port Waters sa pohybujú s vlastnou frekvenciou, ako aj s vodami oceánu. Ak sa obe vody zhodujú s ich frekvenciami, existuje veľká stacionárna vlna v dôsledku rezonancie, ako sa to stalo s mostom Tacoma.

Ten Seiches Môžu sa tiež vyskytnúť v jazerách, nádržiach, bazénoch a ďalších vodných vodách obmedzených povrchmi.

Rybie tanky

Stacionárne vlny môžu byť vytvorené v akváriu prepravovanej osobou, ak je frekvencia, s akou sa osoba rovná frekvencii výkyvu vody.

Cvičenie

Gitarové lano má l = 0.9 ma lineárna hustota cesta μ = 0.005 kg/m. Je vystavený 72 N napätia a jeho režim vibrácií je ten, ktorý zobrazuje obrázok, s amplitúdou 2A = 0.5 cm.

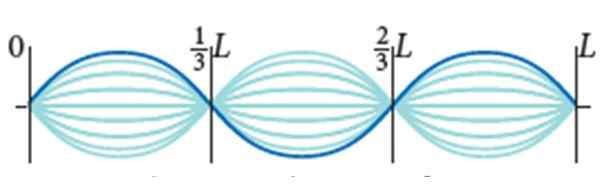Stacionárne vlny na gitarovom lane. Zdroj: Bauer, W. Fyzický.

Nájsť:

a) Rýchlosť šírenia

b) Frekvencia vlny

c) zodpovedajúca stacionárna vlnová rovnica.

Roztok

Cez:

Je získané;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Riešenie B

Vzdialenosť medzi dvoma susednými uzlami je λ/2, preto:

(2/3) L - (1/3) L = λ/2

(1/3) L = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Ako v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Riešenie c

Rovnica je:

a_R = [2A Sen KX] . cos Ωt

Musíme nahradiť hodnoty:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = Ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

Amplitúda 2A už je uvedená vo vyhlásení:

2A = 0.5 cm = 5 x 10 ^-3 m.

Preto:

a_R = 5 x 10 ^-3 m . Sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . Sin [(10π/3) x] . cos (400πt)

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 7. Vlny a kvantová fyzika. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil.
6. Wikipedia. Zavesiť. Obnovené z: je.Wikipedia.orgán.