Transcendentné čísla, ktoré sú, vzorce, príklady, cvičenia

Ten transcendentné čísla Sú to tie, ktoré nemožno získať v dôsledku polynomiálnej rovnice. Opak transcendentného čísla je a algebraické číslo, ktoré sú riešeniami polynómovej rovnice typu:

do_n Xⁿ + do_N-1 X^N-1 +… + A₂ X² + do₁ x + a₀ = 0

Kde koeficienty_n, do_N-1,..₂, do₁, do₀ Sú to racionálne čísla, nazývané polynómové koeficienty. Ak je číslo X riešením predchádzajúcej rovnice, potom toto číslo nie je transcendentné.

postava 1. Dva počty veľkých významov vo vede sú transcendentné čísla. Zdroj: verejné domény.slepo.

Budeme analyzovať niekoľko čísel a uvidíme, či sú alebo nie sú transcendentné:

a) 3 nie je transcendentné, pretože ide o roztok x - 3 = 0.

b) -2 nemôže byť transcendentný, pretože ide o riešenie x + 2 = 0.

c) ⅓ Je to 3x - 1 = 0 riešenie

d) riešenie rovnice x² - 2x + 1 = 0 je √2 -1, takže uvedené číslo podľa definície nie je transcendentné.

e) Ani √2, pretože je to výsledok rovnice x² - 2 = 0. Zvýšením √2 štvorca má za následok 2, ktoré odpočítali od 2, nezáleží na nule. Takže √2 je iracionálne číslo, ale nie je transcendentné.

[TOC]

Aké sú transcendentné čísla?

Problém je v tom, že neexistuje všeobecné pravidlo, ktoré by ste ich získali (neskôr povieme formu), ale niektoré z najslávnejších sú čísla pI a Neper, označené: respektíve: π a a.

Číslo π

Číslo π Prirodzene sa zdá, že pozoruje, že matematický kvocient medzi obvodom P kruhu a jeho priemerom D, bez ohľadu na to, či ide o malý alebo veľký kruh, vždy dáva rovnaké číslo, nazývané pI:

π = P/D ≈ 3 14159…

To znamená, že ak sa priemer obvodu považuje za jednotku merania, pre všetky z nich, či už veľké alebo malé, obvod bude vždy hodnotiť p = 3,14… = π, Ako je vidieť v animácii na obrázku 2.

Môže vám slúžiť: Bolzano veta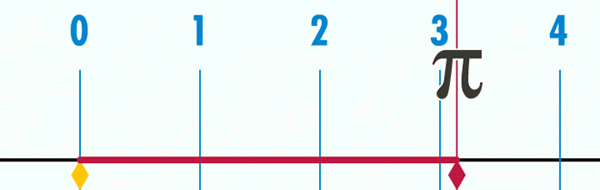Obrázok 2. Dĺžka obvodu kruhu je niekedy dĺžka priemeru, ktorá je približne 3,1416.

Aby ste určili viac desatinných miest, musíte zmerať viac presnosti P a D a potom vypočítať kvocient, ktorý sa uskutočnil matematickým spôsobom. Záver je, že desatinné miesta kvocientu nemajú koniec a nikdy sa neopakujú, takže číslo π Okrem toho, že je transcendentný, je tiež iracionálny.

Iracionálne číslo je toto číslo, ktoré nemožno vyjadriť ako rozdelenie dvoch celých čísel. 

Je známe, že každé transcendentné číslo je iracionálne, ale nie je pravda, že všetky iracionálne sú transcendentné. Napríklad √2 je iracionálny, ale nie je transcendentný.

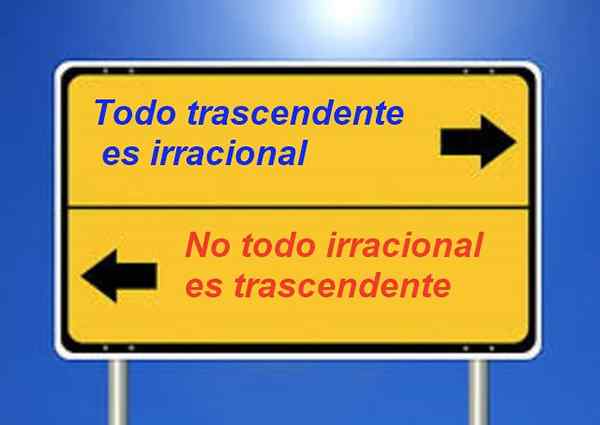Obrázok 3. Transcendentné čísla sú iracionálne, ale recipročné vyhlásenie nie je pravdivé.

Číslo e

Transcendentné číslo je základom Neperiánskych logaritmov a ich desatinný prístup je:

e ≈ 2.718281828459045235360… .

Ak ste chceli napísať číslo a Presne by bolo potrebné písať desatinné nekonečné, pretože každé transcendentné číslo je iracionálne, ako už bolo povedané.

Prvých desať číslic a Dajú sa ľahko zapamätať:

2.7 1828 1828 A hoci sa zdá, že sleduje opakujúci.

Formálnejšia definícia a je ďalší:

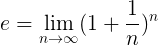
Čo znamená, že presná hodnota a Operácia uvedená v tomto vzorci sa dosiahne, keď je prirodzené číslo n Má tendenciu nekonečno.

To vysvetľuje, prečo môžeme získať iba prístupy a, Pretože akokoľvek veľké je číslo n, vždy nájdete a n starší.

Pozrime sa na nejaké prístupy sami:

-Keď n = 100 potom (1 + 1/100)¹⁰⁰ = 2 70481, ktoré sa sotva zhoduje v prvom desatinnom mieste s „skutočnou“ hodnotou E.

-Ak ste vybraní n = 10.000 máte (1 + 1/10.000)^10.000 = 2 71815, ktorá sa zhoduje s „presnou“ hodnotou E v prvých troch desatinných miestach.

Môže vám slúžiť: homológne strany

Tento proces by sa mal dodržiavať, aby bol schopný získať „skutočnú“ hodnotu E. Nemyslím si, že máme čas na to, ale urobme ešte jeden pokus:

Použime n = 100.000:

(1 + 1/100.000)^100.000 = 2,7182682372

Že má iba štyri desatinné miesta, ktoré sa zhodujú s hodnotou považovanou za presnú.

Dôležité je pochopiť, že čím väčšia je hodnota n vybranej na výpočet a_n, bližšie bude mať skutočnú hodnotu. Ale táto skutočná hodnota sa bude konať iba vtedy, keď n je nekonečná.

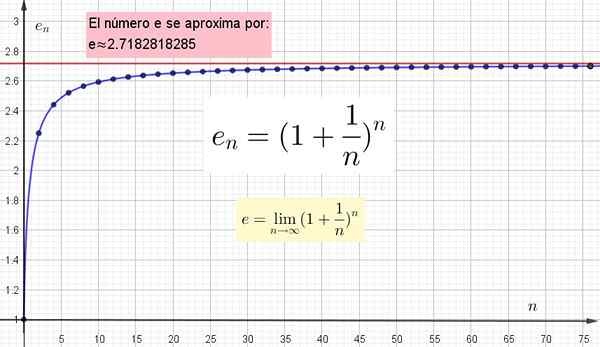Obrázok 4. Je graficky znázornená, pretože vyššia hodnota n je bližšie k E, ale aby dosiahla presnú hodnotu n.

Ostatné transcendentné čísla

Okrem týchto slávnych čísel existujú aj ďalšie transcendentné čísla, napríklad:

- 2^√2

Akékoľvek algebraické číslo, ktoré nie je 0 alebo 1, zvýšené na iracionálny exponent bude transcendentné číslo.

-Číslo 10 ChamperNowne: 

C_10 = 0,123456789101112131415161718192021… .

-Číslo ChamperNowne na základni 2:

C_2 = 0,110111001011011… .

-Y alebo konštantné gama číslo Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

To sa získa vykonaním nasledujúceho výpočtu:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Kedy n byť veľmi veľký. Ak chcete mať presnú hodnotu čísla gama, bolo by potrebné vypočítať pomocou n nekonečný. Niečo podobné tomu, čo sme urobili vyššie.

A existuje oveľa viac transcendentných čísel. Veľký matematik Georg Cantor, narodený v Rusku a žil v rokoch 1845 až 1918, ukázal, že sada transcendentných čísel je oveľa väčšia ako sada algebraických čísel.

Vzorce, kde sa objaví transcendentné číslo π

Obvod obvodu

P = π d = 2 π r, kde p je obvod, d priemer a r polomer obvodu. Je potrebné si uvedomiť, že:

Môže vám slúžiť: Koľko musíte pridať do 3/4, aby ste dostali 6/7?

-Priemer obvodu je najdlhší segment, ktorý sa pripojí k jeho dvom bodom a ktorý vždy prechádza jeho stredom,

-Polomer je polovica priemeru a je segment, ktorý prechádza zo stredu k okraju.

Kruhová plocha

A = π r² = ¼ π d²

Povrch

S = 4 π r^2.

Jo. Aj keď sa to nezdá, povrch gule je rovnaký ako povrch štyroch kruhov rovnakého polomeru ako guľa.

Objem

V = 4/3 π r³

Cvičenia

- Cvičenie 1

„Exotická“ pizzeria predáva pizzu s tromi priemermi: 30 cm, stredná 37 cm a veľká 45 cm. Dieťa je veľmi hladné a uvedomilo si, že dve malé pizze majú rovnaké náklady ako veľké. Čo bude pre neho lepšie, kúpte si dve malé pizze alebo veľké?

Obrázok 5.- Oblasť pizze je úmerná štvorcovi polomeru, čo je konštantná proporcionalita. Zdroj: Pixabay.

Riešenie

Čím väčšia je oblasť, tým väčšia je množstvo pizze, z tohto dôvodu sa bude vypočítať oblasť veľkej pizze a porovnaná s množstvom dvoch malých pizze:

Veľká pizza = ¼ π d² = ¼ ⋅3,14162545² = 1590,44 cm²

Malá pizza = ¼ π d² = ¼ ⋅3 14162030² = 706,86 cm²

Preto budú mať dve malé pizzy 

2 x 706,86 = 1413,72 cm² .

Je to jasné: bude kupovať viac pizze jedného veľkého ako dvaja najmenší.

- Cvičenie 2

„Exotická“ pizzeria tiež predáva 30 cm polomer polomer -man -Pizza pre rovnaký obdĺžnikový tvar 30 x 40 cm strany. Ktoré by ste si vybrali?

Obrázok 6.- Povrch semi -špice je dvojnásobný kruhový povrch základne. Zdroj: f. Zapata.

Riešenie

Ako je uvedené v predchádzajúcej časti, povrch gule je štyrikrát väčší ako povrch kruhu s rovnakým priemerom, takže semifinále s priemerom 30 cm bude mať:

30 cm semi -man -man -Pizza: 1413,72 cm² (dvakrát kruh s rovnakým priemerom)

Obdĺžniková pizza: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -Pizza má väčšiu oblasť.

Odkazy

1. Fernández J. Číslo e. Pôvod a kuriozity. Obnovené z: sójovej matematiky.com
2. Užite si matematiku. Eulerove číslo. Získané z: Vychutnajte si.com.
3. Figuera, J. 2000. Matematika 1. Diverzifikovaný. Edície Co-Bo.
4. Garcia, m. Číslo E v elementárnom výpočte. Obnovené z: matematiky.Cins.UCV.ísť.
5. Wikipedia. PI Číslo. Získané z: Wikipedia.com
6. Wikipedia. Transcendentné čísla. Získané z: Wikipedia.com