Perfektné čísla, ako ich identifikovať a príklady

A Perfektné číslo je prirodzené číslo také Súčet jeho deliacich je rovnaký ako číslo. Je zrejmé, že to nemôže byť zahrnuté medzi deliteľmi do samotného čísla.

Jedným z najjednoduchších príkladov dokonalého čísla je 6, pretože jeho deliteľstvo sú: 1, 2 a 3. Ak pridáme deližory, získa sa: 1 + 2 + 3 = 6.

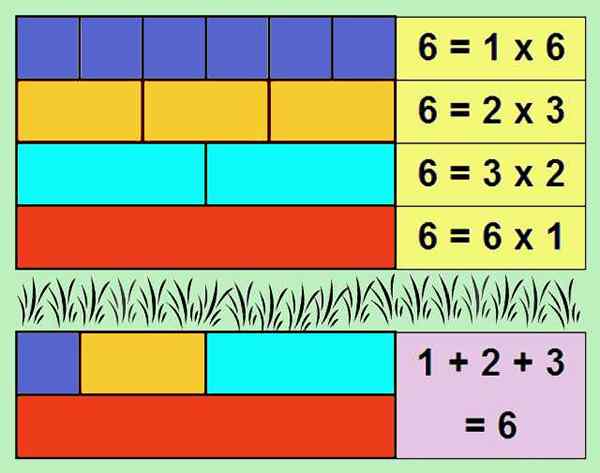postava 1. Číslo 6 je perfektné, pretože súčet svojich deliteľov, okrem samotného čísla, dáva číslo 6. Zdroj: Self Made

Súčet deliteľov celého čísla, okrem samotného čísla, sa nazýva alikvot. Preto sa perfektné číslo rovná jeho alikvotu.

Ale ak je v súčtu deliacich čísel, číslo samotné je zahrnuté, potom bude dokonalým číslom, v ktorom sa súčet všetkých jeho deliacich vydelí 2, ktorý sa rovná samotnému číslu.

[TOC]

História

Matematici staroveku, najmä Gréci, dali dokonalé čísla veľký význam a pripisovali božské vlastnosti.

Napríklad, Philo de Alejandría, okolo 1. storočia, tvrdil, že 6 a 28 sú dokonalé čísla, ktoré sa zhodujú so šiestimi dňami stvorenia sveta a dvadsiatimi ôsmimi dňami, ktoré potrebujú, kým sa mesiac otočí okolo Zeme.

Perfektné čísla sú tiež prítomné v prírode, napríklad v severnom póle Saturn sa tiež javí ako perfektné číslo 6, šesťuholníkový vír, ktorý zistil sonda Cassini a ktorá zaujala vedcom. 

Včely majú bunky v šesťuholníkovej forme, to znamená so 6 stranami.  Je ukázané, že polygón s dokonalým číslom 6 je ten, ktorý umožňuje maximalizáciu počtu buniek v úli včely, s minimálnym voskom pre jeho vypracovanie.

Obrázok 2. Perfektné číslo 6 je prítomné v včelách. Je ukázané, že s týmto počtom strán je množstvo vosku, ktoré sa má použiť na vytvorenie buniek, minimálne. Zdroj: Pixabay.

Perfektné čísla Vlastnosti

Súčet všetkých deliteľov prírodného čísla n je označený σ (n). V perfektnom čísle je pravda, že: σ (n) = 2n.

Euklid vzorec a kritériá

Euclid objavil vzorec a kritérium, ktoré vám umožní nájsť perfektné čísla. Tento vzorec je:

2^(N-1) (2ⁿ -1)

Číslo generované vzorcom bude však perfektné iba vtedy, keď je faktor (2ⁿ -1) Buďte bratranec.

Môže vám slúžiť: obdĺžnikové komponenty vektora (s cvičeniami)

Pozrime sa, ako sa generujú prvé dokonalé čísla:

Ak n = 2, potom máme 2¹ (2² - 1) = 2 x 3 = 6, ktoré sme už videli, že je perfektný.

Keď n = 3 máš 2² (2³ - 1) = 4 x 7 = 28, čo je tiež perfektné, pretože sa podrobne overuje v príklade 1.

Pozrime sa, čo sa stane s n = 4. Nahradením vo vzorci euklid, ktorý máme:

2³ (2⁴ - 1) = 8 x 15 = 120

Je možné overiť, že toto číslo nie je dokonalé, ako je uvedené podrobne v príklade 3. To nie je v rozpore s euklidovými kritériami, pretože 15 nie je bratranec, čo je nevyhnutná požiadavka na to, aby bol výsledok dokonalým číslom.

Pozrime sa, čo sa stane, keď n = 5. Uplatňovanie vzorca, ktorý máme:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Ako 31 je hlavné číslo, takže číslo 496 musí byť podľa euclidových kritérií dokonalé. V príklade 4 je podrobne znázornené, že je to efektívne.

Čísla prvočísla, ktoré majú formulár 2^p - 1 sa nazývajú bratranci Mersenne, na počesť mnícha Marina Mersenna, ktorý študoval hlavné čísla a perfektné čísla späť v sedemnástom storočí.

Následne v osemnástom storočí Leonhard Euler ukázal, že všetky perfektné číslo generované euklidovým vzorcom sú páry.

K dnešnému dňu sa zistilo, že je perfektný, ktorý je nepárny.

Najväčšie dokonalé známe číslo

K aktuálnemu dátumu je známych 51 dokonalých čísel, všetky generované kritériami vzorca a euklidov. Toto číslo sa získalo, keď sa našla Mersenneho bratranec, čo je: (2^82589933 - 1).

Perfektné číslo #51 je (2^82589933) X (2^82589933 - 1) a má 49724095 Digitos.

Perfektné číslo je priateľom

V teórii čísel sa hovorí, že dve čísla sú priatelia, keď sa súčet deliteľov jedného, ​​okrem samotného čísla, sa rovná druhému číslu a naopak.

Môže vám slúžiť: linka a segment semiférií

Čitateľ môže overiť, či súčet deliacich 220, okrem 220, je 284. Na druhej strane, súčet deliacich 284, okrem 284, sa rovná 220. Preto čísla pár 220 a 284 sú priatelia.

Z tohto hľadiska je perfektné číslo priateľom.

Príklady dokonalých čísel

Ďalej je uvedených prvých osem dokonalých čísel:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Cvičenia

V nasledujúcich cvičeniach bude potrebné vypočítať deliteľov čísla a potom ich urobiť a overiť, či je číslo perfektné číslo alebo nie.

Preto pred riešením cvičení preskúmame koncept a ukážeme, ako sa vypočítame.

Ak chcete začať, musíte si uvedomiť, že čísla môžu byť bratrancami (keď sa dajú rozdeliť iba na presnú so sebou a 1) alebo zlúčeniny (keď sa môžu rozložiť ako produkt prvých čísel).

Pre zložené číslo n: Máte:

N = aⁿ . b^m. c^p ... r^{klimatizovať} 

Kde a, b, c ... r sú prvotné čísla a n, m, p ... k sú exponenti patriaci k prírodným číslom, ktoré môžu mať hodnotu od 1 ďalej.

Pokiaľ ide o týchto exponentov, existuje vzorec, aby ste vedeli, koľko deliteľov má číslo n, hoci nám to nehovorí, čo to je. Nech C je táto suma, potom:

C = (n +1) (m +1) (p +1) ... (k +1)

Rozklad čísla n ako produktu hlavných čísel a znalosť toho, koľko deliteľov má, bratranci, ako aj non -cousins, nám pomôže určiť, čo sú títo deliaci.

Akonáhle má každý, s výnimkou posledného, ​​ktorý sa v sume nevyžaduje, dá sa overiť, či je to perfektné číslo alebo nie.

- Cvičenie 1

Overte, či je číslo 28 perfektné.

Riešenie

Prvým bude rozložiť číslo vo svojich hlavných faktoroch.

28 | 2
14 | 2
07 | 7
01 | 1

Jeho deliteľmi sú: 1, 2, 4, 7, 14 a 28. Ak vylúčime 28, súčet Divisors dáva:

Môže vám slúžiť: polovica z 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Preto je 28 perfektné číslo.

Okrem toho súčet všetkých svojich deliteľov je 28 + 28, takže pravidlo σ (28) = 2 x 28.

- Cvičenie 2

Rozhodnite sa, či je číslo 38 perfektné alebo nie.

Riešenie

Toto číslo je rozdelené do svojich hlavných faktorov:

39 | 3
13 | 13
01 | 1

Deliéri 39 bez zahrnutia samotného čísla sú: 1, 3 a 13. Súčet 1 + 3 + 13 = 4 + 13 = 17 sa nerovná 39, preto 39 je nedokonalé alebo nekonečné číslo. 

- Cvičenie 3

Zistite, či je číslo 120 dokonalé alebo nedokonalé.

Riešenie

Toto číslo je rozdelené do svojich hlavných faktorov:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Z hlavných faktorov sa nachádzajú delení:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 a 120

Ak bolo 120 perfektných, keď by sa malo pridať všetky jeho deliteľy 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Tento výsledok sa jasne líši od 240, takže sa dospelo k záveru, že číslo 120 nie je dokonalé číslo.

- Cvičenie 4

Overte, či je číslo 496, získané podľa kritérií euklidov, perfektné číslo.

Riešenie

Číslo 496 je rozdelené do svojich hlavných faktorov:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Potom sú ich deliaci::

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Teraz sú všetky pridané, s výnimkou 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Potvrdzujúc, že ​​je to skutočne perfektné číslo.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Všetko o prvých číslach. Priatelia čísla. Uzdravený z: sestry.orgán.
3. Wolfram Mathworld. Eulerov pravidlo. Obnovené z: Mathworld.Valfram.com.
4. Wolfram Mathworld. Perfektné číslo. Obnovené z: Mathworld.Valfram.com.
5. Wikipedia. Perfektné čísla. Zdroj: In.Wikipedia.orgán.
6. Wikipedia. Priatelia čísla. Obnovené z: je.Wikipedia.orgán.