História iracionálnych čísel, vlastnosti, klasifikácia, príklady

Ten iracionálne čísla Sú to tí, ktorých desatinná expresia má nekonečné postavy bez opakujúceho sa vzoru, a preto ich nemožno získať vytvorením kvocientu medzi akýmikoľvek dvoma celkovými číslami.

Medzi najznámejšie iracionálne čísla patrí:

postava 1. Z zhora nadol nasledujúce iracionálne čísla: PI, počet Eulerov, Aúrea a dva druhé druhy druhej štvorca. Zdroj: Pixabay.

Medzi nimi je bezpochyby π (pi) najznámejší, ale je ich oveľa viac. Všetci patria do súboru reálnych čísel, čo je numerická súprava, ktorá spája racionálne a iracionálne čísla.

Podporné body na obrázku 1 naznačujú, že desatinné miesta nasledujú neurčito, čo sa stane, že priestor súčasných kalkulačiek umožňuje iba zobraziť niekoľko.

Ak sa pozrieme pozorne, za predpokladu, že vytvoríme kvocient medzi dvoma celkovými číslami, získa sa desatinné miesto s obmedzenými číslami alebo ak nie, s nekonečnými číslami, v ktorých sa jeden alebo viac opakuje. To sa nestane s iracionálnymi číslami.

[TOC]

História iracionálnych čísel

Veľký matematik staroveku Pythagoras, narodený v roku 582.C v Samos, Grécko, založil Pythagorovu školu myslenia a objavil slávnu vetu, ktorá nesie jeho meno. Máme to doľava (Babylončania ho už mohli poznať dlho predtým).

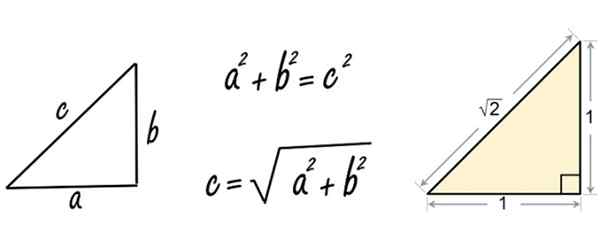Obrázok 2. Pythagorská veta aplikovaná na trojuholník strany rovnajúcich sa 1. Zdroj: Pixabay/Wikimedia Commons.

Keď Pythagoras (alebo pravdepodobne jeho učeník) aplikoval vetu na pravý trojuholník strany rovnajúcich sa 1, zistil iracionálne číslo √2.

Môže vám slúžiť: sušenie čiary

Urobil to takto:

C = √1² + 1² = √1+1 = √2

A okamžite si uvedomil, že toto nové číslo nepochádzalo z kvocientu medzi dvoma ďalšími prírodnými číslami, ktoré boli známe v tom čase.

Preto ho zavolal iracionálny, A objav spôsobil veľkú úzkosť a zmätok medzi Pythagorejanmi.

Vlastnosti iracionálnych čísel

-Sada všetkých iracionálnych čísel je označená písmenom I a niekedy ako Q* alebo Q^C. Únia medzi iracionálnymi číslami I alebo Q* a racionálnymi číslami Q, vedie k súboru skutočných čísel N.

-Pri iracionálnych číslach je možné vykonať známe aritmetické operácie: súčet, odčítanie, násobenie, delenie, potenciácia a ďalšie.

-Rozdelenie medzi 0 nie je definované medzi iracionálnymi číslami.

-Súčet a produkt medzi iracionálnymi číslami nie sú nevyhnutne ďalším iracionálnym číslom. Napríklad:

√2 x √8 = √16 = 4

A 4 nie je iracionálne číslo.

-Súčet racionálneho čísla plus iracionálne vedie k iracionálnemu. Tadiaľto:

1 + √2 = 2.41421356237…

-Produkt iného racionálneho čísla od 0 podľa iracionálneho čísla je tiež iracionálny. Pozrime sa na tento príklad:

2 x √2 = 2.828427125…

-Inverzia iracionálneho výsledku k ďalšiemu iracionálnemu číslu. Skúsme nejaké:

1 / √2 = 0.707106781…

1 / √3 = 0.577350269…

Tieto čísla sú zaujímavé, pretože sú tiež hodnotami niektorých trigonometrických dôvodov známych uhlov. Veľa z trigonometrických dôvodov sú iracionálne čísla, ale existujú výnimky, ako napríklad Sen 30 ° = 0.5 = ½, čo je racionálne.

-V tejto sume sú splnené komutatívne a asociatívne vlastnosti. Ak sú A a B dve iracionálne čísla, znamená to, že:

Môže vám slúžiť: Prepríjemná funkcia: Definícia, vlastnosti, príklady

A + b = b + a.

A ak je C ďalšie iracionálne číslo, potom:

(A + b) + c = a + (b + c).

-Distribučná vlastnosť násobenia vzhľadom na sumu je ďalšou známym vlastníctvom, ktoré je tiež splnené pre iracionálne čísla. V tomto prípade:

do.(b+c) = a.B + a.c.

-Iracionálne pre svoj opak: -a. Po pridaní výsledku je 0:

A+(-a) = 0

-Medzi dvoma rôznymi racionálnymi sú najmenej jedno iracionálne číslo.

Umiestnenie iracionálneho čísla na skutočnom riadku

Skutočná čiara je horizontálna čiara, v ktorej sa nachádzajú reálne čísla, z ktorých iracionálne sú dôležitou súčasťou.

Aby sme našli iracionálne číslo na reálnom riadku, v geometrickej podobe, môžeme stáť za to, že Pythagoras bude, pravidlo a kompas.

Ako príklad sa chystáme nájsť √5 na skutočnej čiare, pre ktorú nakreslíme obdĺžnikový trojuholník bokov x = 2 a y = 1, Ako ukazuje obrázok:

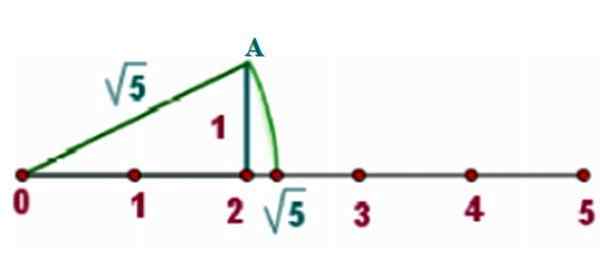Obrázok 3. Metóda lokalizácie iracionálneho čísla na reálnom riadku. Zdroj: f. Zapata.

Pre vetu Pythagorov je hypotenusom takého trojuholníka:

C = √2² + 1² = √4+1 = √5

Teraz je rytmus hrotom umiestnený na 0, kde je tiež jeden z vrcholov pravého trojuholníka. Špička ceruzky kompasu musí byť vo vrchole.

Nakresli sa obvod obvodu, ktorý znižuje skutočnú čiaru. Pretože vzdialenosť medzi stredom obvodu a akýmkoľvek bodom je polomer, ktorý má hodnotu √5, bod križovatky je tiež √5 od stredu.

Grafu je zrejmé, že √5 je medzi 2 a 2.5. Kalkulačka nám ponúka približnú hodnotu:

Môže vám slúžiť: určovací koeficient: vzorce, výpočet, interpretácia, príklady

√5 = 2.236068

A tak, budovanie trojuholníka s príslušnými stranami, ostatné iracionálne sa môžu nachádzať, napríklad √7 a ďalšie.

Klasifikácia iracionálnych čísel

Iračné čísla sú rozdelené do dvoch skupín:

-Algebraický

-Transcendentálny

Algebraické čísla

Algebraické čísla, ktoré môžu byť iracionálne alebo nie, sú riešenia polynómových rovníc, ktorých všeobecná forma je:

do_n Xⁿ + do_N-1X^N-1 + do_N-2X^N-2 +.. . +do₁x + a_ani = 0

Príkladom polynómovej rovnice je rovnica druhého stupňa, ako je táto:

X³ - 2x = 0

Je ľahké preukázať, že iracionálne číslo √2 je jedným z riešení tejto rovnice.

Transcendentné čísla

Namiesto toho, transcendentné čísla, aj keď iracionálne, nikdy nevznikajú ako riešenie polynómovej rovnice.

Transcendentné čísla, ktoré sa nachádzajú najčastejšie v aplikovanej matematike, sú π, pre ich vzťah s obvodom a číslom E alebo Eulera, ktorý je základom Neperiánskych logaritmov.

Cvičenie

Na čiernom štvorci sa v polohe uvedenej na obrázku umiestni sivá. Je známe, že povrch čierneho štvorca je 64 cm². Koľko sú dĺžky oboch štvorcov?

Obrázok 4. Dva štvorky, z ktorých sa nachádza dĺžka bokov. Zdroj: f. Zapata.

Odpoveď

Povrch štvorca strany L je:

A = l²

Pretože čierny štvorec je 64 cm² oblasti, jej strana musí byť 8 cm.

Toto opatrenie je rovnaké ako Diagonálny šedého štvorca. Aplikujte vetu Pythagory na túto diagonálu a pamätáte si, že strany štvorca merajú rovnako, budeme mať:

8² = L_g² + L_g²

Kde l_g Je to strana šedého štvorca.

Preto: 2L_g² = 8²

Aplikácia druhej odmocniny na oboch stranách rovnosti:

L_g = (8/√2) cm

Odkazy

1. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
2. Figuera, J. 2000. Matematika 9. Stupeň. Edície Co-Bo.
3. Jiménez, r. 2008. Algebra. Sála.
4. Vzdelávací portál. Iracionálne čísla a ich vlastnosti. Zdroj: Portaledactive.slepo.
5. Wikipedia. Iracionálne čísla. Obnovené z: je.Wikipedia.orgán.