Nepárne čísla

Čo sú nepárne čísla?

Ten nepárne čísla Sú to celé čísla, ktoré nie sú deliteľné 2. To znamená, že s nepárnymi množstvami nemôžete robiť skupiny 2, napríklad ak má niekto 9 cukroviniek, ktoré by sa mohol podeliť s priateľom a nechce sa deliť, dotknú sa 4 cukrovinky a ďalších 5.

Niektoré z nepárnych čísel sú nasledujúce: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  V tomto výraze sú podnetové body naznačené, že existuje viac čísel, vľavo aj vpravo.

Obrázok 1: Ako zistiť, či je číslo nepárne?

Pozorne vidíte, že každé nepárne číslo je možné získať pridaním 2 do predchádzajúceho čísla. Napríklad, ak pridáme 2 až -1, dostanete 1, ak urobíme 1 + 2, je to 3 atď.

Tiež sa pozoruje, že ak sú páry rozptýlené, vrátane 0, ktoré sa považuje za párne číslo, získa sa sada celých čísel Z.

To je dôvod, prečo je možné napísať akékoľvek nepárne prirodzené číslo vo forme 2n + 1, kde n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, kde symbol ± znamená, že sa dá považovať za pozitívny alebo ako negatívny.

V prípade väčšieho počtu sa dá rozpoznať, keď je nepárny, pretože vždy končí 1, 3, 5, 7 alebo 9. Napríklad 1571 je nepárne a rovnako ako negatívne celé číslo -152.489.

Príklady nepárnych čísel

Časté čísla sú často prezentované v prírode a medzi nimi má číslo 3 osobitný význam. Pozrime sa na niekoľko príkladov:

-Existuje veľa kvetov s nepárnym počtom okvetných lístkov.

-Máme na každej ruke 5 prstov.

Môže vám slúžiť: náhodná premenná: koncept, typy, príklady

-Ľudské bytosti majú 23 párov chromozómov.

-Existujú 3 zákony Newtonu a 3 zákony termodynamiky.

-Jadrá atómov, ktoré majú nepárny počet protónov a neutrónov.

-Magi sú 3.

-V príbehoch a príbehoch sa často objavuje číslo 3, napríklad romány ako ako Traja mušketieri Autor: Alejandro Dumas a v populárnych príbehoch, ako napríklad Traja bratia a Tri malé prasiatka.

-Pre umelecké zloženie je volanie Podivné pravidlo, čo ustanovuje, že kompozícia s nepárnym počtom prvkov je atraktívnejšia ako jedno s párom. Nepárne číslo dodáva dynamiku, zatiaľ čo jeden pár poskytuje stabilitu.

Obrázok 2. Podivný počet prvkov pridáva do obrazu dynamiku

-Bežná stratégia na to, aby ceny objektov vyzerali lacnejšie, je skončiť 9, napríklad 2.99 dolárov, 39 dolárov a tak ďalej.

-Číslo 13 sú niektorými považované za smolu, zatiaľ čo iní pripisujú mystické vlastnosti 11, obe nepárne čísla.

Primo

Primo čísla, tí, ktorí sa pripúšťajú iba ako samotní deliaci a 1, sú čudní, s výnimkou 2, čo je jediný krútiaci moment bratranca.

Je možné preukázať, že akékoľvek číslo sa môže rozdeliť ako produkt hlavných faktorov (vrátane týchto právomocí) a že tento spôsob vyjadrenia čísla je jedinečný, s výnimkou poradia faktorov.

Napríklad číslo 45 je možné rozdeliť ako 45 = 3³ x 5.

Operácie s nepárnymi číslami

S nepárnymi číslami sa vykonávajú všetky aritmetické operácie a niektoré majú vynikajúce vlastnosti.

Môže vám slúžiť: Symbolizácia výrazov

- Sumy a výrobky

-Súčet dvoch nepárnych čísel má za následok párne číslo: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Pridaním nepárneho čísla s jedným krútiacim momentom je výsledok nepárny: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Ak n prvé prírodné, nepárne a nasledujúce čísla, výsledok je n². Pozrime sa na to s trochu podrobnejšími detailmi:

Pre n = 2: 1 + 3 = 4 = 2²

Pre n = 3: 1 + 3 + 5 = 9 = 3²

Pre n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Ak sa nepárne vynásobí pár, párne číslo pochádza: 7 x 4 = 28; (-3) x 12 = -36.

-Vynásobenie dvoch nepárnych čísel je tiež získané nepárne: 3 x 5 = 15; (-5) x (+11) = -55.

- Právomoci

-Ak sa kladné číslo zvýši na nepárny výkon, je to kladné číslo, napríklad: 3³ = 27.

-Zvýšením záporného čísla na nepárny výkon je výsledok negatívny: (-2)³= (-2) x (-2) x (-2) = -8.

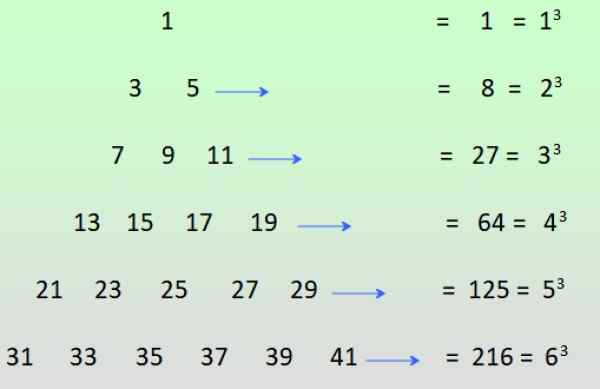
-Podivné sily pozitívnych celých čísel sa dajú dosiahnuť, ak sú k dispozícii nepárne čísla, ako je to znázornené na obrázku a pridané riadky:

Obrázok 3. Získanie nepárnych síl zo súčtu nepárnych čísel. Zdroj: f. Zapata.

Vyriešené cvičenia

- Cvičenie 1

Rozhodnite sa, či je výsledok nasledujúcej operácie párne alebo nepárny:

(53476890083 + 1987628967) x 13567903

Riešenie

Ak chcete získať odpoveď, nemusíte bežať, aby ste hľadali kalkulačku, ale na použitie videných vlastností. Pozrime sa na posledné číslice dodatkov, ktoré sú 3 a 7:

53476890083  + 1987628967

To znamená, že závislí sú čudní a už vieme, že súčet dvoch nepárnych čísel je rovný.

Obrázok, ktorý je výsledkom zátvorky, je teda rovnomerne a my sa vynásobíme číslom, ktoré končí na 3:

Môže vám slúžiť: Vektorová algebra

13567903

Čo znamená, že toto číslo je nepárne.

Vo vyššie uvedených vlastnostiach sa zistilo, že znásobenie krútiaceho momentu X je párne číslo. Preto je výsledná operácia rovnomerná.

- Cvičenie 2

Koľko stojí súčet prvých 5 po sebe idúcich nepárnych čísel? A to z prvých 50?

Riešenie

Súčet prvých 5 po sebe idúcich nepárnych čísel je:

1 + 3 + 5 + 7 + 9 = 25

Ale ak chceme pridať prvých 50 týmto spôsobom, je to ťažkopádne, takže ideme do vlastností. Potvrdzujú, že suma po sebe idúcich nepárnych čísel je n². V tomto prípade n = 50 a požadovaná suma je:

päťdesiat² = 50 x 50 = 2500.

- Cvičenie 3

Keď sa pridajú tri po sebe idúce nepárne čísla, získa sa 237. Aké sú čísla?

Riešenie

Zavolajme na naše prvé nepárne číslo a druhé a z do tretieho, podľa vyhlásenia, ktoré je splnené, že:

x + y + z = 237

V algebraickom jazyku je možné všetky nepárne číslo napísať vo formulári 2n +1. Urobme naše prvé nepárne číslo:

x = 2n +1

Pridajme 2, aby sme dostali nasledujúce nepárne:

y = x + 2 = (2n + 1) + 2 = 2n + 3

A nakoniec sa pridá znova 2, aby sa získal tretí nepárny:

Z = (2n +3) + 2 = 2n + 5

To všetko dodáva:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

To má za následok jednoduchú lineárnu rovnicu, ktorej riešenie je:

n = 38

A teraz s hodnotou n = 38 existujú tri objednávky:

x = (2 × 38) + 1 = 77

Preto sú zvláštne po sebe nasledujúce:

y = 79

Z = 81

A čitateľ môže ľahko overiť, či súčet týchto troch je 237.

Odkazy

1. Baldor, a. 1986. Aritmetika. Vydania a distribúcie Codex.
2. Štvrte, L. Nepárne čísla a právomoci prírodných čísel. Zdroj: Sinewton.orgán.
3. Brilantný. Rovnomerné a nepárne čísla. Zotavené z: brilantného.orgán.
4. Matematika 18. Operácie s nepárnymi číslami. Zdroj: Mathematics18.com.
5. Wikipedia. Rovnomerné a nepárne čísla. Obnovené z: je.Wikipedia.orgán.