Matematika

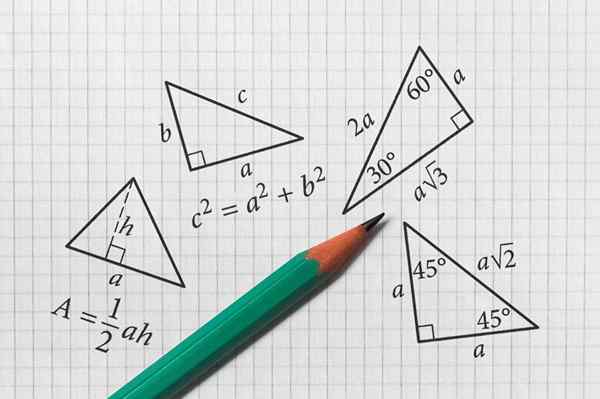
Uhly a trojuholníky

Uhly a trojuholníky
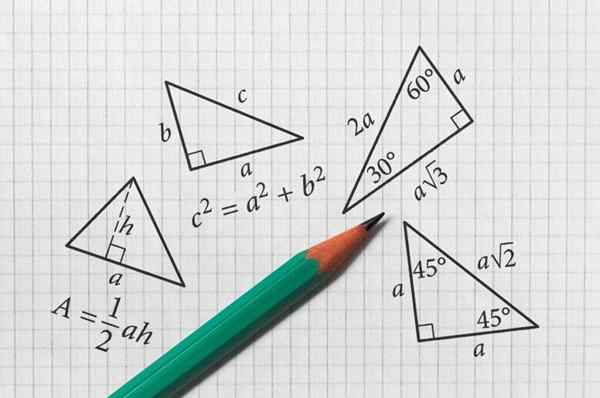Uhly a trojuholníky sú súčasťou plochej geometrie. Rúno

Čo sú uhly a trojuholníky?

A uhol Je to oblasť lietadla vymedzeného dvoma semifinále s spoločným bodom pôvodu. Tento bod je známy ako vrchol, Zatiaľ čo sa volá semifinále strany. Na druhej strane, a trojuholník Je to postava troch uhlov a troch strán, s tromi vrcholmi.

Najprv budeme hovoriť o uhloch.

Uhly

Existuje niekoľko spôsobov, ako označiť uhly: prostredníctvom gréckych písmen, ako je a, β, γ, ku ktorým je možné pridať prízvuk obvodu; s čalúnenými alebo malými písmenami, A, B, C, A, B, C; čísla, napríklad 1, 2, 3 ... alebo pomocou symbolu uhla ∠.

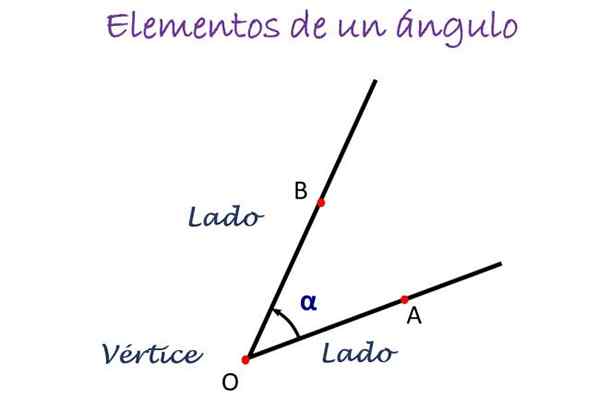Hlavné prvky uhla. Zdroj: f. Zapata

Na obrázku vyššie sa uhol meria od strany A do B, označený smerom šípky a v strede je písmeno, ktoré označuje vrchol, umiestnené, ktoré je normálne alebo. Uhol sa potom označuje ako ∠ AOB.

Keď sa uhol merať v zmysle antihorária, značka A +je ľubovoľne priradená a ak sa meria v harmonograme, značka -rozlíšiť ich.

Miera uhlov sa vykonáva pomocou transportéra, ktorý pozostáva z polkruhového plastového listu, ako je ten, ktorý je uvedený nižšie. Polkruh je rozdelený do 180 rovnakých častí, z ktorých každé volanie stupeň.

Na meranie, vrchol uhla sa zhoduje s centrálnym bodom transportéra, označený šípkou a počiatočnou stranou s jednou z okrajov, vnútorných alebo vonkajších. Posledná strana pretína niektoré značky prepravcu, toto opatrenie je uhol.

Môže vám slúžiť: Empirické pravidlo: Ako ho uplatniť, na čo je to vyriešené cvičenia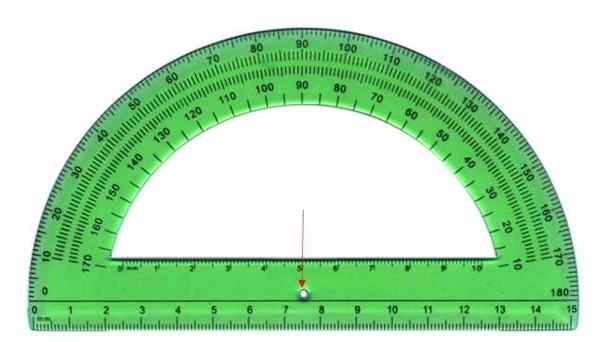Dopravník je nástroj na meranie uhlov. Zdroj: Wikimedia Commons

Typy uhlov

Jedným z najpoužívanejších kritérií na klasifikáciu uhlov je podľa jeho opatrenia. Preto môže byť uhol:

  • Nulový, opatrenia 0 °.
  • Ostrý, ktorého opatrenie je medzi 0 a 90 °.
  • Priamy, Meria presne 90 °.
  • Tupý, Je väčší ako 90 ° a menej ako 180 °.
  • Plochý, Jeho miera sa rovná 180 °.
  • Dokončiť, predstavuje úplný zákrut a meria 360 °.
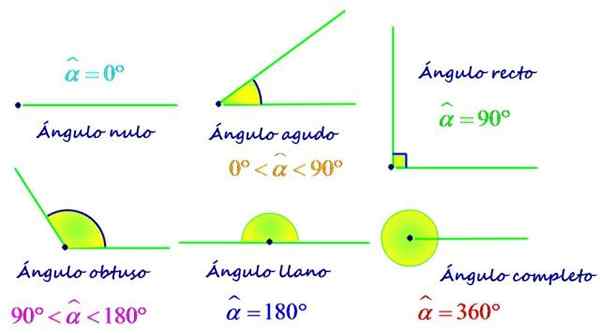Typy uhlov podľa vášho opatrenia. Zdroj: f. Zapata.

Podľa vzťahu medzi jeho mierou a vzťahom plochého uhla, ktorý je 180 °, môžu byť uhly tiež klasifikované ako:

  • Konkávny, Ak meria menej ako 180 °. Preto sú akútne, priame a tupé uhly konkávne, pretože jeho miera je vždy menšia ako 180 ° (pozri obrázok vyššie).
  • Vypuklý, Ak je vaše opatrenie väčšie ako 180 °, ako uhly 270 ° a 360 °.

Uhly podľa súčtu ich opatrení a podľa polohy ich strán

Dva uhly ∠ A a ∠ B môžu byť:

  • Doplnkový, Ak sa súčet jeho opatrení rovná 90 °.
  • Doplnkový, Pri pridávaní príslušných opatrení sa získa 180 °.
  • Konjugovaný, Ak sa táto suma rovná 360 °.
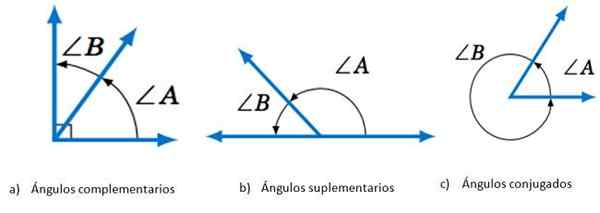Uhly podľa súčtu jej opatrení. Zdroj: matematické librettexts.

Pokiaľ ide o polohu ich strán, môžu byť dva uhly:

  • Za sebou, Keď má spoločný vrchol a jedna zo strán.
  • Susedný, Ak sú po sebe idúce, ale non -common strany sú opačné, takže sú tiež doplnkové.
  • Oproti vrcholu, Keď majú spoločný vrchol a strany uhlov sú predĺžené v opačnom smere.
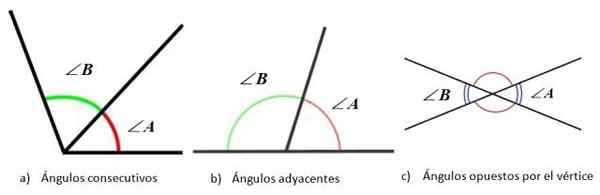Uhly podľa relatívnej polohy medzi jej stranami. Zdroj: f. Zapata

Trojuholníky

Trojuholník je plochá a uzavretá geometrická postava, ktorá patrí do rodiny polygónov, s tromi stranami zloženými z čiary, ktoré sú rezané dve až dve, a vytvárajú tri uhly.

Môže vám slúžiť: Bijjektívna funkcia: Čo je to, ako sa to robí, príklady, cvičenia

Jeho základné prvky sú:

  • Vrcholy, ktoré sú priesečníkmi vyššie uvedených línií.
  • Strany, celkom 3 a ktoré pozostávajú zo segmentov riadkov, ktoré sa pripájajú k vrcholom.
  • Vnútorné uhly, Tiež v počte 3, ktorých suma sa vždy rovná 180 °.

Všeobecne platí, že strany sú označené malými latinskými písmenami, vrcholmi s kapitálovými písmenami a uhlami s malými písmenami, ale sú možné aj ďalšie zápisy.

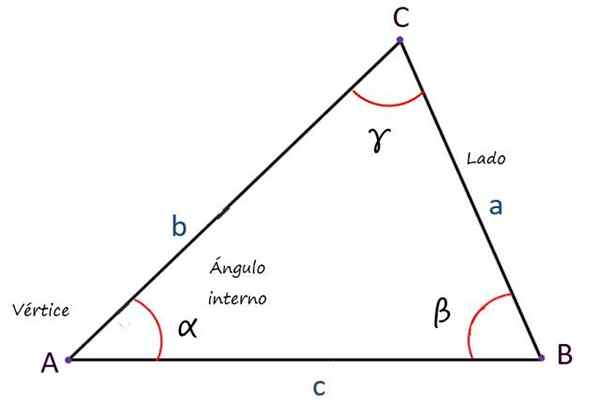Hlavné prvky trojuholníka. Zdroj: f. Zapata

Typy trojuholníkov

Trojuholníky podľa tvaru jeho strán

Podľa tohto kritéria môžu byť trojuholníky:

  • Rovnostranné prostriedky, Ak majú jeho tri strany rovnaké opatrenie.
  • Izoscely, Keď iba dve strany majú rovnakú mieru, zatiaľ čo tretí je iný.
  • Vyskakovať, Ak sú tieto tri strany rôzna veľkosť.
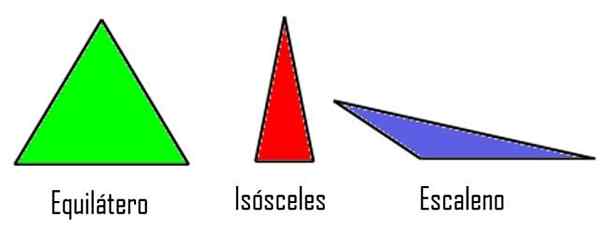Trojuholníky podľa ich strán. Upravené Wikimedia Commons

Trojuholníky podľa svojich vnútorných uhlov

Toto kritérium je založené na typoch vnútorných uhlov trojuholníka. Podľa toho môže byť trojuholník:

  • Akulógový, Keď sú tri vnútorné uhly trojuholníka akútne.
  • Obdĺžnik, Ak má trojuholník vnútorný uhol merania rovnajúci sa 90 °.
  • Tupý, Jeden z vnútorných uhlov trojuholníka je tupý.
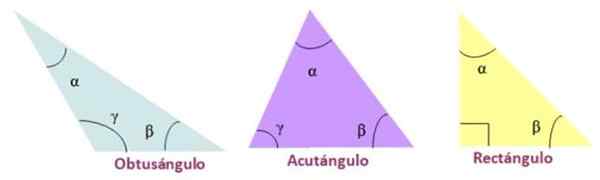Typy trojuholníka podľa jeho vnútorných uhlov. Zdroj: f. Zapata

Pozoruhodné segmenty trojuholníka

Medzi pozoruhodné segmenty akéhokoľvek trojuholníka majú:

  • Stredný, segment nasmerovaný zo vrcholu, priamo na opačnú stranu.
  • Mediacia, Je to segment patriaci k čiare kolmej na bok, ktorá sa pretína do stredu tejto strany.
  • Bisektor, Segment, ktorý rozdeľuje vnútorný uhol do dvoch rovnakých častí, a ktorý sa rozširuje na opačnú stranu k uhlu.
  • Výška, segment kolmo na stranu, ktorá siaha až po opačný vrchol.
Môže vám slúžiť: Lagrange Interpolácia

Tri stredné, tri mediácie je možné vysledovať a tak ďalej.

Trojuholník

V každom trojuholníku vynikajú nasledujúce body (pozri nasledujúci obrázok):

  • Baricentro g, Tiež sa niekedy volá stredobod z trojuholníka je to bod priesečníka mediánov a je vždy interiérom trojuholníka.
  • Ortocenter h, bod, v ktorom sa pretínajú tri výšky.
  • Ciruscentro alebo, Je to bod priesečníka mediácií. Nájdete ho mimo trojuholníka, ak je to tupé, zatiaľ čo v obdĺžnikovom trojuholníku alebo sa zhoduje so stredom hypotenusu.
  • Stimul, križovatka pre trojuholníkové bisektory.
  • Euler rovno, rovno, ktorý spája baricenter, ortocenter a Cicrecentro, v akomkoľvek trojuholníku, ktorý nie je rovnostranný. Vždy je splnené, že dĺžka segmentu Hg je dvojnásobná v segmente GO.
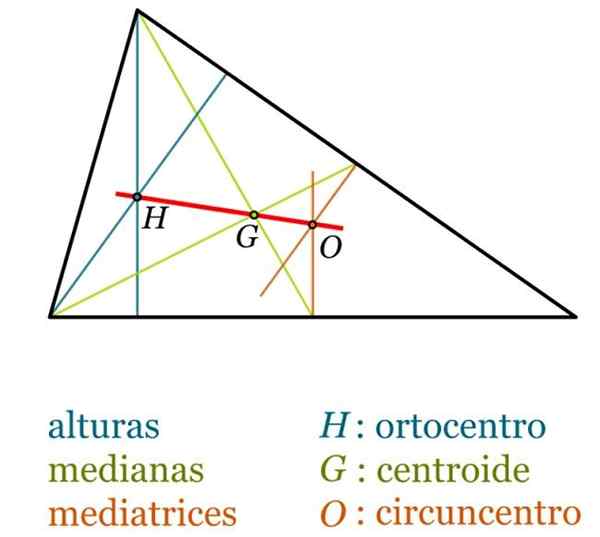Pozoruhodné body a segmenty trojuholníka. Zdroj: Wikimedia Commons

Plocha trojuholníka

Na výpočet oblasti A z trojuholníka sa používa nasledujúci vzorec všeobecnej povahy:

A = báza × výška / 2

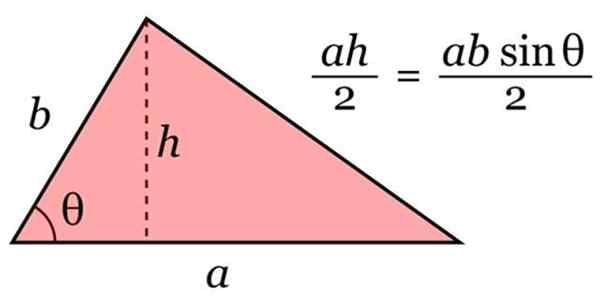Oblasť trojuholníka. Zdroj: Wikimedia Commons

Herón

Poznanie dĺžky všetkých strán trojuholníka, nasledujúceho vzorec, známy ako Herón, Umožňuje nájsť oblasť A:

Tu sú strany trojuholníka A, B a C, zatiaľ čo Sp je on polotumeter, to znamená, polovica obvodu p = a + b + c.

Odkazy

  1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
  2. Uhly. Matematické librettexts. Získané z: matematiky.Librettexts.orgán.
  3. Jiménez, René. 2010. Matematika II (geometria a trigonometria). Druhý. Vydanie. Pearson.
  4. Vesmír. Trojuholník. Získané z: Universoformulas.com.
  5. Zapata, f. Trojuholníky: História, prvky, klasifikácia, vlastnosti. Zdroj: Lifer.com.