Maďarská metóda, čo pozostáva, príklad

On Maďarská metóda Je to algoritmus, ktorý sa používa pri problémoch s prideľovaním, keď chcete minimalizovať náklady. To znamená, že sa používa na nájdenie minimálnych nákladov priradením niekoľkých ľudí k rôznym činnostiam na základe najnižších nákladov. Každá činnosť musí byť priradená inej osobe.

Problémom priradenia je špeciálny typ problému lineárneho programovania, kde cieľom je minimalizovať náklady alebo čas dokončenia množstva práce niekoľkými ľuďmi.

Zdroj: Pixabay.com

Jednou z dôležitých charakteristík problému prideľovania je, že iba jedna práca (alebo pracovník) je priradená k stroju (alebo projektu).

Túto metódu vyvinula maďarský matematik D. Konig. Z tohto dôvodu je známa ako maďarská metóda problémov s prideľovaním. Je tiež známy ako algoritmus priradenia Kuhn-Munkres.

Akýkoľvek problém pridelenia je možné ľahko vyriešiť použitím tejto metódy pozostávajúcej z dvoch fáz:

- Pri prvej fáze dochádza k zníženiu riadkov a zníženia stĺpcov.

- V druhej fáze je riešenie na iteračnej báze optimalizované.

[TOC]

Aká je maďarská metóda?

Maďarská metóda pozostáva zo štyroch krokov. Prvé dva kroky sa vykonávajú iba raz, zatiaľ čo kroky 3 a 4 sa opakujú, až kým nenájdu optimálne zadanie.

Považuje sa za vstupnú skutočnosť do štvorcovej matice objednávky n, ktorá musí obsahovať iba negatívne prvky.

Pre daný problém, ak sa počet riadkov v matrici nevyrovná počtu stĺpcov, musí sa pridať fiktívny riadok alebo fiktívny stĺpec, v závislosti od prípadu. Náklady na priradenie pre tieto fiktívne bunky sú vždy priradené ako nula.

Krok 1: Odčítajte minimá každého riadku

Pre každý riadok matice je prvok vybraný s najnižšou hodnotou a odčítaniami každého prvku v tomto riadku.

Môže vám slúžiť: Aký je súčasný majetok? (S príkladmi)

Krok 2: Odčítajte minimá každého stĺpca

Podobne je zvolený prvok s najnižšou hodnotou pre každý stĺpec a odčítať ho od každého prvku v tomto stĺpci.

Krok 3: Zakryte všetky nuly s minimálnym počtom riadkov

Všetky nuly musia byť zakryté v matrici vyplývajúcej z kroku 2 pomocou minimálneho počtu vodorovných a zvislých čiar, buď riadkami alebo stĺpcami.

Ak sú potrebné celkové riadky na pokrytie všetkých nulov, pričom n sa rovná veľkosti n za n matrice, medzi nulami bude optimálne priradenie, a preto sa algoritmus zastaví.

V opačnom prípade, ak sa vyžaduje menej riadkov na pokrytie všetkých nulov v matrici, pokračuje s krokom 4.

Krok 4: Vytvorte ďalšie nuly

Vybraný je najmenší prvok matice (nazývaný k), ktorý nie je pokrytý jednou z riadkov vyrobených v kroku 3.

Hodnota k všetkých prvkov, ktoré nie sú pokryté riadkami. Následne sa hodnota K pridá do všetkých prvkov, na ktoré sa vzťahuje križovatka dvoch riadkov.

Prvky, ktoré sú pokryté jedným riadkom, sú ponechané tak, ako sú. Po vykonaní tohto kroku sa vrátite do kroku 3.

Optimálne priradenie

Akonáhle je algoritmus zastavený v kroku 3, je zvolená sada nulov, takže každý riadok a každý stĺpec má iba jeden zvolený nula.

Ak v tomto výberovom procese nie je v rade alebo stĺpci jediná nula, potom bude vybraný jeden z týchto nulov. V tomto stĺpci alebo riadku sú vylúčené zostávajúce nuly, ktoré sa opakujú aj pre ostatné úlohy.

Môže vám slúžiť: makrolokalizácia

Ak neexistuje jediné pridelenie nulov, znamená to, že existuje viac riešení. Náklady však zostanú rovnaké pre rôzne súpravy alokácie.

Akýkoľvek fiktívny riadok alebo stĺpec, ktorý bol pridaný. Nuly vybrané v tejto konečnej matrici zodpovedajú ideálnemu priradeniu požadovanej v pôvodnej matrici.

Príklad

Zvážte spoločnosť, v ktorej existujú štyri aktivity (A1, A2, A3, A4), ktoré musia vykonávať štyria pracovníci (T1, T2, T3, T4). Musí byť pridelená činnosť na pracovníka.

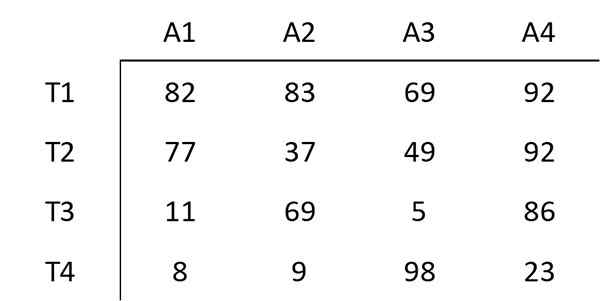
Nasledujúca matica ukazuje náklady na priradenie určitého pracovníka k určitej činnosti. Cieľom je minimalizovať celkové náklady na úlohu zloženú z týchto štyroch činností.

Krok 1: Odčítajte minimá každého riadku

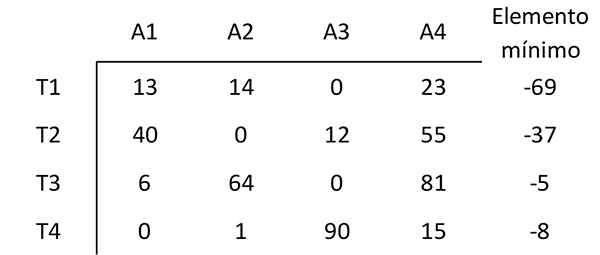
Prvok začína minimálnou hodnotou každého riadku ostatných prvkov tohto riadku. Napríklad najmenší prvok v prvom riadku je 69. Preto sa v prvom riadku odpočítava 69 každého prvku. Výsledná matica je:

Krok 2: Odčítajte minimá každého stĺpca

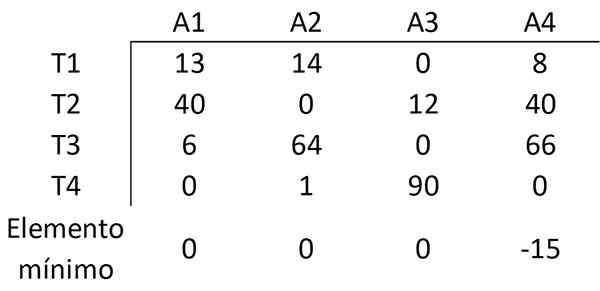
Rovnakým spôsobom sa prvok odpočíta s minimálnou hodnotou každého stĺpca ostatných prvkov tohto stĺpca a získajú nasledujúcu maticu:

Krok 3: Zakryte všetky nuly s minimálnym počtom riadkov

Teraz bude stanovený minimálny počet riadkov (horizontálne alebo vertikálne), ktoré sú potrebné na pokrytie všetkých nulov v matrici. Všetky nuly môžu byť zakryté pomocou 3 riadkov:

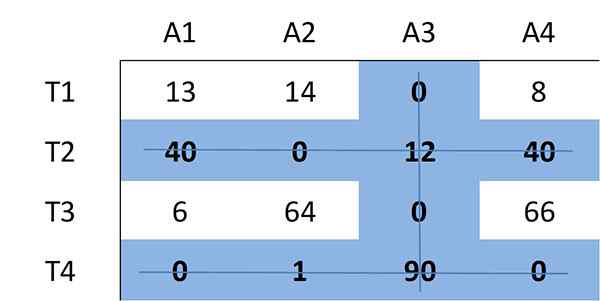
Pretože počet požadovaných riadkov je tri a je menší ako veľkosť matice (n = 4), pokračuje s krokom 4.

Môže vám slúžiť: Projektové riadenie: Čo je, fázy, ciele, príklady

Krok 4: Vytvorte ďalšie nuly

Najnižší prvok, ktorý nie je zakrytý riadkami, je vybraný, ktorého hodnota je 6. Táto hodnota všetkých nekercovitých prvkov sa odpočíta a rovnaká hodnota sa pridáva k všetkým prvkom, na ktoré sa vzťahuje križovatka dvoch riadkov. To má za následok nasledujúcu maticu:

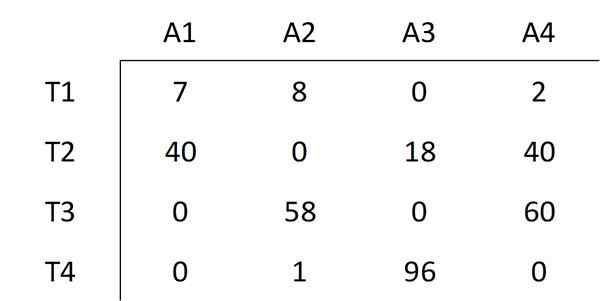
Ako je uvedené v maďarskej metóde, musí sa znova vykonať krok číslo tri.

Krok 3 (opakovanie)

Opäť je určený minimálny počet riadkov potrebných na pokrytie všetkých nulov v matrici. Tentoraz sú potrebné štyri riadky:

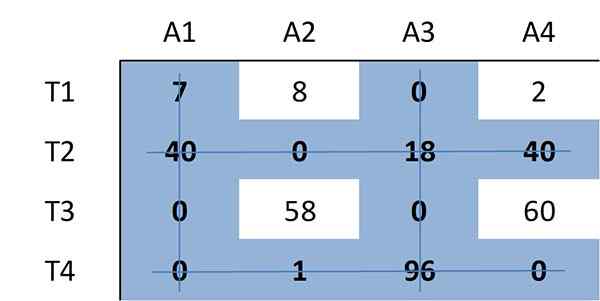
Pretože počet požadovaných riadkov je 4, rovná sa veľkosti matice (n = 4), v matrici je optimálne priradenie medzi Zeros. Preto sa algoritmus zastaví.

Optimálne priradenie

Ako je uvedené v metóde, výber z nasledujúcich nulov zodpovedá optimálnemu priradeniu:

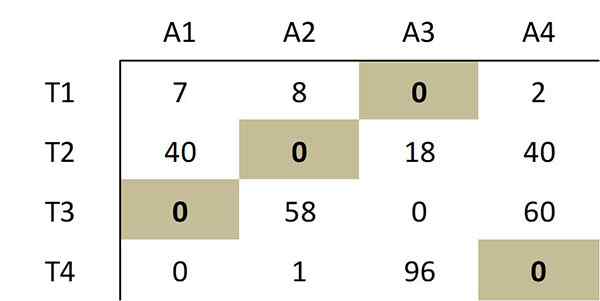
Tento výber nuly zodpovedá nasledujúcemu optimálnemu rozdeleniu v pôvodnej matici nákladov:

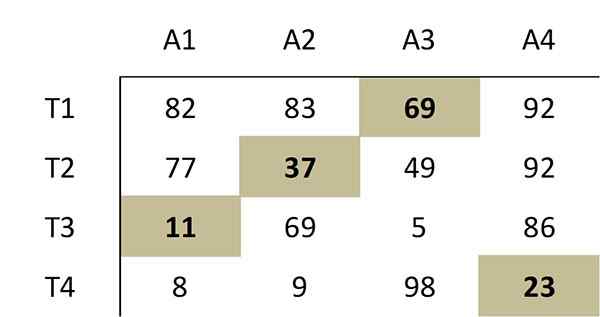
Preto musí pracovník 1 vykonávať činnosť 3, pracovník 2, aktivita 2, pracovník 3, aktivita 1 a pracovník 4 musia vykonať aktivitu 4. Celkové náklady na toto optimálne priradenie je 69+37+11+23 = 140.

Odkazy

1. Maďarský algoritmus (2019). Algoritmus Maďarska. Zobraté: Maďarianalgoritmus.com.
2. Štúdia (2019). Použitie algoritmu Maďarska na riešenie problémov s priradením. Zobraté z: štúdie.com.
3. Pracovné miesta (2018). Maďarská metóda na riešenie problému priradenia - kvantitatívne techniky riadenia. Prevzaté z: múdrosti.com.
4. Geeks for Geeks (2019). Maďarský algoritmus pre problém s priradením. Prevzaté z: Geeksforgeeks.orgán.
5. Karleight Moore, Nathan Landman (2019). Maďarsko maximálny zodpovedajúci algoritmus. Brilantný. Prevzaté: brilantné.orgán.