Eulerova metóda pre to, čo je použitie postupu a cvičení

On Eulerová metóda Je to najzákladnejšia a najjednoduchšia z postupov používaných na nájdenie približných numerických riešení v bežnej diferenciálnej rovnici prvého poriadku za predpokladu, že jeho počiatočný stav je známy.

Bežná diferenciálna rovnica (EDO) je rovnica, ktorá súvisí s neznámou funkciou jednej nezávislej premennej s jej derivátmi.

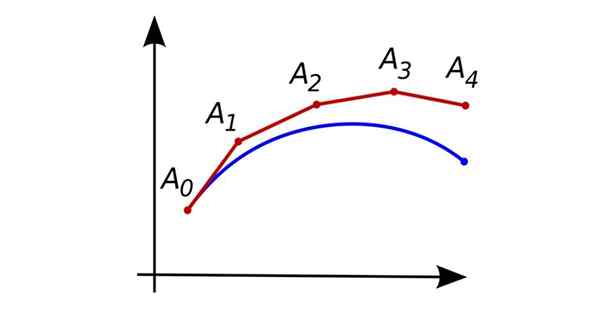
Postupné prístupy Eulerovou metódou. Zdroj: Oleg Alexandrov [verejná doména]

Ak je najväčší derivát, ktorý sa objaví v rovnici, z prvého stupňa, potom je to obyčajná diferenciálna rovnica prvého stupňa.

Najbežnejším spôsobom písania rovnice prvého stupňa je:

s počiatočnou podmienkou:

x = x₀

y = y₀

[TOC]

Aká je Eulerova metóda?

Myšlienka Eulerovej metódy je nájsť numerické riešenie diferenciálnej rovnice v intervale medzi x₀ a x_F .

Po prvé, interval v n+1 bodoch je nesúhlasný:

X₀, X₁, X₂, X₃…, X_n

Ktoré sa získavajú takto:
X_Jo= x₀+IH

Kde h je šírka alebo krok subintervalov:

Čím väčšie je počet n, výsledok bude presnejší, ale na pokrytie intervalu, kde hľadáme riešenie, bude potrebný väčší počet bodov.

S počiatočnou podmienkou je možné na začiatku poznať derivát:

a '(x_ani) = f (x_ani, a_ani)

Tento derivát predstavuje sklon čiary dotykovej do funkčnej krivky y (x) presne v bode:

AO = (x_ani, a_ani)

Potom sa v nasledujúcom bode uskutoční približná predpoveď hodnoty funkcie y (x):

a (x₁) ≈ a₁

a_1 = a_ani +(X₁- X_ani) f (x_ani, a_ani) = y_{ani +} H F (x_ani, a_ani)

Ďalší približný bod riešenia, ktorý by zodpovedal:

Do₁ = (x₁, a₁)

Postup sa opakuje, aby sa získali následné body

Môže vám slúžiť: Logaritmická funkcia: Vlastnosti, príklady, cvičenia

Do₂, Do₃…, X_n

Na obrázku znázornenom na začiatku predstavuje modrá krivka presné riešenie diferenciálnej rovnice a červená predstavuje následné približné body získané Eulerovou postupom.

Vyriešené cvičenia

Cvičenie 1

Jo) Byť diferenciálnou rovnicou:

S počiatočnou podmienkou x = a = 0; a_do= 1

Použitím metódy Eulera získajte približné riešenie a V súradnici x = b = 0.5, rozdelenie intervalu [a, b] v n = 5 častí.

Riešenie

Numerické výsledky sú zhrnuté takto:

Kde sa dospelo k záveru, že riešenie a hodnota 0.5 je 1.4851.

Poznámka: Na realizáciu výpočtov, ktoré sa použila Štúdio Smath, Program bezplatného použitia zadarmo.

Cvičenie 2

Ii) Pokračujte v diferenciálnej rovnici cvičenia i), nájdite presné riešenie a porovnajte ho s výsledkom získaným metódou Eulerovej metódy. Nájdite chybu alebo rozdiel medzi presným výsledkom a približným výsledkom.

Riešenie

S počiatočnou podmienkou x = a = 0; a_do= 1
Presné riešenie nie je príliš ťažké nájsť. Je známe, že derivát funkcie Sen (X) je funkcia cos (x). Preto riešenie y (x) bude:

a (x) = sin x + c

Na splnenie počiatočnej podmienky a (0) = 1, konštanta C musí mať hodnotu 1. Ďalej sa porovnáva presný výsledok s približným:

Dospelo sa k záveru, že v vypočítanom intervale má prístup tri významné údaje o presnosti.

Cvičenie 3

Iii) Zvážte diferenciálnu rovnicu a jej počiatočné podmienky uvedené nižšie:

a '(x) =- y²

S počiatočnou podmienkou x₀ = 0; a₀ = 1

Použite metódu Eulera na nájdenie približných hodnôt riešenia a (x) V intervale x = [0, 1.5]. Použiť krok H = 0.1.

Riešenie

Eulerova metóda je veľmi naznačená, že sa používa s tabuľkou. V tomto prípade použijeme tabuľku Geogebra, Program bezplatného a bezplatného použitia.

Môže vám slúžiť: Zložená proporcionalita: Vysvetlenie, tri zložené pravidlo, cvičenia

V tabuľke obrázku sú znázornené tri stĺpce (A, B, C) X , Druhý stĺpec predstavuje premennú a, a tretí stĺpec derivát a '.

Riadok 2 obsahuje počiatočné hodnoty X, A, A ' .

Hodnota hodnoty 0.1 bol umiestnený v absolútnej pozícii bunky ($ D 4).

Počiatočná hodnota Y0 je v bunke B2 a Y1 v bunke B3. Vypočítať a₁ Používa sa vzorec:

a_1 = a_ani +(X₁- X_ani) f (x_ani, a_ani) = y_{ani +} H F (x_ani, a_ani)

Tento tabuľkový vzorec by bolo číslo B3: = B2 + $ D $ 4 * C3.

Podobne by bol Y2 v bunke B4 a jeho vzorec je znázornený na nasledujúcom obrázku:

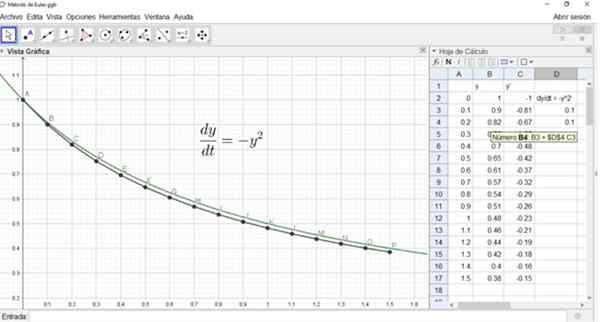
Obrázok tiež ukazuje graf presného riešenia a body A, B, ..., P približného roztoku pomocou metódy Eulerovej metódy.

Newton Dynamics a Eulerova metóda

Klasical Dynamics vyvinula Isaac Newton (1643 - 1727). Pôvodná motivácia Leonarda Eulera (1707 - 1783) na vývoj jeho metódy bolo presne vyriešiť rovnicu Newtonovho druhého zákona v rôznych fyzických situáciách.

Newtonov druhý zákon sa často vyjadruje ako sekundárna diferenciálna rovnica:

Kde X Momentálne predstavuje polohu objektu tón. Tento objekt má hmotnosť m a je vystavený sile F. Funkcia F Súvisí s silou a hmotnosťou nasledovne:

 Aj keď bola metóda Eulera v zásade navrhnutá na riešenie prvých diferenciálnych rovníc, je ľahko rozšíriteľná v prípade druhého degrea, pretože je rovnocenná s systémom dvoch prvých rovníc prvých degrea.

Môže vám slúžiť: analytická geometria

Na použitie metódy Eulera sú potrebné počiatočné časové hodnoty tón, rýchlosť vložka a pozícia X.

Nasledujúca tabuľka vysvetľuje, ako je možné získať počiatočné hodnoty T1, V1, X1 Aproximácia rýchlosti V2 a polohy X2, v okamihu T2 = T1+AT, kde AT predstavuje malé zvýšenie a zodpovedá kroku v metóde Eulera.

Cvičenie 4

Iv) Jedným zo základných problémov v mechanike je problém s hmotnosťou zviazanou na pružinu (alebo pružinu) elastickej konštanty K.

Newtonov druhý zákon pre tento problém by bol taký:

V tomto príklade sa na jeho zjednodušenie urobí m = 1 a k = 1. Nájdite približné riešenia polohy X A rýchlosť vložka Eulerovou metódou v časovom intervale [0, π/2] rozdelenie intervalu v 12 dieloch.

Vezmite 0 ako počiatočný moment, počiatočná rýchlosť 0 a počiatočná poloha 1.

Riešenie

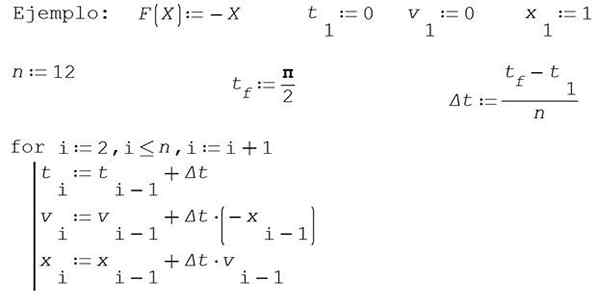
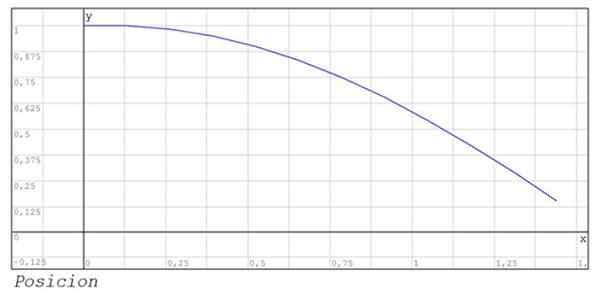
Numerické výsledky sú uvedené v nasledujúcej tabuľke:

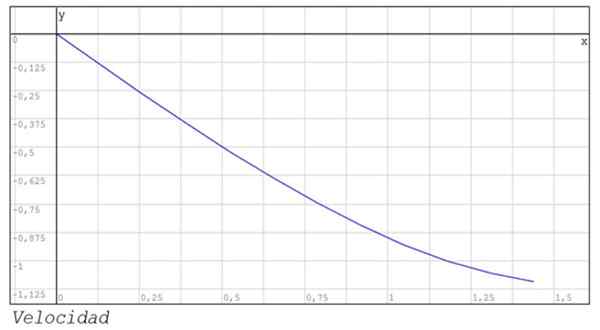
Zobrazuje sa aj grafika polohy a rýchlosť medzi inštanciami 0 a 1.44.

Navrhované cvičenia pre dom

Cvičenie 1

Použite tabuľku na určenie približného riešenia pomocou metódy Eulera pre diferenciálnu rovnicu:

a '= -exp (-y) s počiatočnými podmienkami x = 0, y = -1 v intervale x = [0, 1]

Začnite s krokom 0,1. Graf výsledku.

Cvičenie 2

Použitím tabuľky nájdite numerické riešenia nasledujúcej rovnice druhého stupňa, kde a je to funkcia nezávislej premennej t.

a "= - 1/y² s počiatočnou podmienkou t = 0; y (0) = 0,5; a '(0) = 0

Nájdite roztok v intervale [0,5; 1.0] pomocou kroku 0,05.

Graf Výsledok: a vs t; a 'vs t

Odkazy

1. Eurlerov metóda.Prevzaté z Wikipédie.orgán
2. Riešiteľ Eulera. Prevzatý.Hanba.com