Pertilineárne charakteristiky pohybu, typy a príklady

On priamy pohyb Je to jeden, v ktorom sa mobilný pohyb pohybuje po priamke, a preto prechádza v dimenzii, a preto dostáva názov Jednosmerný pohyb. Táto priamka je trajektória alebo cesta nasledovaná objektom, ktorý sa pohybuje. Autá cestujúce pozdĺž cesty na obrázku 1 sledujú tento typ pohybu.

Toto je najjednoduchší model pohybu, ktorý si môžete predstaviť. Denné pohyby ľudí, zvierat a vecí často kombinujú prevody v priamke s pohybmi pozdĺž kriviek, ale niektoré často pozorujú niektoré, ktoré sú výlučne rektilineálne.

postava 1. Autá pohybujúce sa pozdĺž priamočiary. Zdroj: Pixabay.

Tu je niekoľko dobrých príkladov:

- Pri behu pozdĺž 200 -metrovej priamej trati.

- Vedenie auta na rovnej ceste.

- Voľne spadnúť objekt z určitej výšky.

- Keď sa lopta hodí zvisle.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Cieľ opisu pohybu sa teraz dosiahne špecifikáciou charakteristík, ako napríklad:

- Pozícia

- Posunutie

- Rýchlosť

- Zrýchlenie

- Čas.

Aby pozorovateľ detegoval pohyb objektu, je potrebné mať referenčný bod (pôvod O) a stanovil konkrétnu adresu, v ktorej sa má pohybovať, ktorá môže byť osou X, os a alebo akýkoľvek iný.

Pokiaľ ide o objekt, ktorý sa pohybuje, môže to mať nespočetné množstvo spôsobov. V tomto ohľade neexistujú žiadne obmedzenia, avšak vo všetkom, čo nasleduje, sa predpokladá, že mobil je časticou; Objekt taký malý, že jeho rozmery nie sú relevantné.

Je známe, že to tak nie je prípad makroskopických objektov; Je to však model s dobrými výsledkami v opise globálneho pohybu objektu. Týmto spôsobom môže byť časticou auto, planéta, osoba alebo akýkoľvek iný objekt, ktorý sa pohybuje.

Začneme štúdium rektilineárnej kinematiky so všeobecným prístupom k hnutiu a potom sa budú študovať konkrétne prípady ako tie, ktoré už boli vymenované.

[TOC]

Všeobecné charakteristiky priameho pohybu

Nasledujúci popis je všeobecný a uplatňuje sa na akýkoľvek typ jedného -rozmerového pohybu. Prvá vec je zvoliť referenčný systém. Čiara, po ktorej sa pohyb uskutoční, bude os X. Parametre pohybu:

Pozícia

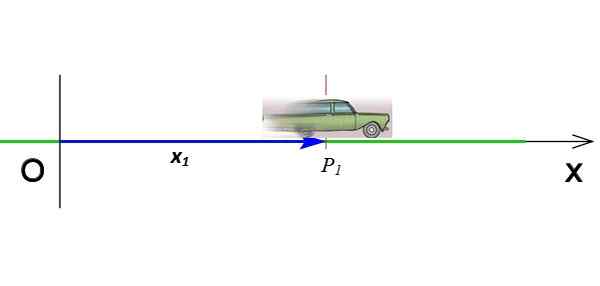Obrázok 2. Poloha mobilu, ktorý sa pohybuje na osi x. Zdroj: Wikimedia Commons (modifikované podľa F. Zapata).

Je to vektor, ktorý prechádza z pôvodu do bodu, keď je objekt v okamžitom okamihu. Na obrázku 2 vektor X₁ Označuje polohu mobilu, keď je v súradnici P₁ a včas tón₁. Vektorové jednotky v medzinárodnom systéme sú meracie výrobky.

Posunutie

Posun je vektor, ktorý označuje zmenu polohy. Na obrázku 3 auto prešlo z pozície P₁ do pozície P₂, Preto je jeho posunutie ΔX = X₂ - X₁. Posun je odčítanie dvoch vektorov, je symbolizované gréckym písmenom δ („delta“) a je zase vektorom. Jeho jednotky v medzinárodnom systéme sú meracie výrobky.

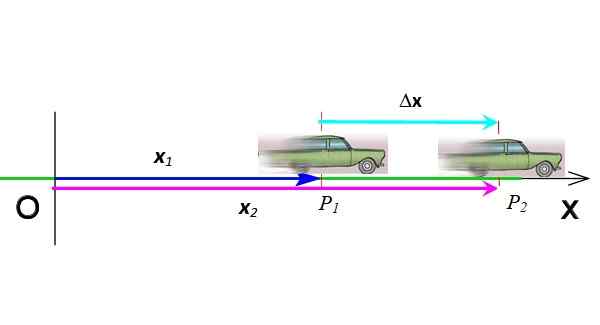Obrázok 3. Vektorový posun. Zdroj: Pripravený F. Zapata.

Vektory sú označené tučným písmom v tlačenom texte. Ale byť v rovnakej dimenzii, ak je to potrebné.

Môže vám slúžiť: pobočky klasickej a modernej fyziky

Prešiel

Vzdialenosť d Prehliadka pohybujúcim sa objektom je absolútnou hodnotou vektora posunu:

D = ΙXΙ = δX

Keďže je absolútna hodnota, prejdená vzdialenosť je vždy väčšia alebo rovná 0 a jej jednotky sú rovnaké ako jednotky polohy a posunu. Absolútna notácia hodnoty je možné vykonať pomocou stĺpcov modulov alebo jednoduchým odstránením výrazného písmena v tlačenom texte.

Priemerná rýchlosť

Ako rýchlo sa mení pozícia? Existujú pomalé a rýchle mobilné telefóny. Kľúčom bola vždy rýchlosť. Na analýzu tohto faktora sa analyzuje pozícia X funkcia času tón.

Priemerná rýchlosť vložka_m (Pozri obrázok 4) Je to sklon sušiacej čiary (fuchsia) k krivke X vs tón a poskytuje globálne informácie o mobilnom posunu v zvažovanom časovom intervale.

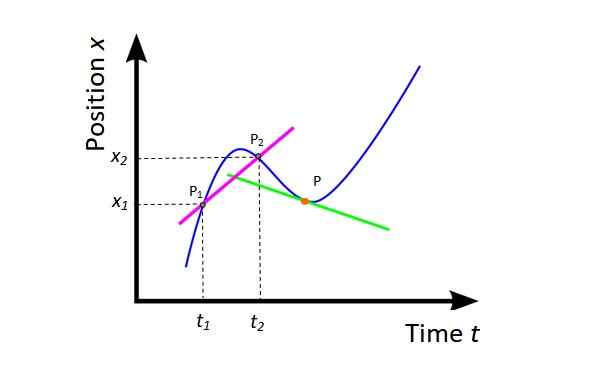Obrázok 4. Priemerná rýchlosť a okamžitá rýchlosť. Zdroj: Wikimedia Commons, upravené f. Zapata.

vložka_m = (X₂ - X₁) / (t₂ -tón₁) = ΔX / Δtón

Priemerná rýchlosť je vektor, ktorého jednotky v medzinárodnom systéme sú metre /druhé (pani).

Okamžitá rýchlosť

Priemerná rýchlosť sa počíta pomocou merateľného časového intervalu, ale neinformuje o tom, čo sa deje v uvedenom intervale. Ak chcete poznať rýchlosť kedykoľvek, musíte urobiť časový interval veľmi malý, matematicky je to rovnocenné s:

ΔT → 0

Rovnica je predtým uvedená pre priemernú rýchlosť. Týmto spôsobom sa získa okamžitá rýchlosť alebo jednoducho rýchlosť:

Geometricky je derivát polohy vzhľadom X vs tón v danom bode. Na obrázku 4 je bod oranžový a dotyčnica je zelená. Okamžitá rýchlosť v tomto bode je sklon tejto čiary.

Rýchlosť

Rýchlosť je definovaná ako modul absolútnej hodnoty alebo rýchlosti a je vždy pozitívny (signalizácia, cesty a diaľnice sú vždy pozitívne, nikdy negatívne). Pojmy „rýchlosť“ a „rýchlosť“ sa môžu používať denne, ale vo fyzike je rozdiel medzi vektorom a lezením potrebné.

vložka = ΙvložkaΙ = vložka

Priemerné zrýchlenie a okamžité zrýchlenie

Rýchlosť sa môže v priebehu pohybu zmeniť a realita je taká, že sa očakáva, že tak urobí. Existuje veľkosť, ktorá kvantifikuje túto zmenu: zrýchlenie. Ak si všimneme, že rýchlosť je zmena polohy vzhľadom na čas, zrýchlenie je zmena rýchlosti vzhľadom na čas.

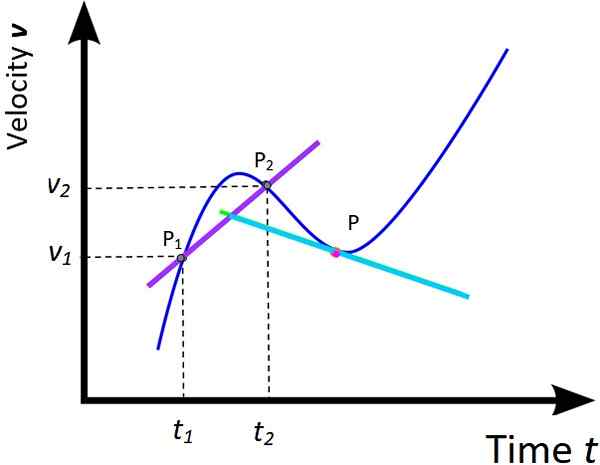Obrázok 5. Priemerné zrýchlenie a okamžité zrýchlenie. Zdroj: Wikimedia Commons, upravené f. Zapata.

Ošetrenie pridelené grafu X vs tón z dvoch predchádzajúcich oddielov možno rozšíriť na zodpovedajúci graf vložka vs tón. V dôsledku toho sú priemerné zrýchlenie a okamžité zrýchlenie definované ako:

do_m = (vložka₂ - vložka₁) / (t₂ -tón₁) = Δvložka / Δtón  (Do príbytku)

Zrýchlenie a spomalenie

V jednom -rozmernom pohybe majú vektory podľa dohovoru pozitívne alebo negatívne príznaky, ktoré idú tak či onak. Keď má zrýchlenie rovnaký význam ako rýchlosť, zvyšuje sa jeho veľkosť, ale keď dáva opačný zmysel a rýchlosť znižuje jeho veľkosť. Potom sa hovorí, že pohyb je oneskorený.

Môže vám slúžiť: Leyden fľaša: časti, prevádzka, experimenty

Chlapci

Klasifikácia rektilínskych pohybov sa zvyčajne vykonáva na základe:

- Či je zrýchlenie konštantné alebo nie.

- Pohyb prechádza pozdĺž vodorovnej alebo vertikálnej čiary.

Pohyb s neustálym zrýchlením

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Ak je zrýchlenie konštantné, priemerné zrýchlenie do_m Je to rovnaké ako okamžité zrýchlenie do A existujú dve možnosti:

- Že zrýchlenie má hodnotu 0, v takom prípade je rýchlosť konštantná a má rovnomerný priamy pohyb alebo MRU.

- Konštantné zrýchlenie odlišné od 0, v ktorom rýchlosť rastie alebo v priebehu času lineárne znižuje (rektilineárny pohyb rovnomerne sa mení alebo MRUV):

Kde vložka_F  a tón_F Sú konečnou rýchlosťou a časom, a vložka_ani a tón_ani Sú počiatočná rýchlosť a čas. Jo tón_ani = 0, Pri vymazaní konečnej rýchlosti máte rovnicu už známu pre konečnú rýchlosť:

vložka_F = v_ani + Na

Pre tento pohyb sú platné aj nasledujúce rovnice:

- Pozícia v závislosti od času: x = x_ani + vložka_{ani .}t +½ o²

- Rýchlosť v závislosti od polohy: vložka_F² = v_ani² + Druhý.ΔX  (S δx = x - x_ani)

Vodorovné pohyby a vertikálne pohyby

Horizontálne pohyby sú tie, ktoré prechádzajú pozdĺž vodorovnej osi alebo osi x, zatiaľ čo vertikálne to robia pozdĺž osi a osi. Vertikálne pohyby pod pôsobením gravitácie sú najčastejšie a najzaujímavejšie.

V predchádzajúcich rovniciach sa berie A = g = 9.8 m/s² smerovaný vertikálne nadol, smer, ktorý je takmer vždy vybraný s negatívnym znakom.

Tadiaľto, vložka_F = v_ani + Na Transformuje sa v vložka_F = v_ani - Gt A ak je počiatočná rýchlosť 0, pretože objekt bol voľne klesnutý, je ďalej zjednodušené vložka_F = - gt. Pokiaľ sa samozrejme nezohľadňuje odpor vzduchu.

Vyriešené príklady

Príklad 1

V bode sa uvoľní malý balík tak, aby sa pohyboval pozdĺž transportéra s posuvnými kolesami ABCD zobrazenými na obrázku. Zatiaľ čo zostupuje cez naklonené sekcie AB a CD, balík nesie zrýchlenie 4,8 m/s², zatiaľ čo v horizontálnej časti BC udržiava konštantnú rýchlosť.

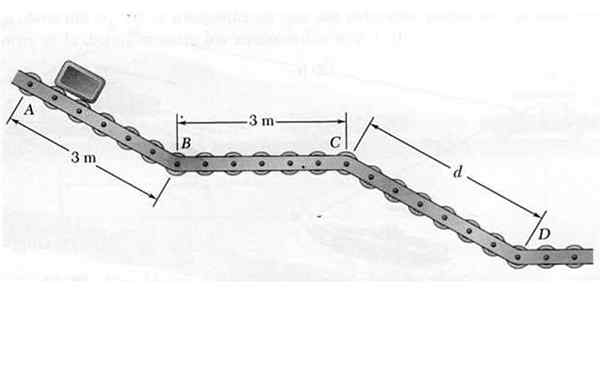Obrázok 6. Balík, ktorý sa pohybuje po posuvnej ceste vyriešeného príkladu 1. Zdroj: Self Made.

Vedieť, že rýchlosť, s akou je balenie v D dosahu, je 7,2 m/s, určte:

a) vzdialenosť medzi C a D.

b) čas potrebný na dosiahnutie konca balíka.

Riešenie

Pohyb balíka sa vykonáva v troch zobrazených rektilových častiach a na výpočet požadovanej rýchlosti je potrebná rýchlosť v bodoch B, C a D. Analyzme každú časť osobitne:

Sekcia AB

Pretože čas nie je k dispozícii v tejto časti, bude sa používať vložka_F² = v_ani² + Druhý.ΔX  S VO = 0:

vložka_F² = 2a.ΔX → vložka_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → vložka_F  = 5.37 m/s = v_B

Čas, ktorý balenie potrebuje na cestovanie sekcie AB, je:

tón_AB = (v_F - vložka_ani) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Sekcia BC

Rýchlosť v časti BC je preto konštantná vložka_B = v_C = 5.37 m/s. Čas potrebný na cestovanie balíka v tejto časti je:

Môže vám slúžiť: Light Rafrakt: prvky, zákony a experimenty

tón_Bc = vzdialenosť _Bc  / v_B = 3 m/ 5.37 m/s = 0.56 s

CD sekcia

Počiatočná rýchlosť tejto časti je vložka_C = 5.37 m/s, Posledná rýchlosť je vložka_D = 7,2 m/s, cez vložka_D²  = v_C² + 2. do. d Hodnota d:

D = (vložka_D²  - vložka_C²)/2.a = (7.2²  - 5.37²)/2 X 4.8 m = 2.4 m

Čas sa počíta ako:

tón_{Cd =} (v_D  - vložka_C)/A = (7,2-5.37)/ 4.8 s = 0.38 s.

Odpovede na nastolené otázky sú:

a) d = 2.4 m

b) Čas cesty je tón_AB + tón_Bc + tón_CD = 1.19 S +0.56 S +0.38 s = 2.13 s.

Príklad 2

Osoba je pod horizontálnou bránou, ktorá je pôvodne otvorená a vysoká 12 m. Osoba vertikálne spúšťa objekt smerom k bráne s rýchlosťou 15 m/s.

Je známe, že brána sa uzatvára 1,5 sekundy po tom, čo osoba spustila objekt z výšky 2 metre. Vzduchový odpor sa nezohľadňuje. Odpovedzte na nasledujúce otázky a odôvodnite:

a) Podarí sa vám odovzdať objekt cez bránu skôr, ako sa zatvorí?

b) Zráža sa predmet proti uzavretej bráne? Ak je kladné, kedy sa to stane?

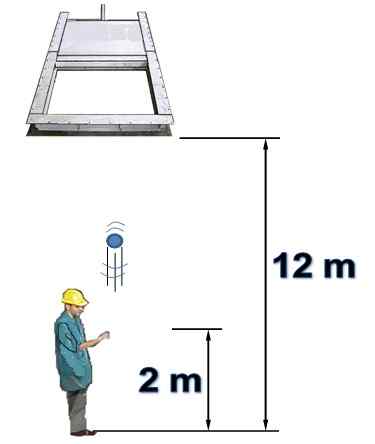Obrázok 7. Objekt sa spustí vertikálne nahor (vyriešený príklad 2). Zdroj: Self Made.

Odpoveď na)

Medzi počiatočnou polohou lopty a bránou je 10 metrov. Je to vertikálne spustenie, v ktorom sa táto adresa považuje za pozitívnu.

Pri príchode k tomuto bodu nájdete rýchlosť, ktorú nesie, s týmto výsledkom je čas, ktorý by to urobil a porovnal ju s časom uzávierky brány, čo je 1.5 sekúnd:

vložka_F ²= v_ani ²- 2.g. Δa → vložka_F = (15² - 2 X 9.8 X10)^1/2 m = 5.39 m/s

T = (v_F - vložka_ani) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Pretože tento čas je menší ako 1.5 sekúnd, potom sa dospelo k záveru, že objekt môže prejsť bránom aspoň raz.

Odpoveď b)

Už vieme, že objekt spravuje. Rýchlosť, keď siaha vo výške brány, má rovnakú veľkosť ako keď stúpa, ale v opačnom smere. Preto pracujte s -5.39 m/s a čas potrebný na dosiahnutie tejto situácie je:

T = (v_F - vložka_ani) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Pretože brána zostáva otvorená iba pre 1.5 s, je zrejmé, že nemá čas prejsť skôr, ako sa uzavrie, pretože zistí, že je uzavretý. Odpoveď znie: Objekt, ak sa zrazí so uzavretou bránou po 2.08 sekúnd po prepustení, keď príde v zostupe.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).69-116.
2. Giancoli, D. Fyzika. (2006). Zásady s aplikáciami. 6^th Vydanie. Sála. 22-25.
3. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 23 - 27.
4. Resnick, r. (1999). Fyzický. Zväzok 1. Tretie vydanie v španielčine. Mexiko. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 21-22.
5. Rex, a. (2011). Základy fyziky. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14^th. Edimatizovať. Zväzok 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Vydanie. Mexiko. Redaktori učenia sa Cengage. 23-25.
8. Serway, r., Vulle, C. (2011). Základy fyziky. 9^nat Edimatizovať. Učenie sa. 43 - 55.
9. Wilson, J. (2011). Fyzika 10. Pearson Vzdelanie. 133 - 149.