Rovnomerný kruhový pohyb (m.C.Alebo.) vzorce, charakteristiky

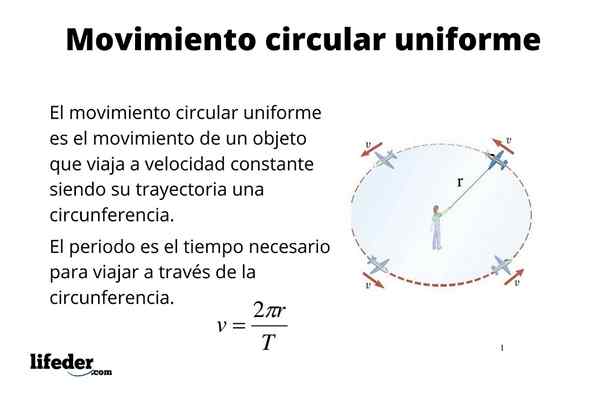
Častica má kruhový pohyb jednotný (M.C.Alebo.) Ak je jej trajektóriou obvodom a tiež ju tiež cestuje. Mnohé predmety, ako sú kúsky strojov a motorov, majú napríklad tento druh pohybu, medzi ktorými sú tvrdé disky počítačov, fenatre, sekery a mnoho ďalších vecí viac.

Rovnomerný kruhový pohyb je tiež dobrým prístupom k pohybu niektorých nebeských telies, ako je napríklad Zem. Zemská obežná dráha je skutočne eliptická, ako zdôrazňujú Keplerove zákony. Excentricita obežnej dráhy je však malá a ako prvý prístup sa môže považovať za kruhový, čo zjednodušuje niektoré výpočty, napríklad nájdenie rýchlosti Zeme, keď sa pohybuje okolo slnka.

V opise rovnomerného pohybu kruhového pohybu sa používajú rovnaké parametre ako v priamom pohybe, konkrétne: poloha, posun, čas, rýchlosť a zrýchlenie.

Zrýchlenie? Áno, v skutočnosti je rovnomerný kruhový pohyb zrýchlený, aj keď je jeho rýchlosť vložka byť konštantný. Je to preto, že rýchlosť vložka, Že je to vektor, a preto je tučným písmom, neustále mení svoj smer, keď sa objekt alebo častice otáčajú. Akákoľvek zmena v vložka Vytvára sa zrýchlením, ktoré bude vidieť, je nasmerované do stredu kruhovej trajektórie.

Rovnomerný kruhový pohyb je pohyb v rovine Xy, Preto je to dvojrozmerný pohyb. Je však možné pohodlnejšie vyjadriť uhlom 9, ktorý zametá častice, meranú vzhľadom na horizontálnu os alebo inú vhodnú referenčnú osi.

Aj keď ide o rozšírený objekt, jeho častice vždy zametajú rovnaký uhol, aj keď majú rôzne súradnice (X, y).

[TOC]

Charakteristiky rovnomerného kruhového pohybu

Môžete zhrnúť charakteristiky rovnomerného kruhového pohybu nasledovne:

-Trajektória je obvod, preto ide o pohyb v rovine.

-Rýchlosť vložka Je konštantná, ale rýchlosť vložka Nie, pretože neustále mení smer a význam, ktorý by vyhovoval mobilu.

-Vektor rýchlosti vložka Je to vždy tangenciálne k obvodu a kolmo na radiálny smer.

-Uhlová rýchlosť Ω je konštantná.

-Napriek tomu, že je jednotný, existuje zrýchlenie na vysvetlenie týchto zmien v smere rýchlosti. Toto zrýchlenie je centripetálne zrýchlenie.

-Centripetálne zrýchlenie a rýchlosť sú navzájom kolmé.

-Je to pravidelný alebo opakujúci sa pohyb, preto pre neho sú definované obdobie a frekvencia veľkosti a frekvencia.

Rovnomerné vzorce kruhového pohybu

V tejto schéme je P rotácie častíc P vložka nakreslený.

Môže vám slúžiť: Magnetické pole Zeme: pôvod, charakteristiky, funkcia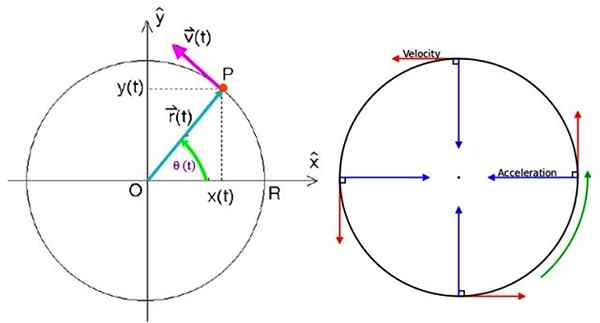 Rovnomerné parametre pohybu kruhového pohybu. Zdroj: f. Zapata/Wikimedia Commons.

Na zadanie vektora polohy je potrebné.

Vektor

Označuje sa ako r (t) a je nasmerovaný od pôvodu do bodu P, kde sa častica umiestnila. V okamžitom vzhľade T, v karteziánskych súradniciach, je napísaný ako:

r (t) = x (t) Jo + a (t) J

Kde Jo a J Sú to kolmé vektory jednotiek v pokynoch X a a respektíve. Grafu je pozorované, že vektorový modul r (t) Vždy v poriadku R, Polomer obvodu. Ak 9 je uhol, ktorý sa tvorí r S horizontálnou osou sa poloha tiež rovná:

r (t) = [RCOS θ(t)] Jo +[Rsen θ(t)] J

Uhol, ktorý sa tvorí r (T) S horizontálnou osou je centrálny uhol a jeho hodnota je:

9 = s/r

Kde s je obvodový oblúk a Rádio Rádio. Uhol θ Je to časová funkcia, takže môžete písať 9 = 9 (T), zavolať uhlová poloha.

Pretože rýchlosť je konštantná, častica opisuje rovnaké uhly v rovnakých časoch a v analógii s rovnomerným priamym pohybom, je napísaná:

9 = 9 (t) = θ_ani + Ωt

Tu θ_ani Je to počiatočný uhol meraný v radiánoch vzhľadom na referenčnú os, môže to byť 0 alebo akákoľvek hodnota a Ω je uhlová rýchlosť.

Uhlová rýchlosť a lineárna rýchlosť

Uhlová rýchlosť je prvá odvodená z uhlovej polohy a je označená ako co. Jeho hodnota je konštantná pre rovnomerný kruhový pohyb, pretože rovnaké uhly sú v rovnakých časoch oplotené. Inými slovami:

Uhlová rýchlosť prichádza v jednotkách radiánov. Pokiaľ ide o svoju časť, lineárna rýchlosť sa vypočíta podľa:

Lineárna rýchlosť je modul alebo veľkosť lineárnej rýchlosti, ktorá sa mení, keď sa častica otočí po jej trajektórii. Smer rýchlosti je teda tangenciálna adresa k obvodu.

Jednotky lineárnej rýchlosti v rovnomernom pohybe kruhového pohybu sú rovnaké ako pre lineárne pohyby: m/s (v medzinárodnom systéme SI), KM/H, CM/S a ďalšie.

Zrýchlenie

Na nasledujúcom obrázku je častica, ktorá sa pohybuje v harmonograme obvodu s konštantnou rýchlosťou. To znamená, že rýchlostný vektor má vždy rovnaký modul, ale mení smer, aby vyhovoval obvodu.

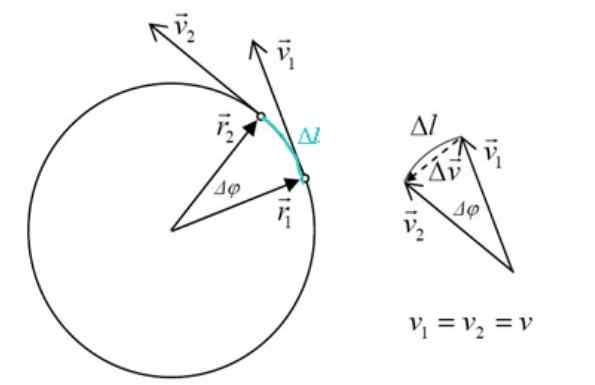Rýchlosť a zrýchlenie v rovnomernom pohybe kruhového. Zdroj: f. Zapata.

Akákoľvek zmena vo výsledkoch rýchlosti na zrýchlenie, ktoré podľa definície je:

Môže vám slúžiť: 31 typov sily vo fyzike a ich charakteristiky

Na obrázku vyššie je odčítanie medzi vektormi vložka₂ a vložka₁, ktorého výsledok je δvložka, vektor úmerný zrýchleniu. Ako vidíte, vždy poukazuje na stred obvodu, a preto sa nazýva centripetálne zrýchlenie alebo radiálne zrýchlenie.

Trojuholník tvorený vložka₂, vložka₁ a δvložka Je to podobné ako boksový trojuholník r₂, r₁ a δl, Byť Δgen v centrálnom uhle. Veľkosti r₂ a r₁ Sú rovnaké, takže:

r₂ = r₁ = r

Potom sú obe trojuholníky tieto vzťahy pre uhol:

Δφ = ΔR / r; Δφ = ΔV / v

Tučné písmo nie sú potrebné, pretože miera uhla závisí od veľkosti týchto vektorov. Vyrovnanie vyššie uvedených výrazov Z toho vyplýva, že:

 Tak:

Rozdelenie na obidvoch stranách AT, aby ste získali veľkosť zrýchlenia:

Ale ΔR / AT je veľkosť rýchlosti, ktorá sa nazýva vložka, preto:

Nakoniec zrýchlenie centripetálu je:

Obdobie a frekvencia

Pretože sa kruhový pohyb opakuje, je definované obdobie Tón rovnaké ako čas, ktorý trvá, kým sa mobil dokončí. Pretože dĺžka polomeru polomeru R je 2πr, uhol v radiánoch, keď sa otáčal, je 2π radiány a vyžaduje si čas t, uhlová rýchlosť je:

Ω = 2π / t

T = 2π / Ω

Obdobie jednotného pohybu kruhového pohybu sa meria v sekundách v medzinárodnom systéme.

Pokiaľ ide o svoju časť, frekvencia F Je to počet zákrut na jednotku času a je recipročným alebo inverzným obdobím:

F = n /t = 1 /t

Frekvenčná jednotka v medzinárodnom systéme je S^-1.

Jednotné príklady kruhového pohybu

Mnoho objektov sa otáča a vytvárajú rôzne účinky: kolesá, disky a turbíny. Po dosiahnutí prevádzkovej rýchlosti sa rotácia zvyčajne vykonáva konštantnou rýchlosťou. Kruhový pohyb je v každodennom živote taký bežný, že o tom takmer nikdy nepremýšľate, takže tu existujú nejaké blízke príklady, ktoré ho veľmi dobre ilustrujú:

Zemský pohyb

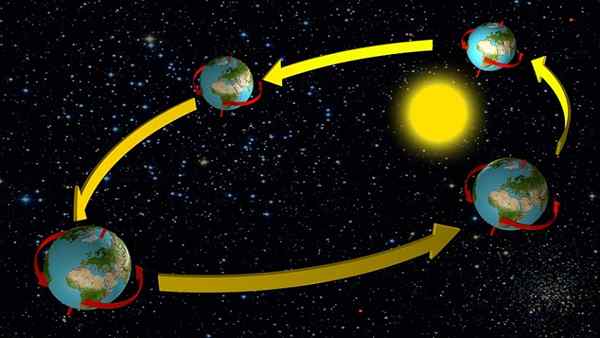
Zem a iné planéty slnečnej sústavy sa pohybujú v eliptických trajektóriách malej excentricity, s výnimkou ortuti, čo znamená, že v prvom prístupe sa dá predpokladať, že jeho pohyb je rovnomerný kruhový kruhový.

To má dobrú predstavu o rýchlosti prekladu okolo slnka, pretože v prípade Zeme je obdobie pohybu známe: jeden rok alebo 365 dní.

Častice na okraji albumu

Častice, ktoré sa točia na okraji starodávnych ropuchov alebo výstrelok ventilátora, sledujú rovnomerný kruhový pohyb, keď zariadenie dosiahne svoju reprodukčnú rýchlosť.

Môže vám slúžiť: Dirac Jordan Atomic Model: Charakteristiky a postuláty

Teleskop na hubble

Hubble Space Telescope sa točí okolo Zeme pri približne 7550 m/s.

Odstredivky

Práčky vykonávajú odstredený proces na stlačenie oblečenia, ktoré spočíva v rotácii vysokorýchlostného kontajnerového bubna. Sušičky sa tiež otáčajú na určitý čas s rovnomerným kruhovým pohybom.

Centrifugácia sa používa aj v laboratóriách napríklad na oddelenie zlúčenín, a tak oddeľuje svoje zložky podľa rozdielu v hustotách. Kedykoľvek sa hovorí o odstredení, existuje kruhový pohyb, ktorý je jednotný, aspoň na chvíľu.

Záhradné sprchy

Mnoho záhradných spŕch sa neustále otáča, aby pôda na vodu za pár.

Športový

Napríklad pri spustení kladiva, čo je olympijská disciplína, športovec otočí kovovú guľu s oceľovým káblom pripevneným k rukoväti. Cieľom je poslať loptu čo najviac, ale bez opustenia určitej oblasti.

Cvičenie

Častica sa pohybuje v kruhu s polomerom 2 m s konštantnou rýchlosťou v = 8 m/s, v opačnom smere ako hodiny. Spočiatku bola častice v r = +2 J m. Vypočítať:

a) uhlová rýchlosť Ω

b) jeho uhlová poloha 9 (t)

c) Obdobie pohybu

d) centripetálne zrýchlenie.

e) poloha častice po prechode t = π/4 s

Roztok

Z vzorca v = rΩ vyplýva, že:

Ω = v/r = (8 m/s)/2m = 4rad ∙ s^-1

Riešenie B

Keďže sa ako referenčná os na kladnú os x, častica je spočiatku pri 90 ° = π/2 radiány v súvislosti s uvedenou osou, pretože vyhlásenie hovorí, že počiatočná poloha je +2 J m, to znamená, že častica je v y = 2 m, keď pohyb začne nasledovať.

9 = 9 (t) = 9_ani + Ωt = π/2 + 4T

Riešenie c

T = 2π / Ω = 2π / 4 s = 0.5 π s

Riešenie d

a = v² / R = (8 m/ s)² / 2 m = 32 m/ s²

Riešenie e

θ (t) = π/2 + 4T → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radiány

To znamená, že po tomto čase je častica v polohe y = -2m J. Dáva to zmysel, pretože t = π/4 s je polovicou obdobia, preto častice prehliadli uhol 180 ° v anti -horskom zmysle od jeho počiatočnej polohy a musí mať pravdu v opačnej polohe.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Zapata, f. Kruhový pohyb. Získané z: Francesphysics.Blog.com.