Domovská stránka
Fyzický
Moment zotrvačných vzorcov, rovnice a príklady výpočtu

Fyzický

Moment zotrvačných vzorcov, rovnice a príklady výpočtu

2375
236
Alan Milota

On moment zotrvačnosti Z tuhého tela vzhľadom na určitú os rotácie predstavuje jeho odpor voči zmene jej uhlovej rýchlosti okolo tejto osi. Je úmerný hmotnosti a tiež k umiestneniu osi rotácie, pretože telo podľa jeho geometrie môže ľahšie otáčať okolo určitých osí ako v iných.

Predpokladajme rozsiahly objekt (pozostávajúci z mnohých častíc), ktorý sa môže otáčať okolo osi. Predpokladajme, že sily koná F, tangenciálne aplikované na hmotný prvok ΔM_Jo, ktorý vytvára krútiaci moment alebo moment, ktorý dal τ_slepo= ∑r_Jo X F_Jo. Vektor r_Jo Je to pozícia ΔM_Jo(Pozri obrázok 2).

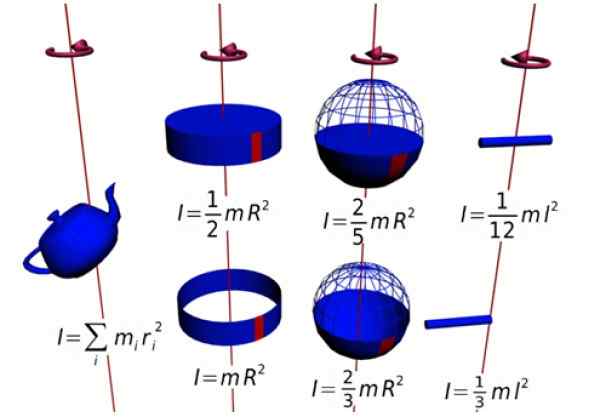
postava 1. Momenty zotrvačnosti niekoľkých postáv. Zdroj: Wikimedia Commons.

Tento okamih je kolmá na rotáciu (adresa +K = opustenie papiera). Pretože pevnosť a radiálna poloha sú vždy kolmé, krížový produkt zostáva:

τ_slepo = ∑ f_Jo r_Jo klimatizovať = ∑ (ΔM_Jodo_Jo) r_Joklimatizovať = ∑ ΔM_Jo(_Jo r_Jo) klimatizovať

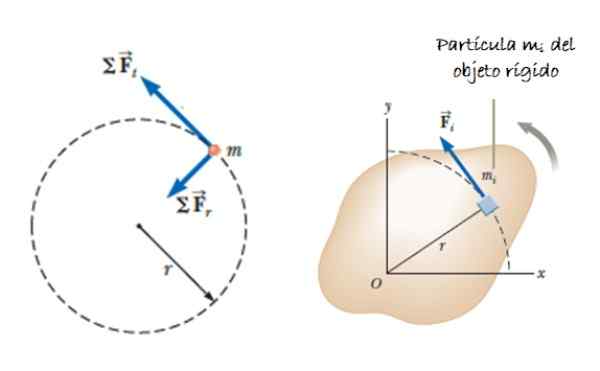Obrázok 2. Častica patriace k rotácii tuhej pevnej látky. Zdroj: Serway, r. 2018. Fyzika pre vedu a inžinierstvo. Zväzok 1. Učenie sa.

Zrýchlenie a_Jo predstavuje tangenciálnu zložku zrýchlenia, pretože radiálne zrýchlenie neprispieva k krútiacim momentom. V závislosti od uhlového zrýchlenia α môžeme uviesť, že:

do_Jo = α R_Jo

Preto je čistý krútiaci moment taký:

τ_slepo = ∑ ΔM_Jo(α R_Jo²) K = (∑ r_Jo² ΔM_Jo) α klimatizovať

Uhlové zrýchlenie a je rovnaké pre celý objekt, preto nie je ovplyvnený indexom „I“ a môže nechať súčet, čo je presne okamih zotrvačnosti symbolizovaného objektu pomocou písmena I:

I = ∑ r_Jo² ΔM_Jo

Toto je okamih zotrvačnosti diskrétneho hmotnostného rozdelenia. Ak je distribúcia nepretržitá, súčet sa nahradí integrálom a ΔM sa stáva masovým diferenciálom Dm. Integrál sa vyrába predovšetkým objekt:

I = ∫_M(r²) Dm

Jednotky okamihu zotrvačnosti v medzinárodnom systéme, ak sú kg x m². Je to skalárne a kladné množstvo, pretože je to produkt cesta podľa štvorca vzdialenosti.

[TOC]

Príklady výpočtu

Rozšírený objekt, ako napríklad tyč, disk, guľa alebo iný, ktorého hustota ρ Je konštantný a vie, že hustota je kvocient hmotnosti - objem, hmotný diferenciál Dm Je napísaný ako:

ρ = dm/dv → dm = ρDV

Nahradenie integrálu pre moment zotrvačnosti máme:

I = ∫r² ρdv = ρ ∫r²DV

Toto je všeobecný výraz, ktorý platí pre trojrozmerný objekt, ktorého objem Vložka a pozícia r Sú funkciami vesmírnych súradníc X, a a z. Všimnite si, že je konštantná, hustota je mimo integrálu.

Hustota ρ Je tiež známa ako objemová hustota, ale ak je objekt veľmi plochý, ako plech alebo veľmi tenký a úzky ako tyč, je možné použiť ďalšie formy hustoty, pozrime sa: Pozrime sa:

Môže vám slúžiť: pohyb rotácie zeme

- Pre veľmi jemný list je hustota, ktorá sa má použiť dávať je oblasť oblasti.

- A ak ide o tenkú tyč, kde je relevantná iba dĺžka, používa sa lineárna hmotnosť hustota λ a diferenciál dĺžky podľa osi použitej ako referencia.

V nasledujúcich príkladoch sa všetky objekty považujú za rigidné (neformovateľné) a majú rovnomernú hustotu.

Moment zotrvačnosti tenkej tyče vzhľadom na os, ktorá prechádza stredom

Tu sa chystáme vypočítať okamih zotrvačnosti tenkého, tuhého, homogénneho tyče, dĺžky L a hmotnosti m, vzhľadom na os, ktorá prechádza prostriedkami.

V prvom rade je potrebné zriadiť súradnicový systém a zostaviť postavu s primeranou geometriou, ako je táto:

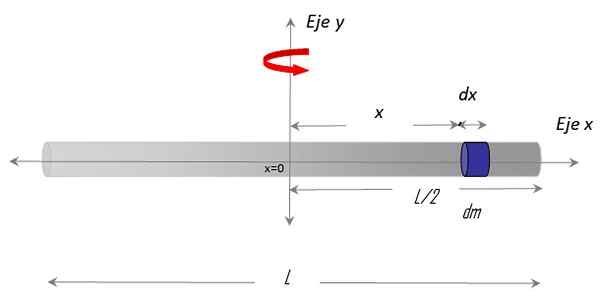Obrázok 3. Geometria na výpočet momentu zotrvačnosti tenkej tyče vzhľadom na vertikálnu os, ktorá prechádza jeho stredom. Zdroj: f. Zapata.

Bol vybraný X os x pozdĺž baru a Os y ako os rotácie. Postup na stanovenie integrálu si tiež vyžaduje výber hromadného diferenciálu na bare s názvom nazývaný Dm, ktorý má diferenciálnu dĺžku Dx a je umiestnený v polohe X svojvoľné, vzhľadom na centrum x = 0.

Podľa definície hustoty lineárnej hmotnosti λ:

λ = m/l

Ak je hustota rovnomerná, čo je platné pre M a L, je tiež pre DM a DX:

λ = dm/dx → dm = λdx.

Na druhej strane, hmotnostný prvok je v polohe X, Potom nahradením tejto geometrie v definícii máme definitívny integrál, ktorého limity sú extrémami tyče podľa súradníckeho systému:

$I=\int _Mr^2dm =\int_\frac-L2^\fracL2x^2\lambda dx=\lambda \left [\fracx^33 \right ]_\frac-L2^\fracL2=\frac\lambda 3\left [ \fracL^38-\left ( \frac-L^38 \right ) \right ]=\frac\lambda 12L^3$

Výmena lineárnej hustoty λ = m/l:

$I=\frac112ML^2$

Ak chcete nájsť okamih zotrvačnosti tyče vzhľadom na inú os rotácie, napríklad ten, ktorý prechádza jedným z jej koncov, môžete použiť Steinerovu vetu (pozri cvičenie vyriešené na konci) alebo vykonať priamy výpočet podobný tomu tu zobrazené tu, ale správne modifikujúce geometriu.

Moment zotrvačnosti albumu s ohľadom na os, ktorá prechádza jeho stredom

Veľmi tenký album, zúfalou hrúbkou je plochá postava. Ak je cesto rovnomerne rozložené v celej oblasti A, hustota hmoty σ je:

σ = M/a

Tak veľa Dm ako dávať zodpovedajú hmotnosti a ploche diferenciálneho kruhu zobrazeného na obrázku. Budeme predpokladať, že celá sada sa točí okolo osi a.

Môžete si predstaviť, že album je zložený, že mnoho rádiových sústredných prsteňov r, každý s príslušným momentom zotrvačnosti. Pridanie príspevkov všetkých krúžkov, až kým nedosiahnete rádio R, Budete mať celkovú zotrvačnosť albumu.

σ = dm/da → dm = σdávať

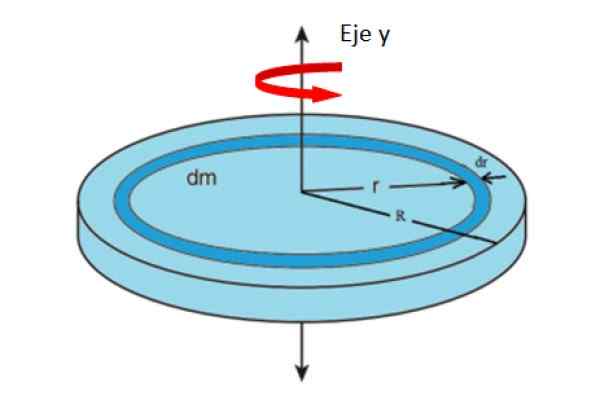Obrázok 4. Geometria na výpočet momentu zotrvačnosti albumu, vzhľadom na axiálnu os. Zdroj: f. Zapata.

Kde m predstavuje celé cesto albumu. Oblasť albumu závisí od jeho polomeru R ako:

Môže vám slúžiť: Rýchlosť šírenia vlny

A = π.r²

Odvodenie o R:

Da /dr = 2 = 2π.R → da = 2π.rdr

Nahradenie vyššie uvedeného v definícii i:

$I=\int _Mr^2dm=\int_0^Rr^2\left (\sigma dA \right )=\sigma \int_0^Rr^2\left (2\pi rdr \right )=2\pi \sigma \int_0^Rr^3dr$ Po vyhodnotení integrálnych výsledkov:

$I=2\pi \sigma \fracR^44$

Výmena σ = m/(π.R²) zostáva:

$I=2\pi \sigma \fracR^44=2\pi\left (\fracM\pi R^2 \right )\left (\fracR^44 \right )=\frac12MR^2$

Moment zotrvačnosti pevnej gule vzhľadom na priemer

Radius R Sphere možno považovať za sériu naskladaných diskov na sebe, kde každý album nekonečného masového albumu Dm, rozhlas r a hrúbka DZ, Má moment zotrvačnosti, ktorú dal:

dal_disk = (½) r²Dm

Na nájdenie tohto rozdielu bol vzorec predchádzajúcej sekcie jednoducho prijatý a nahradený M a R podľa Dm a r, respektíve. Takýto album je možné vidieť v geometrii na obrázku 5.

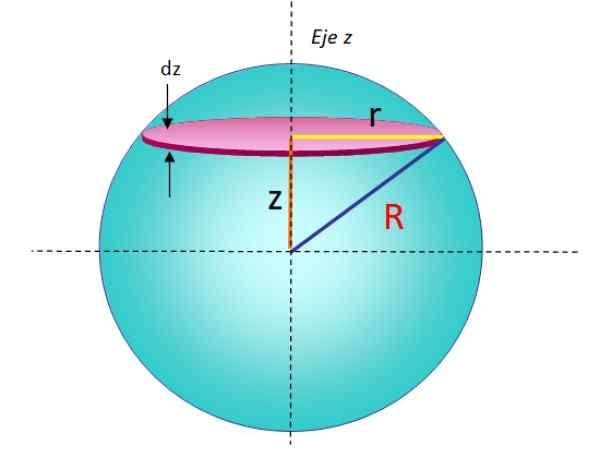Obrázok 5. Geometria na výpočet momentu zotrvačnosti guľovej gule s polomerom vzhľadom na os, ktorá prechádza priemerom. Zdroj: f. Zapata.

Pridaním všetkých momentov infinitesimálnej zotrvačnosti naskladaných diskov sa získa moment celkovej zotrvačnosti gule:

Jo_sféra = ∫di_disk

Čo je rovnocenné:

I = ∫_sféra(½) r²Dm

Ak chcete vyriešiť integrál, musíte vyjadriť Dm správne. Ako vždy sa dosahuje z hustoty:

ρ = m/v = dm/dv → dm = ρ.DV

Objem diferenciálneho disku je:

DV = základná plocha x výška

Výška albumu je hrúbka DZ, zatiaľ čo základná oblasť je πr², preto:

Dv = πr²DZ

A nahradenie integrovaného by bolo takéto:

I = ∫_sféra(½) r²Dm = ∫ (½) r²(ρπr²Dz)

Ale pred integráciou musí byť. Prostredníctvom vety Pythagory:

R² = r² + z² → R² = R² - z²

To nás vedie k:

I = ∫_sféra(½) ρ r²(πr²dz) = ∫_sféra(½) ρ π r⁴DZ= ∫_sféra(½) ρ π (r² - z²)² DZ

Na integráciu celej sféry si všimneme, že Z sa mení medzi -R a R, preto:

$I=\frac12\pi \rho \left [\int_-R^RR^4dz-\int_-R^R2R^2z^2dz+\int_-R^Rz^4dz \right ]$
$I=\frac12\pi \rho \left [R^4z-2R^2\left (\fracz^33 \right )+\fracz^55 \right ]_-R^R=\frac815\pi \rho R^^5$

S vedomím, že ρ = m/v = m/[(4/3) πr³] Nakoniec sa získa po zjednodušení:

$I=\frac815\pi \left (\fracM\frac43\pi R^3 \right )R^5=\frac25MR^2$

Moment zotrvačnosti tuhého valca vzhľadom na axiálnu os

Pre tento objekt sa používa metóda podobná metóde používanej pre guľu, iba tentoraz je jednoduchšie, ak je valec predstavený pre pultové valcovité škrupiny r, hrúbka DR a výška H, Akoby boli vrstvami cibule.

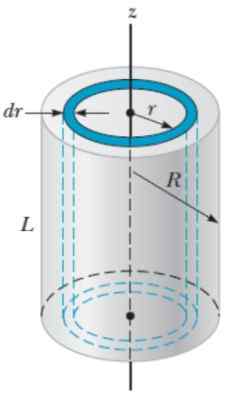Obrázok 6. Geometria na výpočet momentu zotrvačnosti tuhého polomeru valca R s rešpektom k axiálnej osi. Zdroj: Serway, r. 2018. Fyzika pre vedu a inžinierstvo. Zväzok 1. Cengage.

Hlasitosť DV valcovej vrstvy je:

DV = 2π.Rl.DR

Preto je hmotnosť Cascaron:

Môže vám slúžiť: mikroskopická stupnica: vlastnosti, počítanie častíc, príklady

Dm = ρ.Dv = ρ. 2π.r.L.DR

Tento výraz sa nahradí v definícii momentu zotrvačnosti:

$I=\int _Mr^2dm = \int_0^Rr^22\pi \rho Lrdr=2\pi \rho L\int_0^Rr^3dr=2\pi \rho L\left (\fracR^44 \right )$ Vzhľadom na to ρ = m / (π.R²L) Zostane:

$I=2\pi \left (\fracM\pi R^2L \right ) L\left (\fracR^44 \right )=\frac12MR^2$

Predchádzajúca rovnica naznačuje, že moment zotrvačnosti valca nezávisí od jej dĺžky, ale iba od jej hmoty a iba polomeru. Jo L zmenený, okamih zotrvačnosti vzhľadom na axiálnu os bude naďalej rovnaký. Pre tento dôvod, Jo valca sa zhoduje s valcom predtým vypočítaného tenkého albumu.

Moment zotrvačnosti obdĺžnikového plechu vzhľadom na os, ktorá prechádza cez jeho stred

Ten Os y Vodorovná ako os otáčania. Obrázok nižšie zobrazuje potrebnú geometriu na vykonanie integrácie:

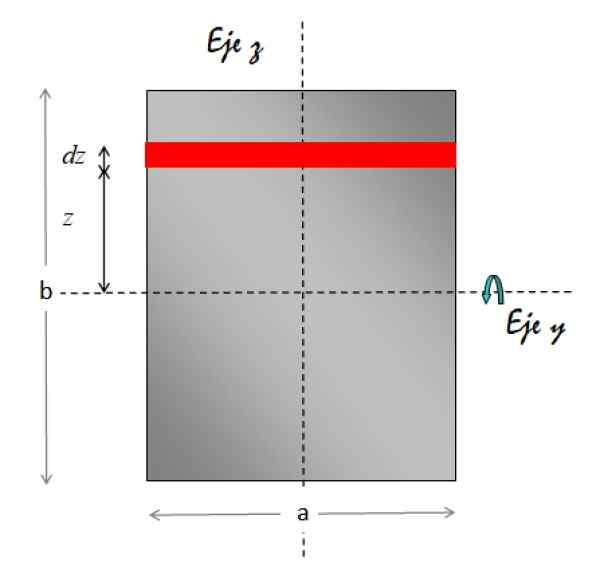Obrázok 7. Geometria pre výpočet momentu zotrvačnosti obdĺžnikovej doštičky vzhľadom na rovnobežnú os k hárku a ktorá prechádza cez jeho stred. Zdroj: f. Zapata.

Prvok oblasti označený červenou farbou je obdĺžnikový. Jeho oblasť je preto základná x výška:

da = a.DZ

Preto je hmotnostný diferenciál:

Dm = σ.da = σ.(.Dz)

Pokiaľ ide o vzdialenosť prvku oblasti k osi rotácie, vždy je to z. To všetko nahradíme v integráli momentu zotrvačnosti:

$I=\int _Mz^2dm=\int_\frac-b2^\fracb2z^2\left (\sigma adz \right )=\sigma a\int_\frac-b2^\fracb2z^2dz=\sigma a\left [ \fracz^33 \right ]_\frac-b2^\fracb2=\frac112\sigma ab^3$

Teraz je hustota povrchovej hmoty σ nahradená:

σ = m/ab

A určite je to takto:

$I=\frac112\sigma ab^3=\frac112\left ( \fracMab \right )ab^3=\frac112Mb^2$

Všimnite si, že je to ako tenký pruh.

Moment zotrvačnosti štvorcového plechu vzhľadom na os, ktorá prechádza cez jeho stred

Na štvorec na boku L, V predchádzajúcom výraze platí pre obdĺžnik, hodnota b pri jednom L:

$I=\frac112ML^2$

Vety momentu zotrvačnosti

Existujú dve obzvlášť užitočné vety na zjednodušenie výpočtu momentov zotrvačnosti vzhľadom na iné osi, čo by inak mohlo byť komplikované, aby sa zistilo pre nedostatok symetrie. Tieto vety sú:

Steinerova veta

Tiež nazývaný veta paralelnej osi, sa týka momentu zotrvačnosti týkajúcej sa osi s inou, ktorá prechádza stredom hmotnosti objektu, pokiaľ sú osi rovnobežné. Aby sa to aplikuje, musí byť známa vzdialenosť D medzi týmito dvoma osami a samozrejme hmotnosťou M objektu.

Byť Jo_zmoment zotrvačnosti rozšíreného objektu vzhľadom na Z, ja osi_CmMoment zotrvačnosti vzhľadom na os, ktorá prechádza cez masové centrum uvedeného objektu, potom sa splní:

Jo_z = I_Cm + Md²

Alebo v zápise nasledujúceho obrázku: Jo_{z '} = I_z + Md²

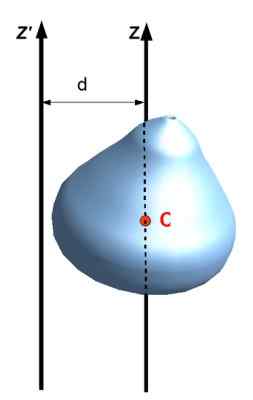Obrázok 8. Steinerova veta alebo paralelné osi. Zdroj: Wikimedia Commons. Jack pozri [CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Veta kolmej osi

Táto veta sa vzťahuje na ploché povrchy a hovorí: Moment zotrvačnosti plochého objektu okolo osi kolmej na ňu je súčet momentov zotrvačnosti okolo dvoch osí kolmých na prvú os:

Jo_z = I_X + Jo_a

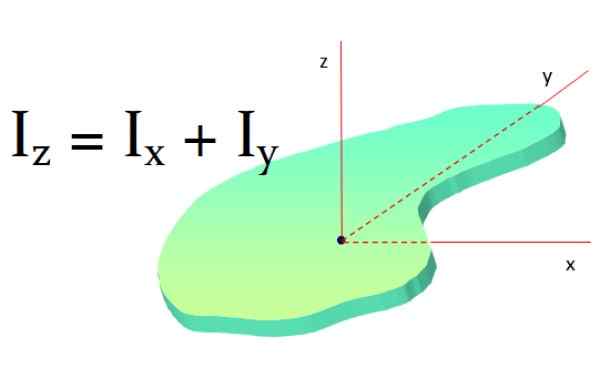Obrázok 9. Veta kolmej osi. Zdroj: f. Zapata.

Ak má objekt symetriu tak, že Jo_X a Jo_a Sú rovnaké, potom je splnené, že:

Jo_z = 2i_X

Cvičenie

Nájdite okamih zotrvačnosti tyče vzhľadom na os, ktorá prechádza jedným z jej koncov, ako je ten, ktorý je znázornený na obrázku 1 (nižšie a doprava) a na obrázku 10.

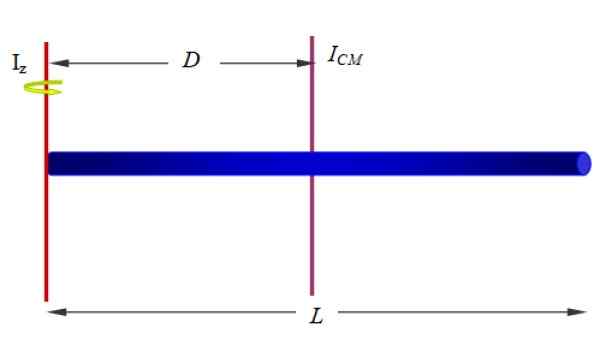Obrázok 10. Moment zotrvačnosti homogénnej tyče okolo osi, ktorá prechádza cez jeden koniec. Zdroj: f. Zapata.

Riešenie:

Už máme okamih zotrvačnosti baru okolo osi, ktorá prechádza cez geometrické centrum. Pretože bar je homogénny, v tom okamihu je jeho centrum hmoty, takže to bude naše Jo_Cm Aplikovať Steinerovu vetu.

Ak je dĺžka tyče L, Os Z je vo vzdialenosti d = l/2, preto:

Jo_z = I_Cm + Md²= (1/12) ml²+M (l/2)²= (1/3) ml²

Odkazy

Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 313-340
Rex, a. 2011. Základy fyziky. Pearson. 190-200.
Veta paralelnej osi. Obnovené z: hyperfyziky.Fytrický.Gsu.Edu.
Serway, r. 2018. Fyzika pre vedu a inžinierstvo. Zväzok 1. Cengage.
Univerzita. Moment zotrvačnosti sférických tuhých látok. Získané z: Laplace.my.je.
Univerzita. Moment zotrvačnosti systému častíc. Získané z: Laplace.my.je.
Wikipedia. Veta paralelnej osi. Zdroj: In.Wikipedia.orgán