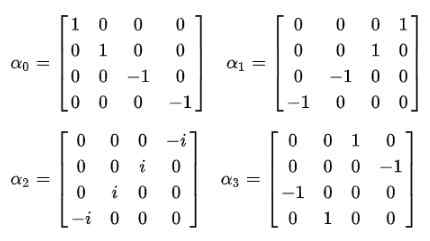
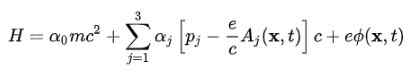Aomický model charakteristík Dirac Jordan a postulátov

On Atómový model Dirac-Jordan Je to relativistická zovšeobecnenie hamiltonovského operátora v rovnici, ktorá opisuje funkciu kvantovej vlny. Na rozdiel od predchádzajúceho modelu Schrodinger's, nie je potrebné ukladať točenie prostredníctvom princípu Pauliho vylúčenia, pretože sa zdá prirodzene.

Okrem toho model Dirac-Jordan obsahuje relativistické korekcie, interakciu spin-orgán a Darwinov termín, ktoré zodpovedajú za jemnú štruktúru elektronických hladín atómu.

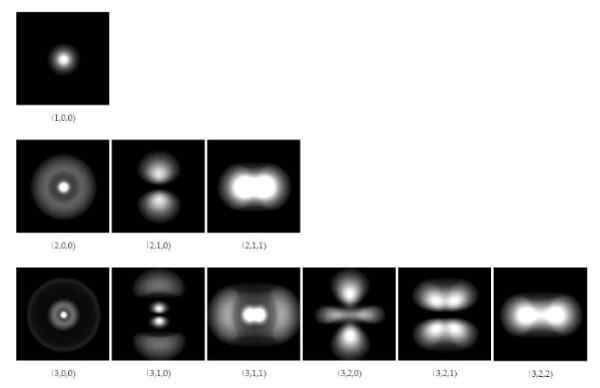
postava 1. Elektronické orbitály v atóme vodíka pre prvé tri hladiny energie. Zdroj: Wikimedia Commons.

Od roku 1928 vedci Paul a. M. Dirac (1902-1984) a Pascual Jordan (1902-1980) boli navrhnuté na zovšeobecnenie kvantovej mechaniky vyvinutej Schrodingerom, aby zahŕňali opravy Einsteinovej osobitnej relativity.

Dirac časť Schrodingerovej rovnice, ktorá pozostáva z diferenciálneho operátora, nazývaného Hamiltonian, ktorý funguje na funkcii známej ako Funkcia elektrónovej vlny. Schrodinger však nezohľadnil relativistické účinky.

Roztoky funkcií vlny umožňujú vypočítať oblasti, v ktorých sa elektrón okolo jadra nachádza s určitým stupňom pravdepodobnosti. Tieto regióny alebo oblasti sa nazývajú Orbitáli A závisia od určitých diskrétnych kvantových čísel, ktoré definujú energiu a uhlovú hybnosť elektrónu. 

[TOC]

Postuláty

V kvantových mechanických teóriách, či už relativistické alebo nie, neexistuje koncept dráh, pretože poloha ani rýchlosť elektrónu nie je možné špecifikovať súčasne. A navyše, špecifikácia jednej z premenných vedie k úplnému nepresnosti v druhej.

Pokiaľ ide o svoju časť, Hamiltonian je matematický operátor, ktorý pôsobí na funkciu kvantovej vlny a je postavený z elektrónovej energie. Napríklad voľný elektrón má celkovú energiu a to závisí od jeho lineárnej hybnosti p teda:

E = (p²)/ 2 m

Na vybudovanie Hamiltoniána začína z tohto výrazu a je nahradený p Kvantovým operátorom pre hybnosť: 

p = -I ħ ∂ /∂r 

Je dôležité poznamenať, že podmienky p a p Sú odlišné, pretože prvé je dynamika a druhá je Diferenciálny operátor spojené s hybnosťou. 

Môže vám slúžiť: atómový model leukipo: postuláty, obmedzenia, dôležitosť

Okrem toho je i imaginárna jednotka a ħ ħ Planck Constant vydelená 2π, týmto spôsobom sa získa Hamiltonovský operátor H voľného elektrónu:

H = (ħ²/2m) ∂² /∂r² 

Ak chcete nájsť Hamiltoniana elektrónu v atóme, pridá sa elektrónová interakcia s jadrom: 

H = (ħ2/2M) ∂² /∂r²  - Eφ (r)

V predchádzajúcom výraze -e je elektrónový elektrický náboj a φ (r) elektrostatický potenciál produkovaný centrálnym jadrom.

Teraz operátor H pôsobí na vlnovú funkciu ψ podľa Schrodingerovho rovnice, ktorá je napísaná takto:

H ψ = (i ħ ∂ /∂t) ψ

Štyri postuláty Dirac

Prvé postuláty: Relativistická vlnová rovnica má rovnakú štruktúru ako Schrodingerova vlnová rovnica, aké zmeny je H:

H ψ = (i ħ ∂ /∂t) ψ

Druhý postulát: Hamiltonov operátor je postavený na základe Einsteinovho vzťahu medzi energetickými momentum, ktorý je napísaný takto:

E = (m² c⁴ + p² c²)^1/2

V predchádzajúcom vzťahu, ak má častica hybnosť p = 0, potom máte slávnu rovnicu E = MC² ktorá súvisí s pokojovou energiou akejkoľvek hmotnosti m rýchlosťou svetla C.

Tretí postulát: Na získanie hamiltonovského operátora sa používa rovnaké pravidlo kvantizácie použité v Schrodingerovej rovnici:

p = -I ħ ∂ /∂r

Na začiatku nebolo jasné, ako zvládnuť tento diferenciálny operátor pôsobiaci v odmocninovom koreni, takže Dirac sa vydal na získanie lineárneho hamiltonovského operátora v operátorovi hybnosti a odtiaľ sa objavil jeho štvrtý postulát.

Miestnosť: Aby sa zbavil druhého koreňa v relativistickej energetickej vzorci, Dirac navrhol pre e nasledujúcu štruktúru²:

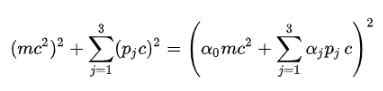
Samozrejme je potrebné určiť alfa koeficienty (a0, a1, a2, a3), aby sa to splnilo.

Diracova rovnica

Rovnica Dirac bola prvýkrát zdvihnutá pre voľný elektrón pomocou štruktúry navrhnutej vo štvrtom postuláte. Zostáva to nasledovne: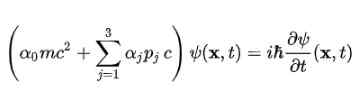

Môže vám slúžiť: Počuť silu: povrchové a hmotnostné sily

Vo svojej kompaktnej podobe sa rovnica Dirac považuje za jednu z najkrajších matematických rovníc na svete:

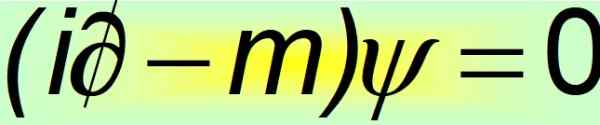Obrázok 2. Diracova rovnica kompaktná. Zdroj: f. Zapata.

A to je vtedy, keď sa preukáže, že konštantné Alfas nemôžu byť skalárnymi množstvami. Jediným spôsobom, ako je splnená rovnosť štvrtého postulátu, je to, že ide o konštantné matice 4 × 4, ktoré sú známe ako Matice Dirac:

Okamžite sa pozoruje, že vlnová funkcia prestane byť skalárnou funkciou a stáva sa štvorpohodovým vektorom Zverenie:

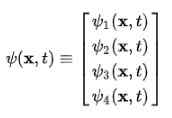
Atóm Dirac-Jordan

Na získanie atómového modelu je potrebné presunúť sa z voľnej elektrónovej rovnice na elektrón v elektromagnetickom poli produkovanom atómovým jadrom. Táto interakcia sa berie do úvahy začlenením potenciálneho skalárneho φ a potenciálneho vektora Do V Hamiltoniáne:

Funkcia vlny (ESPINOR), ktorá je výsledkom začlenenia tohto Hamiltoniána, má nasledujúce vlastnosti: 

- Spĺňa špeciálnu relativitu, pretože zohľadňuje vnútornú energiu elektrónu (prvé funkčné obdobie relativistického Hamiltoniana)

- Má štyri riešenia zodpovedajúce štyrom zložkám Espinor

- Prvé dve roztoky zodpovedajú jednému, ktoré sa točia +½ a druhé k rotácii - ½ 

- Nakoniec ďalšie dve riešenia predpovedajú existenciu antihmoteru, pretože zodpovedajú existencii pozitrónov protikladov protikladných protikladov.

Veľkou výhodou rovnice Dirac je to, že základné hamiltonské korekcie Schrodinger H (o) sa môžu rozdeliť na niekoľko výrazov, ktoré ukážeme nižšie:

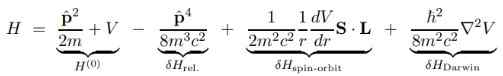
V predchádzajúcom výraze V je potenciálne skalárne, pretože potenciálny vektor Do Je neplatný, ak má centrálny stacionárny protón, a preto sa neobjaví.

Dôvod, prečo sú Diracove korekcie týkajúce sa Schrodingerových riešení vo vlnovej funkcii. Vyplývajú zo skutočnosti, že posledné tri obdobia opraveného Hamiltoniána sú rozdelené rýchlosťou C na námestí, obrovským číslom, vďaka ktorému sú tieto výrazy číselne malé.

Môže vám slúžiť: Vy Canis Majoris: Objav, charakteristiky, štruktúra, školenie a vývoj

Relativistické korekcie energetického spektra

Pomocou rovnice DIC-Jordan sa nachádzajú korekcie do spektra elektrónovej energie v atóme vodíka. Existujú tiež korekcie energie v atómoch s viac ako jedným elektrónom približne prostredníctvom metodológie známeho ako teória porúch.

Podobne model Dirac vám umožňuje nájsť korekciu jemnej štruktúry na hladinách energie vodíka. 

Avšak ešte jemnejšie korekcie, ako je štruktúra hyperfínu a jahňací posun, sa získavajú z pokročilejších modelov, ako sú napríklad Kvantová teória Campos, Narodený presne v dôsledku príspevkov modelu Dirac.

Nasledujúci obrázok ukazuje, ako sú Diracove relativistické korekcie na úrovni energie:

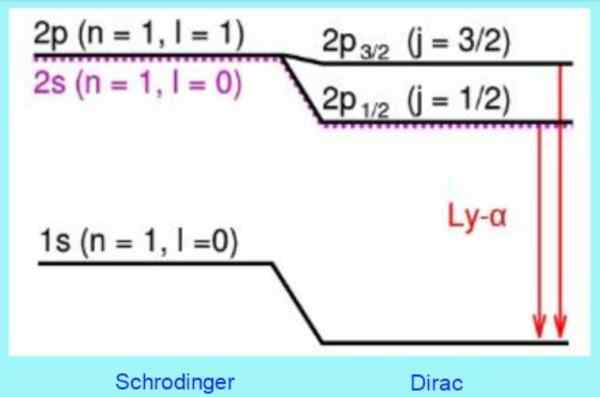Obrázok 3. Korekcie modelu Dirac na hladinách atómu vodíka. Zdroj: Wikimedia Commons.

Napríklad riešenia rovnice Dirac správne predpovedajú posun pozorovaný na úrovni 2S. Je to dobre známa korekcia jemnej štruktúry v línii Lyman - Alfa vodíkového spektra (pozri obrázok 3).

Mimochodom, jemná štruktúra je názov, ktorý prijíma v atómovej fyzike rozvíjanie riadkov emisného spektra atómov, čo je priamym dôsledkom elektronického rotácie.

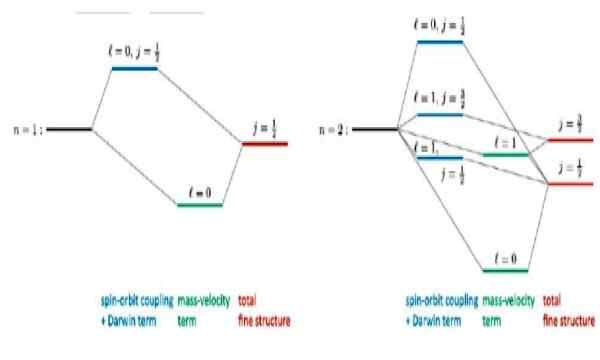Obrázok 4. Jemná štruktúra, ktorá sa rozvíja pre základný stav n = 1 a prvý excitovaný stav n = 2 v atóme vodíka. Zdroj: R Wirnata. Relativistické korekcie atómov podobných vodíkom. Výskumy.slepo

Predmety záujmu

Broglie atómový model.

Atómový model Chadwick.

Heisenberg atómový model.

Perrin atómový model.

Thomson Atomic Model.

Atómový model Dalton.

Schrödinger atómový model.

Atómový model demokritu.

Leucipo atómový model.

Bohr atómový model.

Súčasný atómový model.

Odkazy

1. Atómová teória. Zotavené z Wikipédie.orgán.
2. Elektrónový magnetický moment. Zotavené z Wikipédie.orgán.
3. Quanta: Príručka konceptov. (1974). Oxford University Press. Zotavené z Wikipédie.orgán.
4. Atómový model Dirac Jordan. Zotavené z Prezi.com.
5. Nový kvantový vesmír. Cambridge University Press. Zotavené z Wikipédie.orgán.