Približné meranie amorfných obrázkov príklad a cvičenie

Ten Približné meranie Z amorfných figúr pozostáva zo série metód používaných na určenie oblasti alebo obvodu geometrických figúr, ktoré nie sú trojuholníky, štvorce, kruhy atď. Niektoré sú rozšíriteľné na tri rozmerové čísla.

V podstate meranie spočíva v pravidelnom vytváraní sietí, ako sú obdĺžniky, štvorce alebo lichobežníky, ktoré pokrývajú približne povrch. Presnosť prístupu oblasti získanej týmito metódami sa zvyšuje s jemnosťou alebo hustotou sietí.

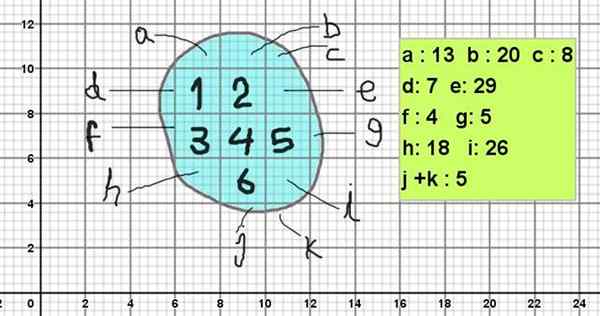
postava 1. Kamene v tvare amorfných figúr. Zdroj: pxfuel.

Obrázky 1 a 2 ukazujú rôzne amorfné postavy. Na výpočet oblasti je sietí zložené z 2 x 2 štvorcov, ktoré sú zase rozdelené na dvadsať -Five štvorce 2/5 x 2/5.

Pridanie oblastí hlavných štvorcov a sekundárnych štvorcov sa získa približná plocha amorfnej postavy.

Obrázok 2. Retikulovanie na výpočet plochy jednej z amorfných figúr približným spôsobom. Zdroj: f. Zapata

[TOC]

Oblasť pod krivkou

Často je potrebné vypočítať oblasť pod krivkou medzi dvoma limitnými hodnotami. V tomto prípade je možné namiesto štvorcového subserku obdĺžnikové pruhy vysledovať približne v oblasti pod uvedenou krivkou.

Súčet všetkých obdĺžnikových pruhov sa nazýva Riemannova suma alebo suma. Obrázok 3 zobrazuje oddiel intervalu [a, b], na ktorom chcete určiť približne oblasť pod krivkou.

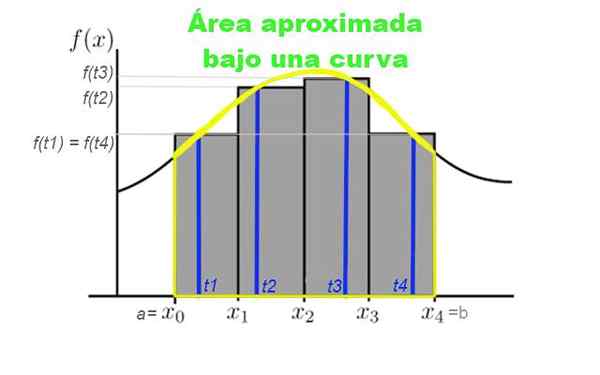Obrázok 3. Rozdelenie intervalu [a, b] v štyroch subintervaloch, ktoré sa zvyčajne berú z rovnakej šírky. Výška obdĺžnikov je určená hodnotou krivky pre TK patriace k subintervolám. Zdroj: f. Zapata.

Predpokladajme, že chcete vypočítať oblasť pod krivkou danou funkciou y = f (x), kde x patrí do intervalu [a, b], v rámci ktorého chcete vypočítať oblasť. Z tohto dôvodu sa vytvorí oddiel N prvkov v tomto intervale:

Môže vám slúžiť: 60 deliteľov

Oddiel = x0 = a, x1, x2, ..., xn = b.

Potom sa približná oblasť pod krivkou daná y = f (x) v intervale [a, b] sa dosiahne nasledujúcou sumou:

S = ∑_{K = 1}ⁿ f (t_{klimatizovať}) (X_{klimatizovať} - X_K-1)

Kde t_{klimatizovať} je medzi x_K-1 a x_{klimatizovať}: X_K-1 ≤ t_{klimatizovať} ≤ x_{klimatizovať} .

Obrázok 3 zobrazuje súčet Riemanna krivky y = f (x) v intervale [x0, x4]. V tomto prípade sa vytvorilo rozdelenie štyroch subintervalov a súčet predstavuje celkovú plochu šedých obdĺžnikov. 

Táto suma predstavuje prístup k oblasti pod krivkou F medzi Abscissas x = x0 a x = x4.

Prístup k oblasti pod krivkou sa zlepšuje v rozsahu, v akom je číslo n Oddiel je väčší a má tendenciu byť presne oblasť pod krivkou, keď číslo n oddiely majú tendenciu nekonečno. 

V prípade, že krivka je reprezentovaná analytickou funkciou, hodnoty f (t_{klimatizovať}) Sa vypočítavajú hodnotenie uvedenej funkcie v hodnotách t_{klimatizovať}. Ak však krivka nemá analytický výraz, zostanú nasledujúce možnosti:

1. Priblížte sa k krivke funkciou, napríklad polynóm.
2. Vezmite karteziánske súradnice bodov, kde je krivka zachytená s čiarami x = t_{klimatizovať}.

Pravidelné intervaly

V závislosti od výberu hodnoty TK v intervale [x_{klimatizovať}, X_K-1], suma môže preceňovať alebo podceňovať presnú hodnotu oblasti pod krivkou funkcie y = f (x). Najvýhodnejšou vecou je zaujať bod TK, v ktorom je chýbajúca oblasť približne rovnaká ako zostávajúca oblasť, hoci nie vždy je možné urobiť takúto voľbu.  

Môže vám slúžiť: Multiplikatívna inverzia: Vysvetlenie, príklady, vyriešené cvičenia

Vezmite TK na konci

Najpraktickejšou vecou je potom používať pravidelné intervaly širokého δx = (b - a)/n, kde a a b sú minimálne a maximálne hodnoty Abscissa, zatiaľ čo n je počet pododdielov.

V takom prípade sa oblasť pod krivkou blíži:

Oblasť = f (a+Δx)+f (a+2Ax)+…+f [a+(n-1] Δx+f (b)*Δx

V predchádzajúcom výraze bol TK odobratý na pravom konci subintervalu.

Vezmite TK na ľavom konci

Ďalšou praktickou možnosťou je vziať hodnotu TK na ľavom konci, v takom prípade súčet, ktorý sa približuje, je vyjadrená ako:

Plocha = [f (a)+f (a+δx)+…+f (a+(n-1) δx)*δx

TK ako centrálna hodnota

V prípade, že je TK vybraná ako centrálna hodnota pravidelného subintervalu šírky AX, súčet, ktorý sa približuje ploche pod krivkou, je:

Oblasť = [f (a+Δx/2)+f (a+3Ax/2)+…+f (b- Δx/2)]*Δx

Ktorýkoľvek z týchto výrazov má tendenciu presnú hodnotu v rozsahu, v akom je počet subdivízií svojvoľne veľký, to znamená, že AX má sklon k nule, ale v tomto prípade je počet podmienok sumy nesmierne veľký s následnými výpočtovými nákladmi. 

Príklad

Obrázok 2 zobrazuje amorfnú postavu, ktorej obrys je podobný kamene obrazu 1. Na výpočet svojej plochy sa umiestni na sieťovinu s hlavnými štvorcami 2 x 2 jednotiek na štvorec (napríklad môžu byť 2 cm²).

A keďže každé štvorce je rozdelené do 5 x 5 pododdielov, potom má každá podoblasť plochu 0,4 x 0,4 štvorcových jednotiek (0,16 cm²).

Obrázok na obrázku by sa vypočítal nasledovne:

Môže vám slúžiť: spoločná faktorizácia: príklady a cvičenia

Oblasť = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

To znamená:

Oblasť = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Cvičenie

Vypočítajte približne plochu pod krivkou danou funkciou f (x) = x² Stávka A = -2 až B = +2. Aby ste to dosiahli, napíšte sumu pre N Pravidelné oddiely intervalu [a, b] a potom preberte matematický limit pre prípad, že počet oddielov má tendenciu nekonečno. 

Riešenie

Po prvé, interval oddielu je definovaný ako 

Δx = (b - a)/n. 

Potom je suma pre právo zodpovedajúce funkcii f (x) ako je táto:

A = -2 a b =+2 sa nahradia tak, aby interval alebo krok boli Δx = 4/n. V tomto prípade súčet pre funkciu f (x) = x² je:

 Vyvinie sa binomický štvorcový binomický: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Jo²

A potom sa nahradí v súde:

Oddelenie súčtov a získanie konštantných množstiev ako spoločného faktora každej sumy sa získa:

 Prvá z suma, druhá je:

A tretí je:

Výmena vyjadrenia súčtu, ktorú máte:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Pri výbere veľkej hodnoty pre n máte dobrý prístup k oblasti pod krivkou. V tomto prípade je však možné dosiahnuť presnú hodnotu, ktorá má matematický limit, keď N má tendenciu nekonečno:

Oblasť = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Oblasť = 16 - (64/2)+ (64/3) = 16/3 = 5,333.

Odkazy

1. Casteleiro, J. M. 2002. Komplexný výpočet (ilustrované vydanie). Madrid: ESIC Editorial.
2. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
3. Purcell, e. 2007. Výpočet analytickou geometriou. 9NA. Vydanie. Pearson Vzdelanie.
4. Jednoznačný. História koncepcie integrálu. Získané z: úložiska.Jednoznačný.je
5. Uis. Sumy Riemann. Obnovené z: matematiky.Uis.Edu.co
6. Wikipedia. Oblasť. Obnovené z: je.Wikipedia.com