Matematika

Vážený priemer, ako sa vypočíta, príklady a cvičenia

Vážený priemer, ako sa vypočíta, príklady a cvičenia

Ten Vážený priemer alebo vážený aritmetický priemer, je to centrálna miera tendencie, v ktorej pre každú hodnotu xJo ktoré môžu mať premennú x, priradí peso pJo. Výsledkom je označením váženého priemeru xp, Máš:

Pri zhrnutí súčtu je vzorec váženého priemeru:

Kde n predstavuje množstvo hodnôt vybraných z premennej x.

PJo, čo sa tiež nazýva váh, Je to miera dôležitosti, ktorú výskumný pracovník pripisuje každej hodnote. Tento faktor je svojvoľný a vždy pozitívny.

V tomto váženom priemere sa líši od jednoduchého aritmetického priemeru, pretože v tomto je každá z hodnôt xn Má rovnaký význam. V mnohých aplikáciách však výskumný pracovník možno domnieva, že niektoré hodnoty sú dôležitejšie ako iné a pridelí váhu podľa svojich kritérií.

Tu je najznámejší príklad: Predpokladajme, že študent predstavuje hodnoty v jednom predmete a všetky majú rovnakú váhu v záverečnej poznámke. V tomto prípade na výpočet konečnej poznámky bude stačiť na to, aby sa vytvoril jednoduchý priemer, to znamená, pridať všetky kvalifikácie a vydeliť výsledok n.

Ale ak má každá aktivita inú váhu, pretože niektorí vyhodnotia dôležitejší alebo zložitejší obsah, potom bude potrebné vynásobiť každé hodnotenie podľa ich príslušnej hmotnosti a potom pridať výsledky, aby ste získali konečné hodnotenie. Uvidíme, ako vykonať tento postup v sekcii vyriešených cvičení.

[TOC]

Príklady

postava 1. Vážený priemer sa uplatňuje pri výpočte indexu spotrebiteľských cien, indikátora inflácie. Zdroj: pxhere.

Príklad vyššie opísaných kvalifikácií je jedným z najtypickejších z hľadiska uplatňovania váženého priemeru. Ďalšou veľmi dôležitou aplikáciou v ekonómii je Index spotrebiteľských cien ani Index cien spotrebiteľa IPC, tiež nazývaný rodinný kôš a to slúži ako hodnotiteľ inflácie v ekonomike.

Môže vám slúžiť: uhly a trojuholníky

Vo svojom vypracovaní sa berie do úvahy séria položiek, ako sú potraviny a nealkoholické nápoje, oblečenie a obuv, lieky, preprava, komunikácia, vzdelávanie, voľný čas a iné tovary a služby.

Odborníci prideľujú každému poľu váhový faktor, podľa ich dôležitosti v živote ľudí. Ceny sa zhromažďujú na stanovenú dobu a so všetkými informáciami, ktoré sa vypočíta IPC uvedeného obdobia.

Hmotnostné centrum systému častíc

Vo fyzike má vážený priemer dôležitú aplikáciu, ktorá sa má vypočítať Mass Center systému častíc. Tento koncept je veľmi užitočný pri práci s rozšíreným telom, v ktorom by sa mala zohľadniť jeho geometria.

Hmotnostné centrum je definované ako bod, v ktorom sa koncentruje celá hmotnosť rozšíreného objektu. V tomto bode sa sily môžu aplikovať napríklad ako hmotnosť, a tak vysvetliť ich pohyby prekladu a rotácie, prostredníctvom rovnakých techník, s ktorými pracovali, keď mali byť všetky objekty časticami.

Jednoducho sa začína predpokladať, že rozšírené telo sa skladá zo množstva N častíc, z ktorých každá z nich s hmotnosťou m a jeho vlastná poloha vo vesmíre: súradnicový bod (XJo, aJo, zJo).

Byť XCm Súradnica X Z CM Downtown, potom:

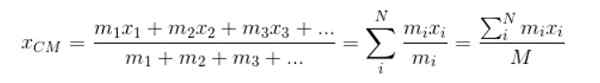
M predstavuje celkovú hmotnosť systému. Pokračuje rovnakým spôsobom na nájdenie súradníc aCm a zCm:

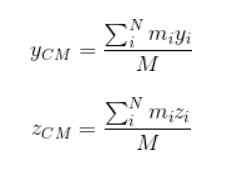
Váhový faktor v tomto prípade je hmotnosť každej z častíc, ktoré tvoria rozšírený objekt.

Môže vám slúžiť: Transcendentné funkcie: typy, definícia, vlastnosti, príklady

Dôležité charakteristiky masového centra

Ak je počet častíc veľmi veľký, ide o súvislý objekt. V tomto prípade n → ∞ a súčet sa nahradí definovaným integrálom, ktorého limity sú dané veľkosťou objektu.

Je dôležité zdôrazniť skutočnosť, že v mieste hromadného centra nemusí byť nevyhnutne hmotnosť. Napríklad v šiške šišky, centrum hmoty sa zhoduje viac -menej s geometrickým centrom Rosquilly.

Obrázok 2. Hromadné centrum šišky, pomerne symetrický objekt, je v diere. Zdroj: Pixabay.

Poloha hmotnostného centra nezávisí od referenčného systému používaného na stanovenie pozícií častíc, pretože ide o vlastnosť, ktorá závisí od samotnej konfigurácie objektu a nie od toho, ako je videný z rôznych referenčných rámcov.

Vyriešené cvičenia

- Cvičenie 1

V mnohých prípadoch učitelia priraďujú každej hodnotiacej činnosti na svojej stoličke rôzne váhy alebo percentuálne podiely. Napríklad, úlohy majú percento, ďalšie rôzne skúšky a koncová skúška, ktorá je pravdepodobne oveľa väčšia.

Obrázok 3. Vo svojich hodnotiacich plánoch učitelia zvyčajne priraďujú k hodnoteniu rôzne váhy. Zdroj: Kniha triedy od Davida Muldera cez Flickr.

Predpokladajme, že v určitom predmete sú hodnotiace činnosti a ich príslušné váhy nasledujúce:

-Domáce úlohy: 20 %

-Krátke skúšky: 25 %

-Laboratórne správy: 25 %

-Záverečná skúška: 30 %

a) Ako vypočíta učiteľ konečnú známku tejto témy pre každého študenta?

b) Predpokladajme, že kvalifikácia konkrétneho študenta je na stupnici od 1 do 5:

-Úlohy: 5.0 bodov

-Krátke skúšky: 4.7 bodov

-Laboratórne správy: 4.2 body

-Záverečná skúška: 3.5 bodov

Môže vám slúžiť: ENEGON: Vlastnosti, ako vyrobiť engon, príklady

Nájdite poslednú poznámku študenta v tejto téme.

Riešenie

a) Každé hodnotenie má inú váhu, ktorú učiteľ pridelil podľa svojej zložitosti a vlastných kritérií. Týmto spôsobom sa konečné hodnotenie priamo vypočíta ako:

Definitívne = (x20 % úloh + krátke skúšky x25 % + správy x25 % + záverečná skúška x30 %) / 100

b) definitívne = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) Body = 4.275 bodov ≈ 4.3 body

- Cvičenie 2

Majitelia obchodu s odevmi kúpili džínsy od troch rôznych dodávateľov.

Prvý predal 12 jednotiek za cenu 15 EUR, druhé 20 jednotiek na 12.80 EUR a tretina kúpila veľa z 80 jednotiek o 11.50 EUR.

Aká je priemerná cena zaplatená majiteľmi obchodu za každého kovboja?

Riešenie

Xp = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 EUR

Hodnota každého kovboja je 12.11 EUR, bez ohľadu na to, že niektorí stoja o niečo viac a iné o niečo menej. Bolo by to úplne rovnaké, keby majitelia obchodu kúpili 112 džínsov od jedného dodávateľa, ktorý by ich predal v 12.11 € kus.

Odkazy

  1. Arvelo, a. Opatrenia centrálnej tendencie. Zdroj: Franavelo.Slovník.com
  2. Mendenhall, W. 1981. Štatistiky pre správu a ekonomiku. Tretí. vydanie. Redakčná skupina Iberoamerica.
  3. Moore, D. 2005. Uplatňovaná štatistika. Druhý. Vydanie.
  4. Triola, m. 2012. Štatistika. 11. Edimatizovať. Pearson Vzdelanie.
  5. Wikipedia. Vážený priemer. Zdroj: In.Wikipedia.orgán