Výpočet inverznej matrice a vyriešené cvičenie
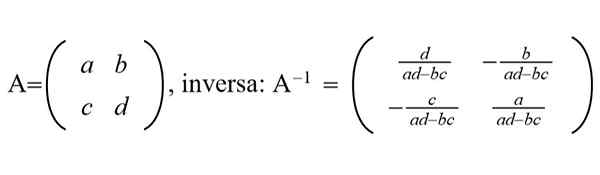
- 3121
- 186
- Valentín Dula
Ten Inverzná matica danej matice je to matica, ktorá sa vynásobí pôvodnými výsledkami v matici identity. Reverzná matica je užitočná na riešenie systémov lineárnych rovníc, a preto je dôležité vedieť, ako ju vypočítať.
Matice sú veľmi užitočné vo fyzike, inžinierstve a matematike, pretože sú kompaktným nástrojom na riešenie zložitých problémov. Užitočnosť matíc sa vylepšuje, keď sú nezvrátené a je známa aj ich inverzia.
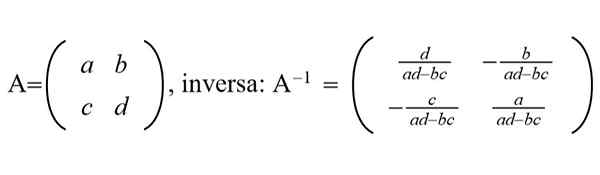 postava 1. Zobrazí sa generická matica 2 × 2 a jej inverzná matica. (Pripravil Ricardo Pérez)
postava 1. Zobrazí sa generická matica 2 × 2 a jej inverzná matica. (Pripravil Ricardo Pérez) V poliach grafického spracovania sa na vyhodnotenie inverznej matrice NXN s n veľmi veľké používajú efektívne a rýchle algoritmy na vyhodnotenie matíc matíc NXN s n veľmi veľkým, v poradí tisícov alebo miliónov nxn.
Na ilustráciu použitia reverznej matice v správe systému lineárnych rovníc začneme najjednoduchším prípadom všetkých: 1 × 1 matice.
Najjednoduchší prípad: Zohľadňuje sa lineárna rovnica jednej premennej: 2 x = 10.
Cieľom je nájsť hodnotu X, ale bude to „maticle“.
Matica M = (2), ktorá vynásobí vektor (x), je matica 1 × 1, ktorá vedie k vektore (10):
M (x) = (10)
Inverzia matice m je označená m-1.
Všeobecný spôsob písania tohto „lineárneho systému“ je:
M x = b, kde x je vektor (x) a b je vektor (10).
Podľa definície je reverzná matica, ktorá vynásobená pôvodnou matricou vedie v matici identity I:
M-1 M = i
V uvažovanom prípade matica m-1 Je to matica (½), ktorá je m-1 = (½) od m-1 M = (½) (2) = (1) = i
Môže vám slúžiť: 90 deliteľov: Čo sú a vysvetlenieAk chcete nájsť neznámy vektor x = (x), v vyvýšenej rovnici sú obaja členovia vynásobení reverznou maticou:
M-1 M (x) = m-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
Bola dosiahnutá rovnosť dvoch vektorov, ktoré sú rovnaké iba vtedy, keď sú ich zodpovedajúce prvky rovnaké, to je x = 5.
Výpočet inverzie matrice
Čo motivuje výpočet reverznej matice, je nájsť univerzálnu metódu riešenia lineárnych systémov, ako je napríklad nasledujúci systém 2 × 2:
x - 2 y = 3
-x + y = -2
Podľa krokov prípadu 1 × 1, ktorý sa študoval v predchádzajúcej časti, píšeme systém rovníc maticovým spôsobom:
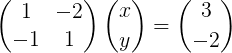 Obrázok 2. Lineárny systém vo forme matrice.
Obrázok 2. Lineárny systém vo forme matrice. Všimnite si, že tento systém je napísaný v kompaktnom vektorovom zápise takto:
M x = b
kde
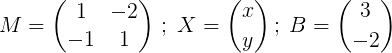
Ďalším krokom je nájsť m.
Metóda 1: Prostredníctvom gaussovského eliminácie
Použije sa metóda eliminácie Gauss. Ktorý spočíva v vykonávaní základných operácií v radoch matice, tieto operácie sú:
- Vynásobte riadok na ne -nulové číslo.
- Pridajte alebo odčítajte iný riadok alebo násobok iného riadku.
- Výmenné riadky.
Cieľom je prostredníctvom týchto operácií previesť pôvodnú maticu na maticu identity.
Ako sa to robí, v matici M sa uplatňujú presne rovnaké operácie v matici identity. Keď sa po niekoľkých operáciách v radoch RS transformuje na jednotnú maticu, potom sa pôvodne unitárny transformuje do reverznej matice m, tj M, m-1.
Môže vám slúžiť: Corollry (Geometry)1- Tento proces začíname napísaním matice M a vedľa nej matica jednotky:
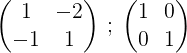
2- Pridáme dva riadky a výsledok je uvedený do druhého riadku, týmto spôsobom získame nulu v prvom prvku druhého riadku:
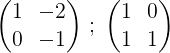
3 - Vynásobíme druhý riadok -1, aby sme získali 0 a 1 v druhom riadku:
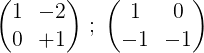
4- Prvý riadok sa vynásobí ½:

5- Druhý a prvý z nich pridá a výsledok je umiestnený v prednom riadku:
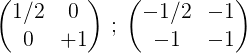
6- Na ukončenie procesu sa vynásobí prvý riadok po 2, aby sa získal v prvej matici identity a v druhej reverznej matici pôvodnej matice M:
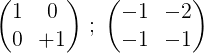
To znamená:
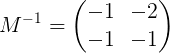
Riešenie systému
Po získaní spätnej matice sa systém rovníc vyrieši použitím reverznej matice v oboch členoch kompaktnej vektorovej rovnice:
M-1M x = m-1B
X = m-1B
To výslovne zostáva takto:
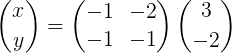
Potom sa vynásobí matrica, aby sa získal vektor x:
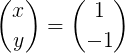
Metóda 2: Pripojenou maticou
V tejto druhej metóde sa spočítaná matica vypočíta na základe pripojenej matice pôvodnej matrice Do.
Predpokladajme, že matica daná:

kdeJa, J Je to prvok riadku Jo a stĺpec J matrice Do.
Pripevnenie matrice Do Bude sa to volať Adj (a) A jeho prvky sú:
ReklamaJa, J = (-1)(i+j) ¡
kde Ai, j Je to doplnková menšia matica, ktorá sa získa eliminovaním riadku I a stĺpca J z pôvodnej matrice Do. Stĺpce ¡naznačujú, že sa vypočíta determinant, to znamená ¡ Je to determinant doplnkovej menšej matrice.
Môže vám slúžiť: homológne stranyInverzná matrica
Vzorec na nájdenie reverznej matice založenej na pripojenej matici pôvodnej matice je nasledujúci:
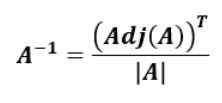
To znamená, že reverzná matica Do, Do-1, je transpozícia pripútanosti Do rozdelený determinantom Do.
Transponovaný DoTónmatrice Do Je to ten získaný výmenou hodností za stĺpce, to znamená, že prvý riadok sa stáva prvým stĺpcom a druhým riadkom do druhého stĺpca atď.
Cvičenie
Buďte maticou k ďalšej:
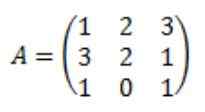
Každý z prvkov pripojenej matice A: adj (a)
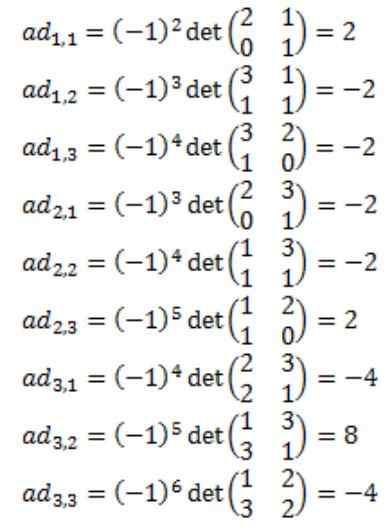
Výsledkom toho, že pripojená matica A, adj (a) je nasledovná:
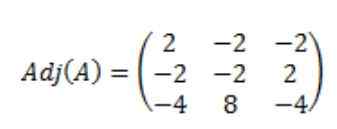
Potom sa vypočíta determinant matice A, deta (a):
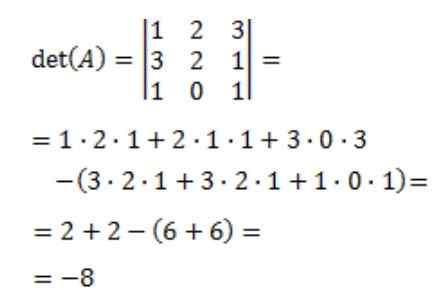
Nakoniec sa získa reverzná matica A:
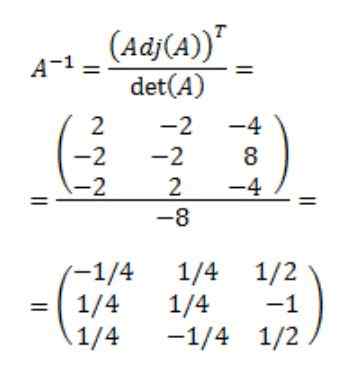
Odkazy
- Anthony Nicolaides (1994) Determinanty a matice. Publikácia.
- Awol Assen (2013) Štúdia o výpočte determinantov 3 × 3
- Casteleiro Villalba m. (2004) Úvod do lineárnej algebry. Redakcia.
- Dave Kirkby (2004) Maths Connect. Výtvarník.
- Jenny Olive (1998) Maths: Sprievodca prežitím študenta. Cambridge University Press.
- Richard J. Brown (2012) 30-sekundová matematika: 50 najvýznamnejších teórií matematiky. Ivy Press Limited.
- Matica. Lap Lambert Academic Publishing.
- « Charakteristiky polovičného kultivačného média, typy, použitie
- Popis mayského kalendára, ako funguje, systémy »

