Diskrétna matematika

Čo sú diskrétna matematika?

Ten diskrétna matematika zodpovedá oblasti matematiky, ktorá je zodpovedná za štúdium súboru prírodných čísel; To znamená, že súbor konečných a nekonečných účtovných čísel, kde sa prvky môžu počítať osobitne, jeden po jednom.

Tieto sady sú známe ako diskrétne sady; Príkladom týchto súborov sú celé čísla, grafy alebo logické výrazy a používajú sa v rôznych vedeckých oblastiach, najmä v oblasti informatiky alebo výpočtovej techniky.

Opis

V diskrétnej matematike sú procesy počítané, sú založené na celých číslach. To znamená, že desatinné čísla sa nepoužívajú, a preto sa nepoužíva prístup alebo limity, ako v iných oblastiach. Napríklad neznáme sa môže rovnať 5 alebo 6, ale nikdy 4,99 alebo 5,9.

Na druhej strane, v grafickej reprezentácii budú premenné diskrétne a sú uvedené z konečnej sady bodov, ktoré sa počítajú jeden po druhom, ako je pozorované na obrázku:

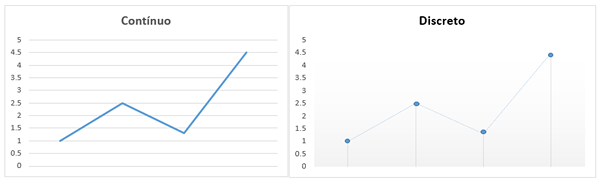
Diskrétna matematika sa rodí z dôvodu potreby získať presnú štúdiu, ktorú je možné kombinovať a dokázať, aby ju uplatnila v rôznych oblastiach.

Na čo sú diskrétna matematika?

Diskrétna matematika sa používa vo viacerých oblastiach. Medzi hlavnými patrí:

Kombinačný

Študovať konečné súbory, kde je možné prvky objednať alebo kombinovať a vyvolať.

Teória diskrétnej distribúcie

Študijné udalosti, ktoré sa vyskytujú v priestoroch, kde môžu byť vzorky účtovníctvo, v ktorých sa nepretržité rozdelenie používajú na oslovenie diskrétnych distribúcií alebo naopak.

Teória informácií

Vzťahuje sa na kódovanie informácií, ktoré sa používa na návrh a prenos a ukladanie údajov, napríklad podobné signály.

Výpočtový

Prostredníctvom diskrétnej matematiky sa problémy riešia pomocou algoritmov, ako aj to, čo je možné vypočítať a čas potrebný na to, aby sa to stalo (zložitosť).

Dôležitosť diskrétnej matematiky v tejto oblasti sa v posledných desaťročiach zvýšila, najmä pre rozvoj programovania a Softvér.

Kryptografia

Je založená na diskrétnej matematike na vytváranie bezpečnostných štruktúr alebo metód šifrovania. Príkladom tejto aplikácie sú heslá, ktoré odosielajú samostatné bity, ktoré obsahujú informácie.

Prostredníctvom štúdie je možné vytvoriť alebo zničiť vlastnosti celých čísel a prvých čísel (teória čísel).

Logika

Používajú sa diskrétne štruktúry, ktoré zvyčajne tvoria konečnú sadu, aby sa demonštrovali vety alebo napríklad overovanie softvéru.

Teória grafov

Umožňuje rozlíšenie logických problémov pomocou uzlov a riadkov, ktoré tvoria typ grafu, ako je to znázornené na nasledujúcom obrázku:

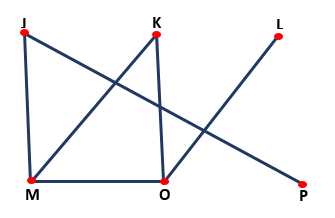Algebra

Je to oblasť úzko spojená s diskrétnou matematikou, pretože algebraické výrazy sú diskrétne. Prostredníctvom týchto elektronických obvodov sa vyvíjajú procesory, programovanie (booleovská algebra) a databázy (relačná algebra) (relačná algebra).

Geometria

Študujte kombinatorické vlastnosti geometrických objektov, ako je napríklad povlak roviny. Na druhej strane výpočtová geometria umožňuje vyvíjať geometrické problémy s použitím algoritmov.

Teória

V diskrétnej matematike sú sady (konečné a nekonečné znecitlivenie) hlavným objektívnym cieľom. Teória súboru publikovala George Cantor, ktorý ukázal, že všetky nekonečné súpravy majú rovnakú veľkosť.

Sada je skupina prvkov (čísla, veci, zvieratá a ľudia, okrem iného), ktoré sú dobre definované; to znamená, že existuje vzťah, podľa ktorého každý prvok patrí do súboru a je vyjadrený napríklad A ∈ A.

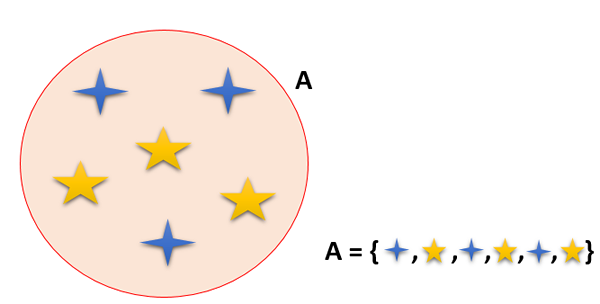
V matematike existujú rôzne súbory, ktoré zoskupujú určité čísla podľa svojich charakteristík. Napríklad majú:

- Sada prírodných čísel n = 0, 1, 2, 3, 4, 5, 6,… +∞.

- Sada celých čísel e = -∞…, -3, -2, -1, 0, 1, 2, 3,… +∞.

- Podskupina racionálnych čísel q* = -∞…, - ¼, - ½, 0, ¼, ½, ... ∞.

- Sada skutočných čísel r = -∞…, -½, -1, 0, ½, 1,… ∞.

Sady sú pomenované s abecednými písmenami v kapitálových písmenách; Zatiaľ čo prvky sú pomenované malými písmenami, vnútorné kľúče () a oddelené čiarkami (,). Spravidla sú zastúpené na diagramoch ako Venn a Caroll, ako aj výpočtovo.

Pri základných operáciách, ako sú únia, križovatka, doplnok, rozdiel a karteziánsky produkt, sú sety a ich prvky spravované na základe príslušného vzťahu.

Existuje niekoľko druhov sád, najviac študovaných v diskrétnej matematike sú nasledujúce:

Konečná súprava

Je to ten, ktorý má konečný počet prvkov a ktorý zodpovedá prirodzenému číslu. Napríklad a = 1, 2, 3,4 je konečná sada, ktorá má 4 prvky.

Nekonečný účtovný súbor

Je to jeden, v ktorom existuje korešpondencia medzi prvkami množiny a prírodnými číslami; to znamená, že zo prvku sú všetky prvky množiny uvedené postupne.

Týmto spôsobom bude každý prvok zodpovedať každému prvku množiny prírodných čísel. Napríklad:

Celé celé čísla z = … -2, -1, 0, 1, 2… sa dá uviesť ako z = 0, 1, -1, 2, -2…. Týmto spôsobom je možné vytvoriť jednorazovú korešpondenciu medzi prvkami Z a prírodnými číslami, ako je vidieť na nasledujúcom obrázku:

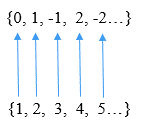Diskrétnosť

Je to metóda používaná na riešenie kontinuálnych problémov (modely a rovnice), ktorá sa musí premieňať na diskrétne problémy, v ktorých je riešenie známe s prístupom k riešeniu nepretržitého problému.

V opačnom prípade sa diskretizácia snaží získať konečné množstvo nekonečného súboru bodov; Týmto spôsobom sa kontinuálna jednotka transformuje na jednotlivé jednotky.

Všeobecne sa táto metóda používa v numerickej analýze, napríklad v riešení diferenciálnej rovnice, prostredníctvom funkcie, ktorá je reprezentovaná konečným množstvom údajov vo svojej doméne, aj keď je to nepretržité.

Ďalším príkladom diskretizácie je jej použitie na premenu analogického digitálneho signálu, keď sa kontinuálne signálne jednotky prevedú na jednotlivé jednotky (sú diskretizované) a potom kódované a kvantifikované, aby sa získal digitálny signál.

Odkazy

1. Grimaldi, R. P. (1997). Diskrétna a kombinatorická matematika. Redakcia Addison Wesley Iberoamericana.
2. Ferrando, V. Gregori. (Devätnásť deväťdesiatpäť). Diskrétna matematika. Reverzný.
3. Jech, T. (2011). Teória. Stanfordská encyklopédia filozofie.
4. José Francisco Villalpando Becerra, a. G. (2014). Diskrétna matematika: aplikácie a cvičenia. Redakčná skupina Patria.
5. Landau, r. (2005). Výpočet, do prvého kurzu vo vedeckom.
6. Merayo, f. G. (2005). Diskrétna matematika. Thomson redaktor.
7. Rosen, K. H. (2003). Diskrétna matematika a jej aplikácie. Redakcia McGraw-Hill.
8. Schneider, D. G. (Devätnásť deväťdesiatpäť). Logický prístup k diskrétnej matematike.