Vektor

Čo je to vektor?

A Vektor Je to akýkoľvek výraz predstavovaný vektorom, ktorý má numerickú hodnotu (modul), smer, smer a bod aplikácie. Niektoré príklady vektorových veľkostí sú posunutie, rýchlosť, pevnosť a elektrické pole.

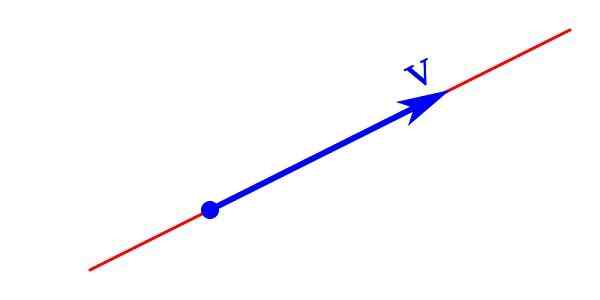
Grafické znázornenie veľkosti vektora pozostáva zo šípky, ktorej špička označuje jej smer a smer, jeho dĺžka je modul a východiskovým bodom je pôvod alebo bod aplikácie.

Grafické znázornenie vektora

Veľkosť vektora je analyticky reprezentovaná písmenom, ktorý nesie šípku v hornej časti smerom doprava v horizontálnom smere. Môže byť tiež reprezentovaný listom napísaným tučným písmom Vložka ktorého modul ǀVložkaǀ Je napísaná kurzívou Vložka.

Jednou z aplikácií koncepcie vektorovej veľkosti je návrh diaľnic a ciest, konkrétne pri návrhu svojich zakrivení. Ďalšou aplikáciou je výpočet posunu medzi dvoma miestami alebo zmena rýchlosti vozidla.

Prvky vektorovej veľkosti

Vektorová veľkosť je akákoľvek entita predstavovaná linkovým segmentom s orientáciou vo vesmíre, ktorý má charakteristiky vektora. Jeho prvky sú:

Modul: Je to numerická hodnota, ktorá označuje veľkosť alebo intenzitu veľkosti vektora.

Osloviť: Je to orientácia segmentu čiary v priestore, ktorá ho obsahuje. Vektor môže mať horizontálny, vertikálny alebo naklonený smer; Sever, juh, tento alebo západ; Severovýchodný, juhovýchodný, juhozápadný alebo severozápad.

Zmysel: Je označený špičkou šípky na konci vektora.

Môže vám slúžiť: fyzika pred Grékmi (Antigua Grécko)

Aplikačný bod: Je to pôvod alebo bod počiatočného pôsobenia vektora.

Klasifikácia vektorov

Vektory sú klasifikované ako kolineárne, rovnobežné, kolmé, súbežné, spojky, voľné, kĺzanie, oproti, vybavenie, pevné a jednotky.

Kolineal: Patrí alebo konajú na rovnakej priamke, nazývajú sa tiež lineárne závislý A môžu byť vertikálne, vodorovné a naklonené.

Paralely: Majú rovnakú adresu alebo sklon.

Kolmý: Dva vektory sú navzájom kolmé, keď je uhol medzi nimi 90 °.

Súbežný: Sú to vektory, ktoré pri posúvaní ich konania sa zhodujú v rovnakom bode vesmíru.

Koplanáriá: Konajú v lietadle, napríklad lietadlo Xy.

zadarmo: Pohybujú sa kdekoľvek v priestore a udržiavajú svoj modul, smer a význam.

Šmykľavka: Pohybujú sa po rade akcie určenej ich smerom.

Protiklady: Majú rovnaký modul a smer a opačný smer.

Vybavenie: Majú rovnaký modul, smer a význam.

Stanovený: Bod aplikácie je nemenný.

Jednotka: Vektory, ktorých modul je jednotka.

Vektorové komponenty

Vektorová veľkosť v trojrozmernom priestore je znázornená v systéme troch osí kolmých na seba (X a z) sa nazýva ortogonal pokus.

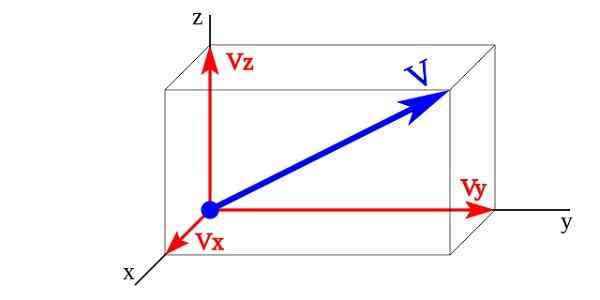Vektorové komponenty vektorovej veľkosti

Na obrázku vektory Vx, Hnedý, VZ sú vektorové vektorové komponenty Vložka ktorých jednotkové vektory sú X,a,z. Vektor Vložka Je zastúpený súčtom svojich vektorových komponentov.

Vložka = Vx + Hnedý + VZ

Výsledkom niekoľkých vektorových veľkostí je vektorový súčet všetkých vektorov a nahrádza tieto vektory v systéme.

Vektorové pole

Vektorové pole je oblasť priestoru, v ktorej v každom z jeho bodov vektorová veľkosť zodpovedá. Ak sa prejavuje veľkosť, ktorá je silou pôsobiacou na telo alebo fyzikálny systém, potom je pole vektorov poľom sily.

Môže vám slúžiť: Steinerova veta: Vysvetlenie, aplikácie, cvičenia

Vektorové pole je graficky reprezentované polí čiarami, ktoré sú dotykovou čiarou vektorovej veľkosti vo všetkých bodoch v regióne. Niektoré príklady vektorových polí sú elektrické pole vytvorené presným elektrickým nábojom v priestore a rýchlostnej oblasti tekutiny.

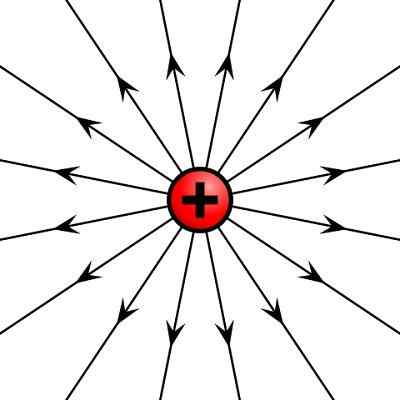Elektrické pole vytvorené kladným elektrickým nábojom

Operácie s vektormi

Pridanie vektorov: Je to výsledok dvoch alebo viacerých vektorov. Ak máte dva vektory Ani a P Suma je Ani + P = q. Vektor Otázka Je to výsledný vektor, ktorý sa získa graficky pohybujúci sa pôvod vektora Do do konca vektora B.

Odčítanie vektorov: Odčítanie dvoch vektorov alebo a P je Ani - P = Q. Vektor Otázka  Dostanete pridanie do vektora Ani Tvoj oproti -P. Grafická metóda je rovnaká ako súčet s rozdielom, že opačný vektor sa prenáša do extrému.

Skalárny produkt: Produkt skalárnej veľkosti do vektor P Je to vektor Mp ktorý má rovnaký smer vektora P. Ak je skalárna veľkosť nula, skalárny produkt je nulová vektor.

Príklady vektorových veľkostí

Pozícia

Poloha objektu alebo častice vzhľadom na referenčný systém je vektor, ktorý je daný jeho pravouhlými súradnicami X a z, a je zastúpený jeho vektorovými komponentmi Xî, Yĵ, Zk. Vektory  Jo, ĵ, klimatizovať Sú jednotkovými vektormi.

Častica v jednom bode (X a z) má polohový vektor r = Xî + Yĵ + Zk. Numerická hodnota vektorovej polohy je r= √ (X² + a² + z²). Zmena polohy častíc z jednej polohy na druhú vzhľadom na referenčný systém je vektor Posun ΔR A vypočíta sa s nasledujúcim vektorovým výrazom:

Môže vám slúžiť: anodické lúče

Δr = r₂ - r₁

Zrýchlenie

Priemerné zrýchlenie (do_m) Je definovaný ako variácia rýchlosti vložka V časovom intervale Δt A výraz na jeho výpočet do_m= ΔV/Δt, bytosť ΔV Rýchlosť zmeny vektora.

Okamžité zrýchlenie (do) je limit priemerného zrýchlenia do_m kedy Δt stáva sa tak malým, že má tendenciu nula. Okamžité zrýchlenie je vyjadrené podľa jeho vektorových komponentov

do =do_XJo +do_a ĵ+ do_zklimatizovať

Gravitačné pole

Sila gravitačnej príťažlivosti vyvíjaná hmotnosťou M, Nachádza sa pri pôvode, na inej omši m V jednom okamihu vesmíru X, a, z Je to vektorové pole nazývané gravitačné silové pole. Táto sila je daná výrazom:

F= (-mmg/r)ȓ

r = Xî + Yĵ + Zk

F = Je to gravitačná sila fyzickej veľkosti

G = je univerzálna gravitačná konštanta

ȓ = je vektor hmotnostnej polohy m

Odkazy

1. Tallack, J C. Úvod do vektorovej analýzy. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S a Spellman, D. Vektor. siež.l. : MC Graw Hill, 2009.
3. Značka, L. Vektor. New York: Dover Publications, 2006.
4. Griffiths, D J. Úvod do Electodynamics. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Haag, b. Úvod do vektorovej analýzy. Glasgow: Methuen & Co. Ltd, 2012.