Fermat Limit to, čo pozostáva, a cvičenia vyriešili

On Limit Je to numerická metóda, ktorá sa používa na dosiahnutie hodnoty sklonu čiary, ktorá je dotýkaná špecifickej funkcii jej domény. Používa sa tiež pri získavaní kritických bodov funkcie. Jeho výraz je definovaný ako:

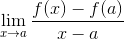
Je zrejmé, že Fermat nepoznal základy derivácie, avšak práve jeho štúdia podporila skupinu matematikov, aby sa pýtali na tangenciály a ich aplikácie pri výpočte.

[TOC]

Aký je limit Fermat?

Skladá sa z prístupu 2 bodov, ktorý v predchádzajúcich podmienkach tvorí sekundárnu líniu funkcie s križovatkou v pároch hodnôt.

Keď sa blíži k premennej k hodnote „A“, pár bodov je povinný splniť. Týmto spôsobom sa predtým sušiaca čiara stáva dotykovou bodom (a; f (a)).

Hodnota kvocientu (x - a), keď je vyhodnotená v bode „A“, vyvolá neurčitosť limitov typu K medzi nulou (k/0). Kde tieto neurčity môžu byť prerušené rôznymi technikami faktorizácie.

Najpoužívanejšie prevádzkové techniky sú:

-Štvorcový rozdiel (a² - b² ) = (a + b) (a - b); Existencia prvku (A-B) vo väčšine prípadov naznačuje faktor, ktorý zjednodušuje expresiu (X-A) v limitovom pomere Fermat.

- Štvorcové dokončenie (sekera² + bx); Po dokončení štvorcov sa získa Newton Binomial, kde je jeden z jeho 2 faktorov zjednodušený výrazom (x - a), ktorý prelomí neurčitosť.

- Konjugát (a + b) / (a ​​+ b); Vynásobenie a rozdelenie výrazu konjugátom určitého faktora môže byť veľmi pomáhať prelomiť neurčitosť.

- Spoločný faktor; V mnohých prípadoch výsledok prevádzky čitateľa Fermat F (x) - f (a) skrytý k faktoru (x - a) potrebný na faktorizáciu. Z tohto dôvodu sa pozorne pozoruje, aké prvky sa opakujú v každom faktore expresie.

Fermat Limit Application pre maximálne a minimum

Aj keď limit Fermat nerozlišuje medzi maximálnym a minimálnym.

Základné znalosti o grafickej teórii funkcií pri konundingu s touto vetou môžu byť dostatočné na stanovenie maximálnych a minimálnych hodnôt medzi funkciami. V skutočnosti možno inflexné body definovať vetou dodatočnej priemernej hodnoty pre Fermatovu vetu.

Kubické podobenstvo

Najvýznamnejší paradox pre Fermat prišiel pri štúdiu kubického podobenstva. Pretože jeho pozornosť bola zameraná na dotyčničné línie funkcie pre daný bod, narazil na problém definovania uvedenej dotyčnice v existujúcom inflexnom mieste vo funkcii.

Zdalo sa nemožné určiť dotyčničku do bodu. Tak začína vyšetrovanie, ktoré by viedlo k rozlišovaciemu počtu. Potom definované dôležitými exponentmi matematiky.

Maximus a minimálny

Štúdium maximálneho a minimum funkcie bolo výzvou pre klasickú matematiku, kde jednoznačná a praktická metóda pre definíciu týchto.

Fermat vytvoril metódu založenú na prevádzke malých diferenciálnych hodnôt, ktoré sa po faktorizačných procesoch eliminujú tým, že ustúpili najväčšej a minimálnej hodnote.

Táto premenná sa musí vyhodnotiť v pôvodnom expresii, aby sa určila súradnica uvedeného bodu, ktorý spolu s analytickými kritériami bude definovaný maximálnym alebo minimom expresie.

Metóda

Vo svojej metóde Fermat používa vietinú doslovnú symboliku, ktorá pozostávala z výhradného použitia kapitálových písmen: samohlásky, pre neznámych a spoluhlásky pre známe množstvá.

V prípade radikálnych hodnôt Fermat implementoval konkrétny proces, ktorý by sa neskôr použil pri faktorizácii limitov neurčitosti nekonečno medzi nekonečnosťou.

Tento proces pozostáva z rozdelenia každého výrazu pomocou použitej diferenciálnej hodnoty. V prípade Fermata použila písmeno E, kde po rozdelení medzi najväčšou silou E sa hodnota požadovaná z kritického bodu jasne vyjasní.

História

Limit Fermat je v skutočnosti jedným z najmenej renomovaných príspevkov v dlhom zozname matematikov. Jeho štúdie boli z hlavných čísel, aby v podstate vytvorili základy na výpočet.

Na druhej strane bol Fermat známy svojimi excentricitami, pokiaľ ide o jeho hypotézy. Bolo to bežné pre určitú výzvu pre ostatných matematikov času, keď už mal riešenie alebo demonštráciu.

Mal veľké množstvo sporov a aliancií s rôznymi matematikmi tej doby, ktorí s ním milovali alebo nenávidia prácu.

Jeho posledná veta bola hlavnou zodpovednosťou za jeho svetovú slávu, kde povedal, že zovšeobecnenie Pythagorová veta Pre akýkoľvek titul „n“ to nebolo možné. Povedal, že má platnú demonštráciu, ale zomrel pred zverejnením.

Táto demonštrácia musela čakať približne 350 rokov. V roku 1995 matematici Andrew Wiles a Richard Taylor ukončili úzkosť Fermat, čo preukázalo, že bol priamo prostredníctvom platnej demonštrácie svojej poslednej vety.

Cvičenia

Cvičenie 1

Definujte sklon čiary dotyčnej krivke f (x) = x² V bode (4, 16)

Výmena vo výraze limitu fermat, ktorý máte:

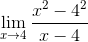
Potom použijete štvorcové minimá, čitateľ je faktor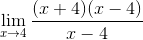

Faktory sú zjednodušené (x - 4)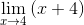

Pri hodnotení máte

M = 4 + 4 = 8

Cvičenie 2

Definujte kritický bod expresie f (x) = x² + 4x pomocou limitu Fermat

V tomto prípade neexistuje súradnica, takže hodnota X je nahradená všeobecným formulárom X₀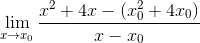

Vykonáva sa strategické zoskupenie prvkov a snaží sa zoskupovať kolegov X-X₀

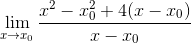
Rozvíjajú sa štvorce

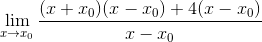
Pozoruje sa spoločný faktor x-x_{0 a je extrahovaný}

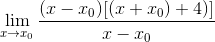
Výraz sa už môže zjednodušiť a neurčitosť je prerušená

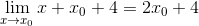
V minimálnych bodoch je známe, že sklon tangenciálnej čiary sa rovná nule. Týmto spôsobom môžeme zladiť nulu, ktorý sa nachádza a vymažeme hodnotu x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Ak chcete získať chýbajúcu súradnicu, musíte vyhodnotiť iba bod v pôvodnej funkcii

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Kritický bod je P (-2, -4).

Odkazy

1. Skutočná analýza. Historický prístup Sauhl Stahl, John Wiley & Sons, 5. augusta. 1999.
2. Matematická kariéra Pierra od Fermata, 1601-1665: Druhé vydanie. Michael Sean Mahoney. Princeton University Press, 5. júna. 2018
3. Od Fermat po Minkowski: Prednášky o teórii čísel a jej historickom vývoji. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Fermatova posledná veta: genetický úvod do teórie algebraických čísel. Harold M. Edward. Springer Science & Business Media, 14. januára. 2000
5. Fermat Days 85: Matematika pre optimalizáciu. J.-B. Hiriart-Uruty Elsevier, 1. januára. 1986