Blokujte prvky algebry, príklady, cvičenia vyriešené

On Blokovať algebru Vzťahuje sa na súbor operácií, ktoré sa vykonávajú prostredníctvom blokov. Tieto a niektoré ďalšie prvky slúžia na schematické predstavenie systému a ľahko vizualizáciu vašej reakcie na konkrétny záznam.

Všeobecne platí, že systém obsahuje rôzne elektrické, elektronické a elektromechanické prvky a každý z nich, s ich príslušnou funkciou a polohou v systéme, ako aj spôsob, akým súvisia, je schematizovaný prostredníctvom funkčných blokov.

postava 1.

Na obrázku vyššie je veľmi jednoduchý systém, ktorý pozostáva z vstupného signálu x (s), ktorý vstupuje do bloku s funkciami prenosu G (funkcie), ktorý ho upravuje a vytvára výstup y (s).

Je vhodné reprezentovať signály a ich cestu cez systém cez šípky, ktoré vstupujú a opúšťajú každý blok. Zvyčajne je tok signálu nasmerovaný zľava doprava.

Výhodou tohto druhu schémy je vizuálna pomoc, ktorú poskytuje pri porozumení systému, hoci to nepredstavuje fyzickú reprezentáciu toho istého. V skutočnosti je blokový diagram jedinečný, pretože podľa hľadiska je možné nakresliť aj niekoľko diagramov toho istého systému.

Môže sa tiež stať, že rovnaký diagram sa používa pre niekoľko systémov, ktoré sa navzájom nevyhnutne netýkajú, za predpokladu, že jeho správanie správne popisuje. Existujú rôzne systémy, ktorých reakcia je v mnohých aspektoch podobná, napríklad obvod LC (induktor-kanál) a systém s hmotnosťou.

[TOC]

Čo je bloková schéma?

Systémy sú zvyčajne komplikovanejšie ako na obrázku 1, ale bloková algebra poskytuje sériu jednoduchých pravidiel na manipuláciu so systémovou schémou a jeho redukciu na najjednoduchšiu verziu.

Ako je vysvetlené na začiatku, diagram používa bloky, šípky a kruhy na vytvorenie vzťahu medzi každým systémovým komponentom a tokom signálov, ktoré cez ňu prechádzajú.

Bloková algebra umožňuje porovnávať dva alebo viac signálov prostredníctvom súčtu, odčítania a násobenia z nich, ako aj analyzovať príspevok, ktorý každý komponent poskytuje do systému.

Vďaka tomu je možné zredukovať celý systém na jeden vstupný signál, jedinečnú prenosovú funkciu, ktorá úplne popisuje akciu systému a zodpovedajúci výstup.

Môže vám slúžiť: Astroclymics: História, aké štúdie, vetvy

Prvky blokovej schémy

Prvky blokového diagramu sú nasledujúce:

Signál

Signály sú veľmi rozmanité, napríklad je bežné, že ide o elektrický prúd alebo napätie, ale môže byť jasný, zvuk a ďalšie. Dôležité je, že obsahuje informácie o určitom systéme.

Signál je označený kapitálom, ak je funkciou premennej siež Laplace transformácie: x (s) (pozri obrázok 1) alebo s malými písmenami, ak je založený na čase tón, ako x (t).

V blokovom diagrame je vstupný signál reprezentovaný šípkou nasmerovanou smerom k bloku, zatiaľ čo výstupný signál označený ako y (s) alebo (t) je označený odchádzajúcou šípkou.

Vstupný aj výstupný signál je jedinečný a adresa, v ktorej sú informácie určené smerom šípky. A algebra je rovnaká pre jednu z týchto dvoch premenných.

Blok

Blok je reprezentovaný štvorcovým alebo obdĺžnikovým (pozri obrázok 1) a môže sa použiť na vykonávanie operácií alebo na implementáciu prenosovej funkcie, ktorá sa zvyčajne označuje ako kapitálové písmeno G. Táto funkcia je matematický model, pomocou ktorého je odozva ponúkaná systémom opísaná pred vstupným signálom.

Funkcia prenosu môže byť vyjadrená z hľadiska času tón ako G (t) alebo premenná siež ako g (s).

Keď vstupný signál X (s) príde do bloku, vynásobí sa prenosovou funkciou a transformuje sa do výstupného signálu y (s). Matematicky sa vyjadruje takto:

A (s) = x (s).G (s)

Rovnako je prenosová funkcia pomerom medzi Laplace transformáciou výstupného signálu a Laplaceovou transformáciou vstupného signálu za predpokladu, že počiatočné podmienky systému sú nulové:

G (s) = y (s) / x (s)

Bod

Suma alebo leto je symbolizovaná kruhom s krížom vo vnútri. Používa sa na kombináciu sumy a odčítania, dva alebo viac signálov. Na konci šípky, ktorá symbolizuje signál, sa znak + umiestni priamo, ak sa tento signál pridá alebo znak - ak je odpočítaný.

Na nasledujúcom obrázku je príklad toho, ako leto funguje: máte vstupný signál X, ku ktorému sa pridávajú signály A a B, čo získava výstup a ktorý sa algebraicky rovná:

Môže vám slúžiť: vertikálny záber: vzorce, rovnice, príklady

Y = x+a+b

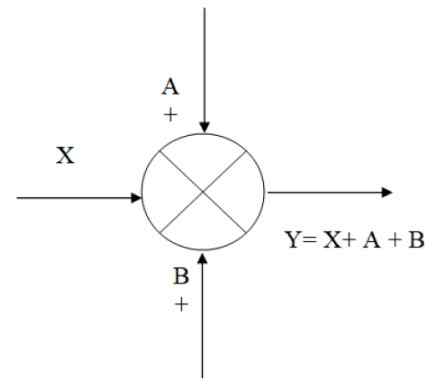Obrázok 2. Príklad presadzovania. Zdroj: f. Zapata.

Pobočka

Volá sa to tiež Rozmanitosť. V ňom je signál, ktorý vychádza z bloku, distribuovaný do iných blokov alebo do oblaku. Je reprezentovaný bodom umiestneným na šípke signálu a z nej pochádza ďalšia šípka, ktorá presmeruje signál smerom k inej časti.

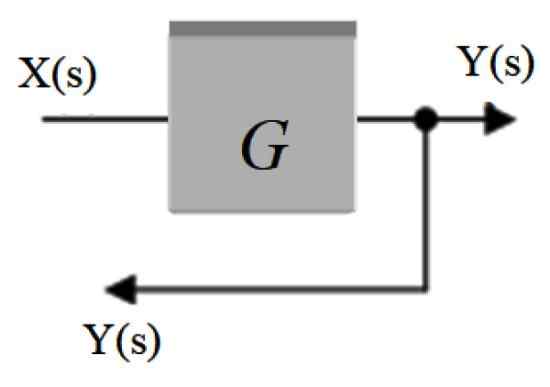Obrázok 3. Pobočka. Zdroj: f. Zapata.

Príklady blokov blokovej algebry

Ako už bolo vysvetlené, myšlienkou je vyjadriť systém cez blokový diagram a znížiť ho, aby ste našli funkciu prenosu, ktorá ju popisuje. Nasledujú pravidlá blokovej algebry na zjednodušenie diagramov:

Kaskádové bloky

Keď máte signál, ktorý postupne prechádza cez bloky G₁, G₂, G₃..., redukuje sa na jedinečný blok, ktorého funkcia prenosu je produktom G₁, G₂, G₃..

V nasledujúcom príklade signál x (s) vstupuje do prvého bloku a jeho výstup je:

A₁(s) = x (s).G₁(S)

Obrázok 4. Dva bloky vo vodopáde. Zdroj: f. Zapata.

Zase a₁(s) Zadajte blok G₂(s), ktorého odchod je:

A₂(s) = x (s).G₁(S). G₂(S)

Postup je platný pre bloky N Cascade:

A_n (s) = x (s). G₁(S).G₂(S) ... G_n(S)

Bloky paralelne

V ľavom diagrame signál X (S) Bifurca na vstup do blokov G₁(S) a g₂(S):

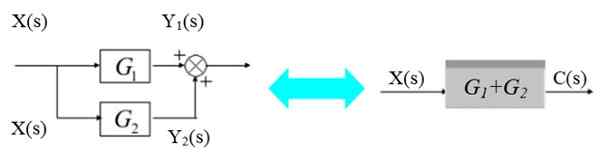Obrázok 5. Paralelne dva bloky. Zdroj: f. Zapata.

Príslušné výstupné signály sú:

A₁(s) = x (s).G₁(S)

A₂(s) = x (s).G₂(S)

Tieto signály sa pridávajú na získanie:

C (s) = y₁(s) +₂(s) = x (s).[G₁(s) + g₂(s)]]

Ako je znázornené v pravom diagrame.

Presuňte nápadníka doľava

Leto sa môže presunúť doľava od bloku nasledovne:

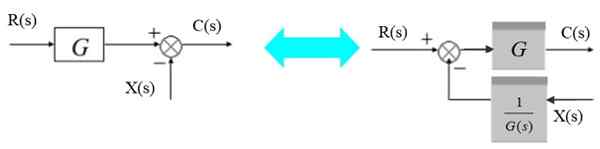Obrázok 6. Posuňte doplnok doľava od bloku. Zdroj: f. Zapata.

Vľavo je výstupný signál:

C (s) = r (s). G (s) - x (s)

Rovnocenné pravé:

C (s) = [r (s) - x (s)/g (s)]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]].G (s)

Presuňte doprava doprava

Leto sa môže pohybovať napravo od bloku, ako je toto:

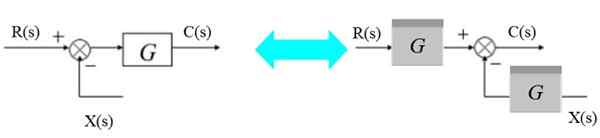Obrázok 7. Posuňte pozemok napravo od bloku. Zdroj: f. Zapata.

Vľavo máte: [r (s) - x (s)].G (s) = c (s)

Môže vám slúžiť: Princíp Archimedes: vzorec, demonštrácia, aplikácie

A napravo:

R (s). G (s) - x (s).G (s) = c (s)

Presunúť roz zaniknutie zľava doprava

Na vytesnenie rozhlasového bodu zľava doprava od bloku je dosť na to, aby ste si všimli, že výstup C (s) vpravo je produkt x (s).G (s). Ako sa chcete znova stať x (s), vynásobí sa inverziou g (s).

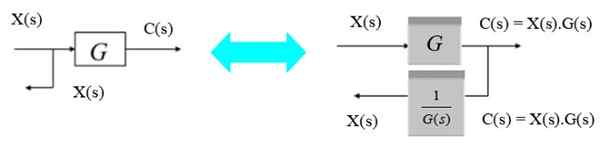Obrázok 8. Presunúť bod pobočky zľava doprava. Zdroj: f. Zapata.

Presuňte bifurkačný bod z pravej doľava

Alternatívne sa bod rozdvojenia môže presunúť z pravého doľava nasledovne:

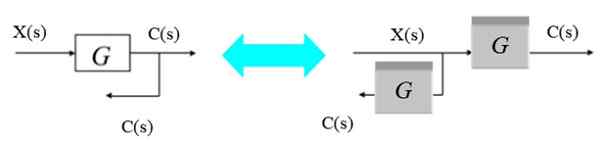Obrázok 9. Presuňte bod pobočky sprava doľava. Zdroj: f. Zapata.

Pretože výstup bifurkácie chce získať C (S), nový blok G (S) je jednoducho rozptýlený v rozponurkačnom bode naľavo od pôvodného bloku.

Systém so spätnou väzbou

V nasledujúcom systéme je výstupný signál C (s) podávaný cez submisívny vľavo:

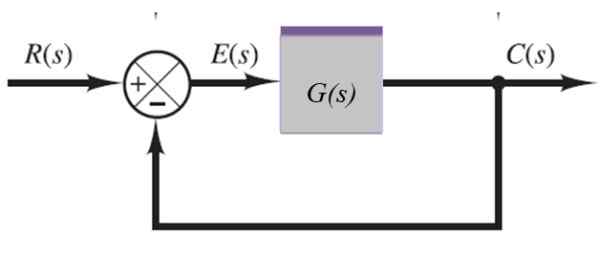Obrázok 10. Systém so spätnou väzbou. Zdroj: f. Zapata.

C (s) = e (s).G (s)

Ale:

E (s) = r (s) -c (s)

Nahradenie tohto výrazu v predchádzajúcej rovnici je: C (s) = [r (s) -c (s)]]]]]]]]]]]]]]].G (s), z ktorých je možné C (s) vyčistiť:

C (s) + c (s).G (s) = r (s).G (s) → c (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Alebo striedavo:

C (s) / r (s) = g (s) / [1 + g (s)]]

Graficky, po zjednodunutí je:

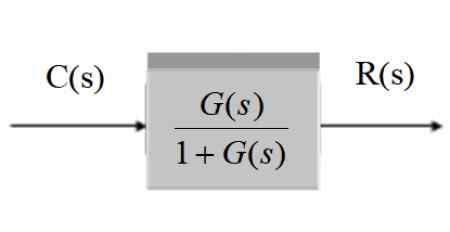Obrázok 11. Zjednodušenie systému so spätnou väzbou. Zdroj: f. Zapata.

Systém so spätnou väzbou a prevodníkom

Prevodník pozostáva z prenosovej funkcie H (s):

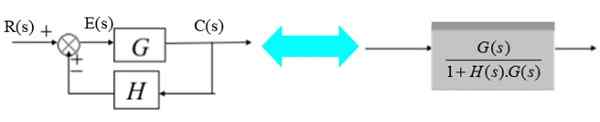Obrázok 12. Systém so spätnou väzbou a prevodníkom. Zdroj: f. Zapata.

V pravom diagrame je výstupný signál C (s):

C (s) = e (s). G (s) s e (s) = r (s) - c (s).H (s)

Tak:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ h (s).G (s)] = r (s).G (s)

Preto je možné C (s) vyčistiť:

C (s) = g (s).R (s) / [1+ h (s).G (s)]

A funkcia prenosu bude:

G (s) / [1+ h (s).G (s)]

Ako je znázornené v zjednodušenom pravom diagrame.

Vyriešené cvičenia

Cvičenie 1

Nájdite funkciu prenosu nasledujúceho systému:

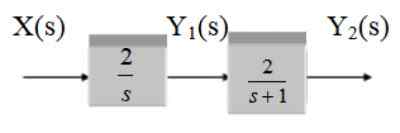Obrázok 13. Dva blokový systém vo vodopáde. Zdroj: f. Zapata.

Riešenie

Sú to dva kaskádové bloky, preto je funkcia prenosu produktom funkcií G₁ a g₂.

Musíš:

G₁ = 2/s

G₂ = 2 /(s+1)

Preto je vyhľadávaná funkcia prenosu:

G (s) = 4 / [s (s+1)]

Cvičenie 2

Znížte nasledujúci systém:

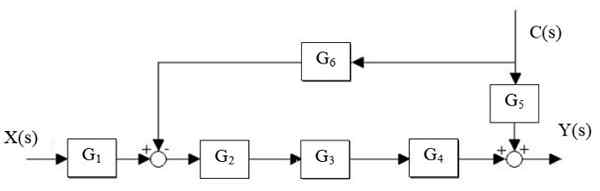Obrázok 14. Zjednodušenie systému. Zdroj: f. Zapata.

Riešenie

Najskôr sa zmenšuje kaskáda G₂, G₃ a g_4, A paralelný G je oddelený₅ a g₆:

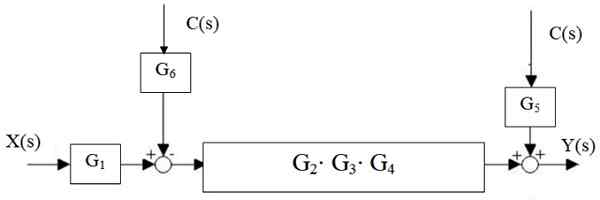Obrázok 15. Zníženie centrálneho vodopádu. Zdroj: f. Zapata.

Potom nápadník vľavo od bloku G₂ ⋅g₃ ⋅ g₄ Pohybuje sa doprava:

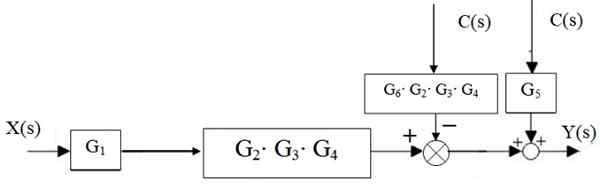Obrázok 16. Prenos správcu. Zdroj: f. Zapata.

Letá vpravo sú redukované na jedno, ako aj na kaskádové bloky:

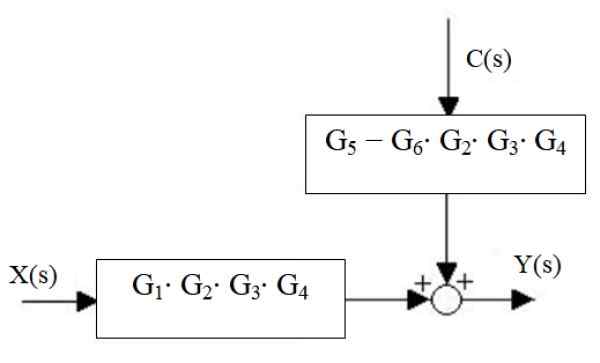Obrázok 17. Redukcia nového vodopádu a leta práva. Zdroj: f. Zapata.

Nakoniec je výstup systému:

A (s) = x (s) ⋅g₁⋅ g₂ ⋅g₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅g₃ ⋅ g₄]

Odkazy

1. Alaydi, J. Ovládanie diagramu systémového bloku. Obnovené z: stránky.iugaza.Edu.$.
2. Bolton, W. 2006. Riadenie. Druhý. Vydanie. Alfa omega.
3. Cwalinsky, J. Úvod do systémového bloku Algebra. Získané z: cedengineering.com.
4. Dadachconnection. Schéma blokov. Získané z: Dadach.com.
5. Ogata, K. 2010. Moderné riadiace inžinierstvo. 5. Vydanie. Pearson.