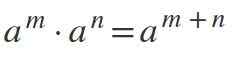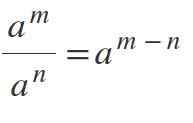Zákony exponentov

Aké sú zákony exponentov?

Ten Zákony exponentov Sú to tie, ktoré sa vzťahujú na toto číslo, ktoré naznačuje, koľkokrát sa musí základné číslo vynásobiť samo o sebe. Exponenti sú tiež známe ako právomoci. Potenciácia je matematická operácia tvorená základňou (a), exponentom (m) a výkonom (b), čo je výsledkom operácie.

Exponenty sa všeobecne používajú, keď sa používajú veľmi veľké množstvá, pretože to nie sú nič iné ako skratky, ktoré predstavujú násobenie toho istého čísla určité množstvo násobku. Exponenti môžu byť pozitívne aj negatívne.

Čo sú exponenti v matematických operáciách?

Ako je uvedené vyššie, exponenty sú skrátenou formou, ktorá predstavuje násobenie čísel pre seba, kde exponent sa týka iba ľavého čísla. Napríklad:

2³ = 2*2*2 = 8

V takom prípade je číslo 2 základom výkonu, ktorý sa vynásobí trikrát, ako je uvedené exponentom, ktorý sa nachádza v pravom hornom rohu základne. Existujú rôzne spôsoby čítania výrazu: 2 zvýšené na 3 alebo 2 zvýšené na kocku.

Exponenty tiež označujú počet, koľkokrát sa dá rozdeliť, a na odlíšenie tejto operácie od násobenia exponent nesie mínus (-) znamenie pred sebou (je záporný), čo znamená, že exponent je v menovateľovi menovateľa zlomok. Napríklad:

2^{- 4} = 1/2*2*2*2 = 1/16

To by sa nemalo zamieňať s prípadom, v ktorom je základňa záporná, pretože bude závisieť od toho, či je exponent rovnomerný alebo čudný, aby sa zistilo, či bude sila kladná alebo negatívna. Preto musíte:

- Ak je exponent rovnomerný, sila bude pozitívna. Napríklad:

(-7)² = -7 _* -7 = 49.

- Ak je exponent čudný, sila bude negatívna. Napríklad:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Existuje osobitný prípad, keď sa exponent rovná 0, sila sa rovná 1. Existuje tiež možnosť, že základňa je 0; V takom prípade bude v závislosti od exponentu neurčitý alebo nie.

Ak chcete vykonávať matematické operácie s exponentmi, je potrebné.

Aké sú zákony exponentov?

Prvý zákon: Výkon exponentov rovná sa 1

Ak je exponent 1, výsledok bude rovnaká hodnota ako základ: a¹ = a.

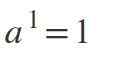
Príklady

9¹ = 9.

22¹ = 22.

895¹ = 895.

Druhý zákon: Výkon exponentov rovná sa 0

Ak je exponent 0, ak sa základňa líši od nuly, výsledkom bude: a⁰ = 1.

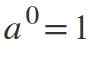
Príklady

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Tretí zákon: Negatívny exponent

Pretože exponent je negatívny, výsledkom bude zlomok, kde bude sila menovateľom. Napríklad, ak je m pozitívny, potom^-m = 1/a^m.

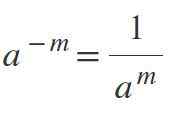
Príklady

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Štvrtý zákon: násobenie rovnakých právomocí ako rovnaké

Na vynásobenie sily, kde sú základy rovnaké a líšia sa od 0, je udržiavaná základňa a exponenty sa pridávajú: a^m _* doⁿ = a^m+n.    

Príklady

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^jedenásť

Piaty zákon: Divízia moci s rovnakou základňou

Na rozdelenie síl, v ktorých sú základy rovnaké a odlišné od 0, sa zachováva základňa a exponenty sa odpočítajú takto: a^m /ⁿ = a^M-n.    

Príklady

- 9² / 9¹ = 9 ^{(dvadsaťjeden)} = 9¹.

- 6^pätnásť / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Šiesty zákon: Násobenie rôznych právomocí s inou základňou

V tomto zákone je opak toho, čo je vyjadrené vo štvrtom; To znamená, že ak máte rôzne základne, ale s rovnakými exponentmi, základy sa vynásobia a exponent je udržiavaný: a^m _* b^m = (a_*b) ^m.

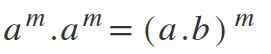
Príklady

- 10² _* dvadsať² = (10 _* dvadsať)² = 200².

- Štyri. Päť^jedenásť _* 9^jedenásť = (45*9)^{11 =} 405^jedenásť.

Ďalším spôsobom, ako reprezentovať tento zákon, je, keď je násobenie vysoké ako moc. Exponent teda bude patriť do každého z podmienok: (a_*b)^m= a^m_* b^m.

Príklady

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Siedmy zákon: rôzne divízie moci

Ak máte rôzne základne, ale s rovnakými exponentmi sú základy rozdelené a exponent je udržiavaný:^m / b^m = (a / b)^m.

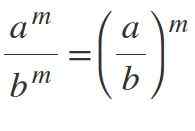
Príklady

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

Podobne, keď je rozdelenie vysoké pre moc, exponent bude patriť do každého z podmienok: (a / b) ^m = a^m /b^m.

Príklady

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Existuje prípad, keď je exponent negatívny. Takže, aby som bol pozitívny, hodnota čitateľa sa investuje s hodnotou menovateľa nasledovne:

- (A / b)^-n = (b / a)ⁿ = bⁿ /ⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Ôsmy zákon: Sila moci

Ak máte silu, ktorá je zvýšená na inú moc -to znamená, že dvaja exponenti súčasne -základňa sa udržiava a exponenty sa množia: (a^m)ⁿ= a^m*n.

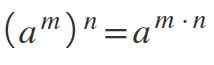
Príklady

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Deviaty zákon: frakčný exponent

Ak má výkon ako exponent frakcie, je to vyriešené jeho transformáciou na koreň N-ESIMA, kde čitateľ zostáva ako exponent a menovateľ predstavuje koreňový index:

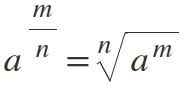
Príklad

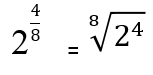
Vyriešené cvičenia

Cvičenie 1

Vypočítajte operácie medzi právomocami, ktoré majú rôzne základy:

2⁴ _* 4⁴ / 8².

Riešenie

Pri uplatňovaní pravidiel exponentov sa základy vynásobia v čitateľovi a zachováva sa exponent, ako je tento:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Teraz, keďže existujú rovnaké základne, ale s rôznymi exponentmi je základňa udržiavaná a exponenty sa odpočítajú:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Cvičenie 2

Vypočítajte operácie medzi vysokými silami na inú moc:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Riešenie

Pri uplatňovaní zákonov musíte:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Odkazy

1. Aponte, G. (1998). Základné základné matematické základy. Pearson Vzdelanie.
2. Corbalán, f. (1997). Matematika aplikovaná na každodenný život.
3. Jiménez, J. R. (2009). Matematika 1 september.
4. Max Peters, w. L. (1972). Algebra a trigonometria.
5. Rees, P. Klimatizovať. (1986). Reverzný.