Zákon Kirchhoff

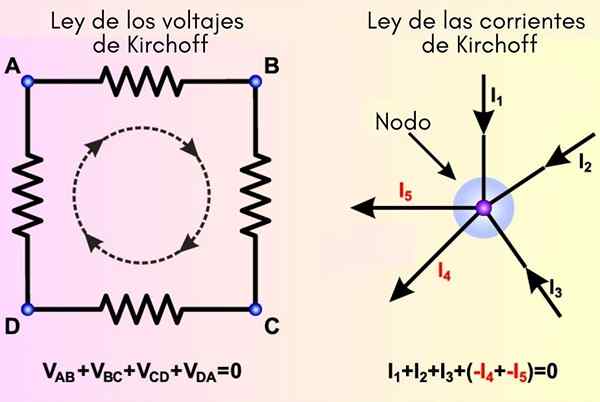
Kirchoffove zákony vyplývajú zo zásady energetiky a ochrany záťaže, respektíve. Vľavo je zákon o okázach zriadený a napravo prúdy

Aké sú Kirchoffove zákony?

Ten Kirchoff zákon Skladajú sa z uplatňovania zásady ochrany elektrického náboja a princípu ochrany energie na elektrické obvody, aby sa vyriešili tie, ktoré majú niekoľko oká.

Tieto pravidlá, pretože nie sú zákonmi v prísnom slova zmysle, sú spôsobené nemeckým fyzikom Gustavom Kirchoffom (1824-1887). Jeho použitie je nevyhnutné, keď Ohmov zákon nestačí na určenie napätia a prúdy v obvode.

Pred vyhlásením a uplatňovaním Kirchoffových zákonov je vhodné pamätať na význam niektorých dôležitých konceptov elektrických obvodov:

• Uzol: Union Bod medzi dvoma alebo viacerými vodivými vodičmi.
• Pobočka: Prvky obvodu, ktoré sú medzi dvoma po sebe idúcimi uzlami, cez ktoré cirkuluje ten istý prúd.
• Zaviazať: Trajektória alebo uzavretá slučka zložená z dvoch alebo viacerých vetiev, ktoré sa pohybujú rovnakým smerom, bez toho, aby prešli rovnakým bodom.

Kirchoffov prvý zákon

Je tiež známy ako zákon prúdov alebo pravidlá uzlov a uvádza to:

Súčet prúdov, ktoré vstupujú do uzla, sa rovná súčtu prúdov, ktoré z nej vychádzajú.

Takže matematickým spôsobom je prvý zákon vyjadrený ako:

∑ i = 0

Kde symbol σ označuje súčet.

Predchádzajúca rovnica ustanovuje, že keďže elektrický náboj nie je vytvorený alebo zničený, celý prúd (zaťaženie na jednotku času), ktorý vstupuje do uzla, sa musí rovnať tomu, ktorý z neho vychádza.

Môže vám slúžiť: umelé satelity

Príklad

Na pohodlné uplatnenie zákona o prúdoch je znamenie priradené k prichádzajúcim prúdom a opačným znakom k odchádzajúcim prúdom. Výber je úplne svojvoľný.

Nasledujúci obrázok zobrazuje dva prúdy, ktoré vstupujú do uzla, nakreslené v červenej farbe: i₁ a ja₂, a že pri odchode sú zobrazené zelenou farbou: prúdy i₃, Jo₄ a ja₅.

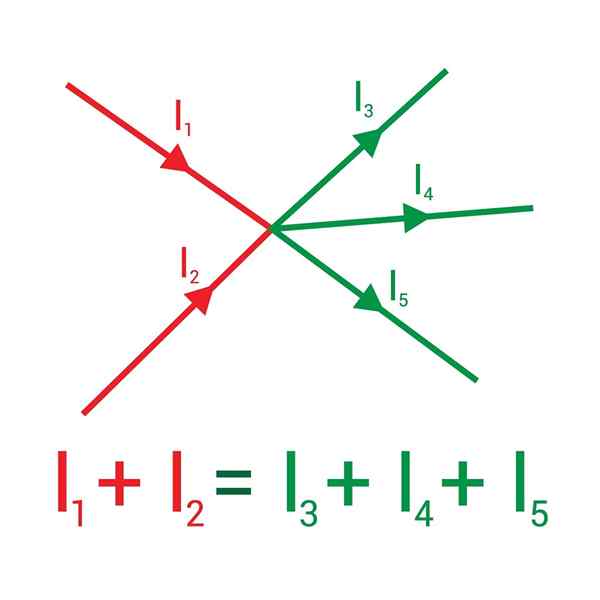Súčet prúdov, ktoré vstupujú do uzla, sa rovná súčtu prúdov, ktoré z nej vychádzajú

Priradenie znamenia (+) k prichádzajúcim prúdom a (-) k odchádzajúcemu prvému pravidlu Kirchoff sa ustanovuje:

Jo₁ + Jo₂ - Jo₃ - Jo₄ - Jo₅= 0 ⇒ i₁ + Jo₂ = I₃ + Jo₄ + Jo₅

Kirchoffov druhý zákon

Ďalšie mená Kirchoffovho druhého zákona sú: Zákon o napätí, Zákon o napätí ani zázrak. V každom prípade to ustanovuje:

Algebraický súčet napätia kvapky pozdĺž ôk sa rovná 0.

Toto je spôsob, ako uplatniť zachovanie energie v obvode, pretože napätie v každom prvku je zmena energie na jednotku zaťaženia.

Preto pri cestovaní po uzavretej časti (ôk) sa algebraický súčet napätia zvyšuje a pády je 0 a dá sa napísať:

∑ v = 0

Príklad

Na nasledujúcom čísle máte sieť Abcda, cez ktoré prúd cirkuluje v smere hodinových ihiel a trasy sa môže začať v ktoromkoľvek bode obvodu.

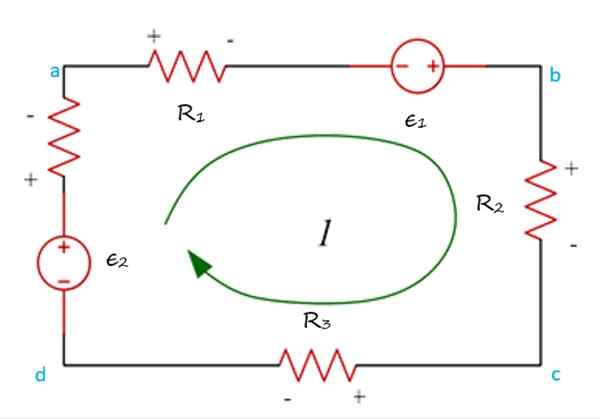Príklad ôk cestovaného v pláne, kde sa ukázalo, že zvýšenie a potenciálne pády uplatňujú zákon Kirchoff Tensions Law. Zdroj: f. Zapata.

Je to tiež potrebné. Zvyčajné je priradiť ako pozitívne zvýšenie napätia, to znamená, keď prúd cirkuluje od ( -) do (+). Potom je pokles napätia, ktorý sa vyskytuje, keď prúd prechádza z (+) na ( -), negatívny.

Môže vám slúžiť: oxid kremíka (SiO2): štruktúra, vlastnosti, použitia, získanie

Spustenie trasy siete v bode „A“ je odpor R₁. V ňom zaťaženia zažívajú potenciálnu kvapku, symbolizované znakmi (+) vľavo a ( -) nad odporom.

Preto napätie alebo napätie v R₁ Má negatívne znamenie.

Potom dosiahnete priamy zdroj napätia, ktorý sa nazýva ε₁, ktorého polarita je menšia (-) Viac (+). Tam elektrické náboje prechádzajú potenciálnym nárastom a tento zdroj sa považuje za pozitívny.

Podľa tohto postupu pre zostávajúci odpor a druhý zdroj sa v dôsledku toho získa nasledujúca rovnica:

−v₁ + ε₁ - Vložka₂ - Vložka₃ + ε₂ = 0

Kde v₁, Vložka₂ a v₃ sú napätia v odporoch r₁, R₂ a r₃. Tieto napätie nájdete zo zákona Ohm: v = i · r.

Cvičenie

Nájdite hodnotu prúdov i₁, Jo₂ a ja₃ znázornené na obrázku.

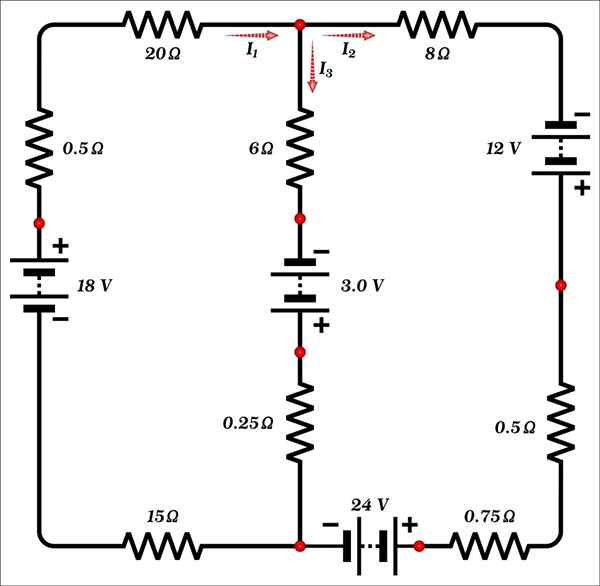
Riešenie

Tento obvod pozostáva iba z dvoch oká a má 3 neznáme: prúdy a₁, Jo₂ a ja₃, Takže na nájdenie riešenia sú potrebné najmenej 3 rovnice.

V uzle (bod označený červenou farbou), ktorá je v hornej časti obvodu na centrálnej vetve, je pozorované, že prúd i₁ je prichádzajúci, zatiaľ čo prúdy i₂ a ja₃ Odchádzajú.

Zákon Kirchoff Currents preto vedie k prvej rovnici:

1) i₁ - i₂ - i₃ = 0

Spodný uzol poskytuje rovnaké informácie, preto ďalším krokom je cestovanie po okázach.

Prvá sieť

Na stanovenie nasledujúcej rovnice sa sieť vľavo prechádza v rozvrhu, počnúc ľavým horným rohom. To je zmysel, v ktorom cirkulujú prúdy a prúdy₁ a ja₃.

Môže vám slúžiť: optický komparátor: Na čo je to a časti

Poznač si to:

• Jo₁ prechádza odpormi 20 Ω, 15 Ω a 0.5 Ω a 18 V batéria, kde prežíva potenciálny vzostup.
• Z toho, ja₃ Prechádza odporom centrálnej vetvy 6 Ω a 0.15 Ω a na 3 batériu.0 V je potenciálny nárast.

Podobne sa zákon OHM V = i ∙ r používa na stanovenie napätia v každom odporu podľa tohto:

-20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Objednávanie podmienok:

(−20 −15 - 0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

-35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Druhá sieť

Tretia rovnica sa získa cestovaním po okolí vpravo, začínajúc v uzle hornej časti obvodu. Zistilo sa, že:

• Jo₂ Prejdite si odpor 8 Ω, 0.5 Ω a 0.75 Ω, plus batérie 12 V a 24 V. Podľa polarity batérií na trase dochádza k nárastu potenciálu v 12 V a pokles v 24 V.
• Dôležité: Prehliadka druhej siete (v pláne) je proti I₃, Preto napätie v odporoch 6 Ω a 0.25 Ω sú potenciálne stúpanie a nesie pozitívne znamenie. Podľa polarity batérií došlo.

S tým všetkým dosiahnete:

-8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Súčasná výpočet

Rovnice 1), 2) a 3) Vytvorte systém 3 lineárnych rovníc s 3 neznámymi, ktorých riešenie je:

Jo₁ = 0.381 a; Jo₂ = -0.814 a; Jo₃ = 1.195 a

Záporné znamenie v prúdu i₂ znamená, že tečie opačným smerom systému.