Kepler zákony vysvetlenie, cvičenia, experiment

Ten Kepler zákony O planétovom hnutí bolo formulované nemeckým astronómom Johannesom Keplerom (1571-1630). Kepler ich odvodil na základe práce svojho učiteľa dánskeho astronóma Tycha Brahe (1546-1601).

Brahe starostlivo zostavil údaje z planétových pohybov viac ako 20 rokov, s prekvapivou presnosťou a presnosťou, ak sa vezme do úvahy, že v čase, keď sa ďalekohľad ešte nevymyslel. Platnosť vašich údajov je dodnes platná.

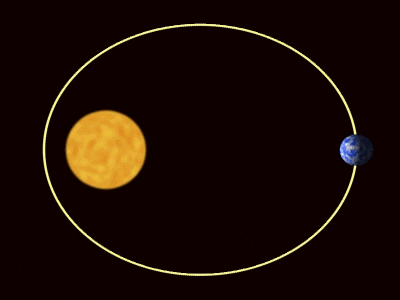postava 1. Obežné dráhy planét podľa Keplerových zákonov. Zdroj: Wikimedia Commons. Willow/CC od (https: // creativeCommons.Org/licencie/o/3.0)

[TOC]

Keplerove 3 zákony

Keplerove zákony stanovujú:

-Prvá zákona: Všetky planéty opisujú eliptické obežné dráhy so slnkom v jednom z bodov.

-Druhý zákon alebo zákon: Čiara nasmerovaná zo slnka na akúkoľvek planétu (ohniskové rádio), zametajte rovnaké oblasti v rovnakých časoch.

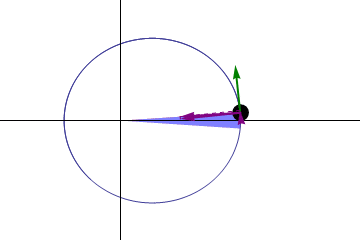Obrázok 2. Zákon. Zdroj: Wikimedia Commons. Gonfer/cc By-SA (https: // creativecommons.Org/licencie/By-SA/3.0)

-Tretí zákon: Štvorec času, ktorý berie akúkoľvek orbitál planéty okolo slnka, je úmerný kocky svojej priemernej vzdialenosti od slnka.

Byť Tón povedal čas, nazvaný Orbitálne obdobie, a r Priemerná vzdialenosť, potom:

Tón² je úmerný R³

T = k r³

To znamená, že kvocient Tón²/ r³ Je to rovnaké pre všetky planéty, ktoré umožňuje vypočítať orbitálny polomer, ak je známe orbitálne obdobie.

Kedy Tón Je vyjadrená v rokoch a r V astronomických jednotkách UA*, proporcionálnu konštantu stojí za k = 1:

Tón²= r³

*Astronomická jednotka je rovnocenná s 150 miliónmi kilometrov, čo je priemerná vzdialenosť medzi zemou a slnkom. Orbitálne obdobie Zeme je 1 rok.

Univerzálny zákon o gravitácii a Keplerov tretí zákon

Zákon o univerzálnej gravitácii ustanovuje, že veľkosť gravitačnej príťažlivej sily medzi dvoma masovými objektmi M a m ktorých, ktorých centrá sú oddelené vzdialenosti r, Je daný:

F = g mm /r²

G je univerzálna gravitačná konštanta a jej hodnota je g = 6.674 x 10 ^-jedenásť N.m²/kg² .

Teraz sú obežné dráhy planét eliptické s veľmi malou excentricitou.

To znamená, že obežná dráha sa príliš nepohybuje od kruhu, s výnimkou niektorých prípadov, ako je napríklad trpaslík pluto. Ak priblížime obežné dráhy k kruhovej forme, zrýchlenie pohybu planéty je:

do_c = v²/r

Vzhľad F = ma, mať:

G mm /r² = m.vložka²/r

Tu vložka Je to lineárna rýchlosť planéty okolo slnka, statický a hmotný predpoklad M, zatiaľ čo planéta je m. Tak:

Môže vám slúžiť: Významné čísla: Pravidlá, príklady, vyriešené cvičenia

To vysvetľuje, že planéty najvzdialenejšie od slnka majú nižšiu orbitálnu rýchlosť, pretože závisí od toho 1/√r.

Pretože vzdialenosť, ktorú planéta prechádza, je približne dĺžka obvodu: L = 2πr a trvá rovnaký čas t, orbitálnu periódu, získa sa:

V = 2πr /t

Vyrovnanie oboch výrazov pre v A Platný výraz pre t sa získava², Štvorec orbitálneho obdobia:

A to je presne Keplerov tretí zákon, pretože v tomto výraze zátvorky 4π² Gm Je to preto konštantné Tón² je úmerný vzdialenosti r povýšený na kocku.

Definitívna rovnica pre orbitálne obdobie sa získa extrahovaním druhej odmocniny:

Výpočet hmotnosti slnka

Koľko stojí množstvo slnka? Je možné zistiť prostredníctvom tejto rovnice. Vieme, že orbitálne obdobie Zeme je jeden rok a orbitálny polomer je 1 UA, čo zodpovedá 150 miliónom kilometrov, takže máme všetky potrebné údaje.

V našej predchádzajúcej rovnici vyčistíme M, ale nie pred prevedením všetkých hodnôt na medzinárodný systém jednotiek, ak:

1 rok = 3.16 x 10⁷ sekundy.

1 UA = 150 miliónov km = 1.5 x10^jedenásť m.

A nahradením údajov v rovnici získame pomerne úspešný odhad slnka Slnka v 2.0 x 10 ³⁰ kg.

Cvičenia

Aj keď Kepler mal na mysli iba planéty, keď odvodil svoje slávne zákony, sú platné aj pre pohyb satelitov a ďalšie telá slnečnej sústavy, ako uvidíme ďalej.

- Cvičenie 1

S vedomím, že Jupiterova obežná dráha je 5.19 -krát väčší ako obdobie Zeme, nájdite orbitálne obdobie Jupitera.

Riešenie

Podľa definície astronomickej jednotky je Jupiter zo Slnka 5.19 UA, preto podľa Keplerovho tretieho zákona:

Tón²= r³= (5.19)³ roky

Preto T = (5,19)^3/2  Roky = 11.8 rokov

- Cvičenie 2

Halley Comet navštevuje slnko každých 75.3 roky. Nájsť:

a) Hlavné polopriepustenie jeho obežnej dráhy.

b) miera apeliu, ak perihelium meria 0.568 UA.

Riešenie

Halley Comet navštevuje slnko každých 75.3 roky. Nájsť:

a) Hlavné polopriepustenie jeho obežnej dráhy.

b) miera apeliu, ak perihelium meria 0.568 UA.

Roztok

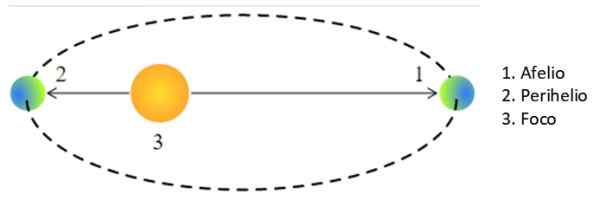
Keď je planéta alebo iná hviezda v bode najbližšie k slnku, hovorí sa, že je v perihelio, A keď je ďalej, v afovanie. V osobitnom prípade kruhovej obežnej dráhy je R v Keplerovom treťom zákone polomerom obežnej dráhy.

Môže vám slúžiť: Antoínové konštanty: vzorce, rovnice, príklady

Avšak na eliptickej obežnej dráhe je nebeské telo viac -menej od slnka, čo je semi -major „a“ priemer medzi Aprotess a perihelium:

Obrázok 3. Aflio a Perihelio. Zdroj: Wikimedia Commons. Pearson Scott Foresman / verejná doména

Preto nahradíme R v Keplerovom treťom zákone, ktorý má za následok Halley v:

Tón²= a³→ A = (t)²³ → A = (75.3) ²³ Ua = 17.832 UA

Riešenie B

A = ½ (perihelio + Apelio)

17.832 = ½ (0.568+ AFLIO) → AFLIO = 2 x 17.832 - 0.568 UA = 35.10 ua.

Experimentovať

Analyzujte pohyb planét vyžaduje týždne, mesiace a dokonca roky starostlivého pozorovania a registrácie. Ale v laboratóriu je možné vykonať veľmi jednoduchý experiment, aby sa dokázal, že zákon Keplerovho rovného je splnený.

Na tento účel je potrebný fyzický systém, v ktorom je sila, ktorá riadi hnutie. Takýto systém pozostáva z hmoty zviazanej na dlhé lano, s druhým koncom pevného vlákna na podporu.

Cesto oddeľuje malý uhol rovnovážnej polohy a je vytlačené miernym impulzom, takže vykonáva oválny (takmer eliptický) pohyb na horizontálnej rovine, akoby to bola planéta okolo slnka.

Na krivke opísanej kyvadlom môžeme dokázať, že zametá rovnaké oblasti v rovnakých časoch, áno:

-Uvažujeme o vektorových rádiách od stredu príťažlivosti (počiatočný rovnovážny bod) po polohu hmotnosti.

-A my barmos medzi dvoma po sebe idúcimi momentmi rovnakého trvania, v dvoch rôznych oblastiach pohybu.

Čím dlhšie sú kyvadlové vlákno a nižšie uhol, ktorý sa odchyľuje od vertikálu, bude čistá restoratívna sila horizontálnejšia a simulácia sa podobá prípadu pohybu centrálnou silou v rovine.

Potom sa opísaný oválny prístup k elipse, ako je tá, ktorú planéty cestujú.

Materiál

-Nemenné vlákno

-1 cesto alebo kovová guľa natretá biela, ktorá pôsobí ako šošovica kyvadla

-Vládca

-Dopravník

-Picture Camera s automatickým bleskovým diskom

-Podpora

-Dva zdroje osvetlenia

-List papiera alebo čiernej lepenky

Môže vám slúžiť: Veľká teória kríz: História, princípy, údaje pre a proti

Postup

Zostava čísla je potrebná na fotografovanie viacerých zábleskov kyvadla podľa jeho trajektórie nasleduje. Aby ste to dosiahli, musíte vložiť fotoaparát tesne nad kyvadlo a automatický strobe album pred objektívom.

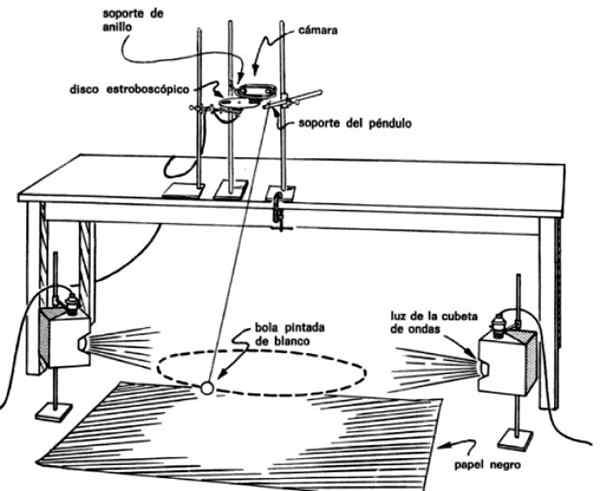Obrázok 4. Zostava kyvadla na overenie, či zametá rovnaké oblasti v rovnakých časoch. Zdroj: Laboratórna príručka PSSC.

Týmto spôsobom sa obrázky získajú v pravidelných časových intervaloch kyvadla, napríklad každých 0.1 alebo každé 0.2 sekundy, ktoré umožňujú poznať čas potrebný na presun z jedného bodu na druhý.

Musíte tiež pohodlne osvetľovať hmotnosť kyvadla a umiestniť svetlá na obidve strany. Šošovka musí byť natretá biela, aby sa zlepšil kontrast na pozadí, ktorý pozostáva z rozšíreného čierneho papiera na zemi.

Teraz musíte skontrolovať, či kyvadlo zametá rovnaké oblasti v rovnakých časoch. Z tohto dôvodu je vybraný časový interval a body, ktoré zaberá kyvadlo v uvedenom intervale.

Na obrázku je čiara nakreslená zo stredu oválu do týchto bodov, a preto budeme mať prvú z oblastí zametaných kyvadlom, čo je približne eliptický sektor, ako je ten, ktorý je uvedený nižšie:

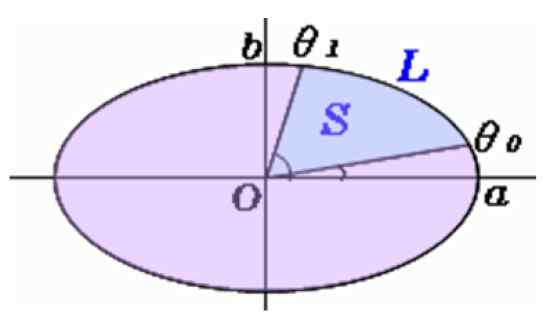Obrázok 5. Oblasť eliptického sektora. Zdroj: f. Zapata.

Výpočet oblasti eliptickej sekcie

Uhly sa merajú pomocou dopravníka θ_ani a θ₁, A tento vzorec sa používa na nájdenie S, oblasť eliptického sektora:

S = f (9₁) - f (9_ani)

S F (9) daná:

Poznač si to do a b Sú to polo -senije väčšie a menšie. Čitateľ by sa mal starať iba o starostlivo zmerať polo -mens a uhly, pretože existujú online kalkulačky na ľahké vyhodnotenie tohto výrazu.

Ak však trváte na tom, aby ste výpočet robili ručne, musíte si uvedomiť, že uhol 9 sa meria v stupňoch, ale v čase zadávania údajov do kalkulačky sa musia hodnoty vyjadriť v radiánoch.

Potom musíte označiť ďalšiu dvojicu bodov, do ktorých kyvadlo investovalo v rovnakom časovom intervale, a nakresliť zodpovedajúcu oblasť, čím sa vypočítava jeho hodnota s rovnakým postupom.

Overenie zákona rovnakých oblastí

Nakoniec zostáva overiť, či je zákon oblastí splnený, to znamená, že v rovnakých časoch sú rovnaké oblasti zametané.

Výsledky sa trochu odchýli od toho, čo očakávalo? Musíte mať na pamäti, že všetky opatrenia sú sprevádzané ich experimentálnou chybou.

Odkazy

1. Kalkulačka online Keisan. Plocha kalkulačky eliptického sektora. Získané z: Keisan.Kasio.com.
2. Opentax. Keplerov zákon o planetárnom návrhu. Zdroj: Openstax.orgán.
3. Pssc. Laboratórna fyzika. Redaktor sa vrátil. Získané z: Knihy.Riadenie.co.
4. Palen, s. 2002. Astronómia. Séria Schaum. McGraw Hill.
5. Pérez r. Jednoduchý systém s centrálnou silou. Získané z: Francesphysics.Blog.com
6. Stern, D. Tri Keplerov zákony planétového hnutia. Získané z: Phy6.orgán.