De Morgan zákony

Vysvetlíme, aké sú Morganove zákony, demonštrujeme ich a uvádzame príklady

postava 1.- Matematik Augustus z Morganu (1806-1871) a jeho zákony o návrhu logiky. Zdroj: f. Zapata.

Aké sú zákony De Morgan?

Zákony spoločnosti De Morgan sú dva logické zákony patriace k návrhovej logike, ktorú formuloval anglický matematik Augustus z Morgan (1806-1871). Zistia nasledujúce, pokiaľ ide o zloženú logickú ponuku:

1. Opak spojenia je rovnocenný s disjunkciou, ktorý sa tvorí s protikladmi alebo popieraním návrhov, ktoré tvoria spojenie.
2. Popieranie disjunkcie možno vyjadriť ako spojenie zložené z protikladov alebo popierania návrhov zapojených do disjunkcie.

V zápise logiky propozície sú zákony De Morgan vyjadrené kompaktným a formálnejším spôsobom, ako je tento:

1. ∼ (p ∧ q) ⇔ ∼p ∨q
2. ∼ (p ∨ q) ⇔ ∼p ∧q

To, čo tieto zákony vyjadrujú, je to, že buď pri odmietnutí spojenia alebo disjunkcie je výsledok rovnocenný s odopaním každého zo zúčastnených návrhov osobitne a investovať konektor, ktorý ich spája.

Pre lepšie pochopenie zákonov De Morgana je potrebné preskúmať význam návrhov a symbolov používaných v návrhu logiky, aby ste zistili, ako sa tieto zákony pohodlne uplatňujú.

Logický zápis

Základným nástrojom návrhu logiky sú návrhy. Logický návrh je vyhlásenie, ktoré pripúšťa a skutočná hodnota, Či je to pravda alebo nepravdivé, ale nie oboje súčasne. V tomto nie je povolená žiadna nejednoznačnosť, to znamená, že niet pochýb.

Návrh je označený malými písmenami, ako v nasledujúcich príkladoch:

• Otázka: Mexico City je hlavným mestom Mexika (True).
• Otázka: Získa sa 2 a 3, 4 (nepravdivé).
• Odpoveď: Všetky cicavce sú pozemné zvieratá (nepravdivé).

Môže vám slúžiť: Heptagon

Existujú tiež zložitejšie návrhy, ktoré sú štruktúrované pomocou jednoduchých návrhov, ako sú tieto:

• Otázka: Carlos pôjde do kina, ak neprší.
• Otázka: Ana je chemik alebo morský biológ.
• Odpoveď: Juan ide na večeru alebo Pedro uvidí hru v televízii.

Logické konektory

Logické konektory sú symboly používané na prepojenie jednoduchých návrhov, a tak vytvára zložitejšie návrhy. V logike návrhu má každý z nich osobitný význam.

Najpoužívanejšími konektormi sú spojenie, disjunkcia, výhradné disjunkcie, odmietnutie, podmieneniu a bipodvojenosť.

Spojenie

Spojenie je označené invertovaným písmenom „V“. Zložená ponuka prostredníctvom spojenia je symbolizovaná P ∧ Q, takto:

• P ∧ Q: Mexico City je hlavným mestom Mexika a je v Severnej Amerike.

Je ľahké tu identifikovať, že P je „Mexico City je hlavným mestom Mexika“ a Q je „v Severnej Amerike“.

Disjunkcia

Rozlišujú sa dva typy disjunkcie: slabé a exkluzívne. A slabý disjunkcia Je symbolizovaný ∨ a v logickom zápise by to bolo p ∨ q. Príklad tohto druhu disjunkcie je:

• P ∨ Q: Juan je futbalista alebo Juan je tenista.

Namiesto toho exkluzívny disjunkcia Symbolizuje to znamením ⊻ a naznačuje, že jeden z návrhov je potrebné vylúčiť napríklad:

P ⊻ Q: Alicia má 20 rokov alebo Alicia má 22 rokov.

Rozdiel medzi oboma typmi je jasný, v exkluzívnom disjunkcii je vylúčený jeden z návrhov, pretože ak má Alicia 20 rokov, nemôže byť 22 a naopak. Na druhej strane, v slabom disjunkcii, Juan môže byť futbalista a tenistický hráč súčasne.

Odmietavý postoj

Uvedením symbolu ∼ a návrh je to odopreté, ako v:

• Otázka: ∼ (Veracruz je hlavným mestom Mexika).

To sa číta ako „Veracruz nie je hlavným mestom Mexika“. Ďalšími spôsobmi vyjadrenia popierania, okrem „nie“, sú frázy ako „je nepravdivé“, „Je to lož, ktorá“ a „nie je pravda“.

Môže vám slúžiť: lineárna interpolácia

Podmienenosť

Sú to kompozitné návrhy, ktoré zvyčajne používajú slová „áno“ a „potom ...“ na prepojenie dvoch návrhov, v ktorých existuje podmienenosť alebo dôsledok. Časť návrhu, ktorý je napísaný bezprostredne po „áno“, je predchádzajúci mávať hypotéza návrhu a čo je po termíne „potom“, je záver ani v dôsledku.

Symbol používaný pre podmieneniu je šípka zľava doprava „→“, preto je podmienenosť medzi dvoma návrhmi znázornená ako p → q, ktoré je možné čítať ako „ak p, potom q“. Napríklad:

P → Q: Ak prší popoludní, nebudem hrať tenis.

Obojstrannosť

V tomto type návrhu sa používa fráza „áno a iba ak“ na spojenie dvoch návrhov, nazývaných prvá a druhá dvojstranná členka. Použitý symbol je obojsmerná šípka „↔“.

Tieto dva návrhy spojené „áno a iba ak“ sa nazývajú najprv a druhý člen a obojstrannosť dvoch návrhov P a Q zostáva ako p ↔ q. Napríklad:

P ↔ Q: Maria rád jazdí na bicykli, ak a iba vtedy, ak je deň slnečný.

Demonštrácia zákonov De Morgan

Zákony de Morgan sú súčasťou logických rovnocenností a môžu sa demonštrovať prostredníctvom tabuliek pravdy, ktoré sa používajú na poznanie pravdy (pravej alebo nepravdivej) hodnoty návrhu.

Pretože spojenie platí iba vtedy, keď sú P a Q pravdivé, jeho tabuľka pravdy je:

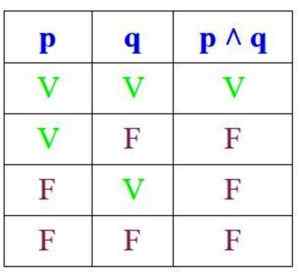
Na druhej strane, v disjunkcii je návrh pravdivý, ak sú P a Q pravdivé alebo ak aspoň jeden z nich je, ale je nepravdivé, ak sú obidve:

Môže vám slúžiť: Permutácie bez opakovania: vzorce, demonštrácia, cvičenia, príklady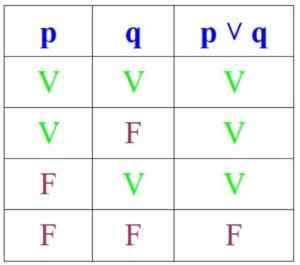

Teraz popieranie premení pravdu na falošnú a naopak. V tomto prípade sú hodnoty pravdy ∼ (p ∧ q) a ∼ (p ∨ q) opakom hodnoty pravdy (p ∧ q) a (p ∨ q):

A musí sa overiť, že tieto výsledky sa získajú pri vykonávaní príslušných tabuliek pravdy (∼ P ˅ ∼ Q) a (∼ P ˄ ∼ Q):

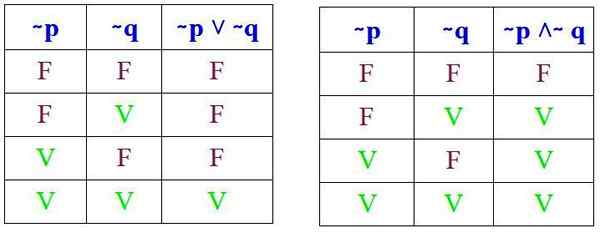
A skutočne, pri porovnaní príslušných tabuliek pravdy sa zistí, že zákony De Morgan sú splnené. Teraz sa zobrazia dva príklady jej uplatňovania.

Vyriešený príklad 1

Aplikujte zákony de Morgan na nájdenie ekvivalentnej expresie: ∼ (∼p ˅ ∼q)

• Riešenie

Daný expresia sa porovnáva ∼ (∼p ˅ ~ q) s Morganovým zákonom:

∼ (p ∨ q) ⇔ ∼p ∧q

A zistilo sa, že odmietnutie je už mimo zátvorky v oboch prípadoch, preto sa dodržiavajú pokyny zákona: odmieta ∼p, popiera ∼q a konektor sa zmení:

∼ (∼p ˅ ∼q) ⇔ ∼ (∼p) ∧ ∼ (∼q) ⇔ p ∧ q

Vyriešený príklad 2

Stanovte ekvivalentnú expresiu ∼ [∼p ˄ ∼ (∼q)] ≡

• Riešenie

Po prvé, zamietnutie ∼q je zjednodušený:

∼ [∼p ˄ ∼ (∼q)] ⇔ ∼ [∼p ˄ Q]

Pretože už existuje popieranie mimo zátvorky, výsledná expresia sa porovnáva s Morganovým zákonom: ∼ (p ∧ q) ⇔ ∼p ∨q

Ak chcete vyriešiť ∼ [∼p ˄ q], musíte poprieť ∼p, poprieť Q a zmeniť konektor:

∼ [∼p ˄ q] ⇔ (∼p) ∨ ∼q ⇔ p ˅ ∼q

Odkazy

1. Becerra, J.M.  UNAM LOGICKÉ POZNÁMKY.
2. Brilantný. Z Morganových zákonov. Zotavené z: brilantného.orgán.
3. Elektronické návody. Morganova veta. Obnovené z: elektroniky Tormales.WS.
4. López, f. Úvod do matematickej logiky. Obnovené z: YouTube.com
5. Muñoz, C. Úvod do logiky. Zdroj: webové stránky.Ucm.je.