Podpisuje zákon

- 3911
- 1045
- Gabriel Bahna
Vysvetlíme zákon znakov, s vyriešenými príkladmi a cvičeniami
 Schéma zákona o znakoch
Schéma zákona o znakoch Aký je zákon znakov?
Ten Podpisuje zákon Je to súbor pravidiel použitých v aritmetických a algebraických výpočtoch so skutočnými číslami na správne priradenie značky k výsledku, keď sú zapojené kladné aj záporné sumy.
Podľa operácie, ktorá sa vykonáva, existujú primerané pravidlá: súčet, odčítanie, násobenie a delenie, ktoré sú najzákladnejšie, a existujú aj pravidlá týkajúce sa potenciálnych a registračných operácií.
V danej operácii, či už ručne alebo s kalkulačkou, je potrebné správne uplatniť zákon o príznakoch, aby sa zaistil správny výsledok, pretože iba malá zmena v príznakoch výrazne mení sumy.
Zákon znakov pre každú základnú aritmetickú operáciu a prípady, ktoré sa môžu vyskytnúť.
Zákon o znakoch sumy
1) Ak majú čísla, ktoré sa majú pridať, rovnaké znamenie
Čísla sa pridávajú ako obvykle a výsledok sa pridá k znameniu čísel, bez ohľadu na to, či je to kladné alebo negatívne.
Je dôležité mať na pamäti, že pozitívne čísla zvyčajne nie sú pred znamením, ale sú napísané priamo. Na druhej strane, záporné čísla sú napísané v zátvorkách, najmä ak im predchádza symbol aritmetickej operácie, aby sa predišlo zmätku.
Príklady sumy čísel s rovnakým znakom:
3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21
2) Ak majú čísla, ktoré sa majú pridať
Čísla sa odpočítajú a k výsledku sa pridáva znak čísla, ktoré má najväčšiu absolútnu hodnotu, či už pozitívne alebo negatívne.
Ako príklad vykonávate operáciu 5 + (−14). Pretože absolútna hodnota (-14) je vyššia ako absolútna hodnota 5, 5 sa odpočítava od 14, čo dáva 9 a tento výsledok je umiestnený záporný znak:
Môže vám slúžiť: hranoly a pyramídy5 + (−14) = −9
Viac príkladov tohto pravidla uplatňované na súčet dvoch čísel rôznych znakov sú:
(−27) + 12 = −15
12 + (−7) = 5
Ak v operácii existuje viac ako dva prírastky s rôznymi znakmi, Asociatívny majetok sumy:
(-20) + 9 + (−7) = [(−20) + 9] + (−7)
Operácia sa prvýkrát vykonáva v Pracete, ktorá pozostáva zo súčtu dvoch čísel rôznych znakov, pre ktoré sa uplatňuje opísané pravidlo: výsledok sa odpočíta a znak čísla s najvyššou absolútnou hodnotou:
(−20) + 9 = −11
Operácia je taká:
(-20) + 9 + (−7) = (−11) + (−7)
Teraz máte súčet dvoch čísel toho istého znaku, potom sa zvyčajne pridávajú a výsledok je umiestnený záporným znakom:
(−20) + 9 + (−7) = (−11) + (−7) = −18
Znaky v náhradníkov
Odčítanie dvoch čísel je definované ako súčet opakovania. Naopak, opak ako číslo je uvedené číslo so zmeneným znakom. Napríklad opak 2 je (-2), opak (-5) je 5 a tak ďalej.
S týmto vedomím, keď máte odčítanie dvoch čísel:
A - B
Jednoducho sa zmení na súčet opak B:
A + ( - B)
A postupujte tak, ako je to opísané v predchádzajúcej časti. Poznámka na uvedenie znamenia + záporné číslo ho nemení, ale veľmi opatrné, opak nie je pravdivý.
Ak je číslo „A“, ktoré je Minuend, väčšie ako číslo „B“, ktoré je ukradnuté, funguje ako pri odčítaní prírodných čísel. Žiadny problém, pretože veľké množstvo sa odpočíta od menšej sumy:
Môže vám slúžiť: Nerovnosť trojuholníka: demonštrácia, príklady, vyriešené cvičenia25 - 8 = 17
S nasledujúcimi príkladmi je metóda pridania opak na odpočítanie veľmi pohodlná:
(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55
Zákon o znakoch v množení
Týmto spôsobom sa uplatňuje zákon znakov v násobení:
- Vynásobením dvoch čísel toho istého znaku je výsledok vždy pozitívny.
- Produkt dvoch opačných čísel znakov je vždy negatívny.
Zhrnutie pravidla znakov pre násobenie je uvedené na obrázku:
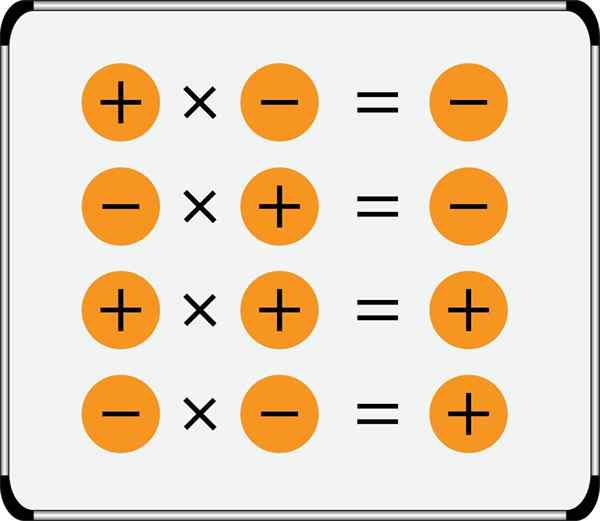
Všimnite si, že kladné čísla je možné písať bez predchádzajúceho znamenia, ale záporné čísla to vždy majú, okrem toho sa navyše navzájom napíšu dva aritmetické symboly, musia byť vždy oddelené zátvorkou:
Nesprávne: 3 × −4
Správne: 3 × (−4) = −12
(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270
Na vynásobenie viac ako dvoch čísel sa používa asociatívna vlastnosť násobenia, pretože poradie faktorov nemení produkt, napríklad pri vykonávaní:
(−2) × (−14) × 16
Môžete vynásobiť prvé dva faktory alebo posledné dva, ak chcete, a potom vynásobte výsledok zostávajúcim faktorom. V tomto prípade sa tieto dva faktory vynásobia najskôr začínajúc vľavo:
[(−2) × (−14)] × 16
Produkt dvoch záporných čísel je kladný, potom (-2) × (−14) = 28 a zostáva:
28 × 16 = 448
Zákon o znakoch v divízii
Je to analogické pravidlu príznakov pre násobenie:
- Pomer dvoch čísel toho istého znaku je vždy pozitívny.
- Rozdelením dvoch inak znakových čísel je výsledok vždy negatívny.
Napríklad:
24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36
Zákon o znakoch v posilňovaní a podaní
Písomný exponent čísla je:
don
Kde „A“ je základňou a „n“ je exponent. Podľa parity exponentov sa rozlišujú dva prípady:
Prípad 1: A je pozitívny
Ak je základňa pozitívna, výsledok je pozitívny bez ohľadu na to, či je exponent párny alebo čudný, ako v:
23 = 8
34 = 81
Prípad 2: A je negatívny
Tu sú dva prípady:
- Keď je exponent rovnomerný, výsledok je pozitívny.
- Ak je exponent čudný, je negatívny.
Príklady
32 = 3 ∙ 3 = 9
23 = 2 ∙ 2 ∙ 2 = 8
(−2)4 = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)3 = (−3) ∙ (−3) ∙ (−3) = −27
Operácie so zoskupujúcimi symbolmi
Často sa objavujú samostatné operácie so zoskupujúcimi symbolmi: zátvorky, zátvorky a kľúče. Sú vylúčené zvnútra von, berúc do úvahy nasledujúce:
- Ak symbolu zoskupenia predchádza kladné znamenie, môže sa odstrániť bez zmeny znakov obsahu, napríklad: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
- Ak negatívny znak predchádza skupinovému symbolu, je stiahnutý investovaním známky obsahu, napríklad: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
- Ak existujú kombinované operácie súčtu, odčítania, násobenia a rozdelenia, asociatívne a distribučné vlastnosti sa môžu použiť na pohodlie.
Vyriešené cvičenia
a) 10 + 10
Riešenie: 20
b) (-8) + (-3)
Riešenie: -11
c) (3) + (-10)
Riešenie: -7
d) (5) x (-3)
Riešenie: -15
e) (-10) x (-10)
Riešenie: 100
f) (18) ÷ (-3)
Riešenie: -6
G) (-10) ÷ (-2)
Riešenie: 5
h) 4 - ( - 7 + 9)
Riešenie: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11- 9 = 2

