Chémia

Zákon viacerých rozmerov

Zákon viacerých rozmerov

Aký je zákon viacerých rozmerov?

Ten Zákon viacerých rozmerov Uvádza sa, že ak sa dva prvky tvoria viac ako jedna zlúčenina, keď reagujú na seba, potom podiel hmotností, s ktorými je jedna z nich kombinovaná s pevnou hmotnosťou druhej, je to rovná vzťahu malých počtov.

Vyhlásenie zákona sa môže zdať zložité, ak nemáte k dispozícii príklad. Zvážte preto niektoré sušienky Oreos, ktoré sa skladajú z dvoch čokoládových viečok a pruhu sladkej smotany: T2C (t = veko a c = krém). Keby sme chceli vymyslieť robustnejší cookie Oreo, pridali by sme ďalší prúžok smotany, aby sme mali dvojitú smotanu (t2C2 alebo TC).

V dezertoch, ako sú napríklad Cookies Oreos. Zdroj: Brokensphere, CC BY-SA 3.0 https: // creativeCommons.Org/licencie/By-SA/3.0 cez Wikimedia Commons

Mohli by sme tiež pridať ďalší, takže cookie má trikrát viac krému ako konvenčný cookie (t2C3). Čo keby sme vložili ďalšie čokoládové veko do stredu bielych pruhov (t3C2)? Možnosti sú neobmedzené; Ale vždy pridávame veko alebo smotanovú jednotku. Nemyslíme si na polovicu veka (1/2 T) alebo pätinu smotany (1/5 ° C), pretože by to bolo nevhodné.

Rovnakým spôsobom sa to stáva s chemickými prvkami: ich atómy sa nerozdeľujú do zlúčenín. Preto masy T alebo C medzi ich zlúčeninami „vždy“ jednoduchý vzťah.

Vysvetlenie

Proporcie

Zákon viacerých rozmerov spolu so zákonom definovaných rozmerov predchádzal stechiometriu a prvé chemické vzorce. Zabudnime na cookies, ale nechajme si ich symboly: T a C. Prostredníctvom experimentov sa zistí, že prvky T a C tvoria niekoľko zlúčenín: t2C, TC a T2C3.

Pred chemickými receptúrami nebolo možné vedieť naraz, ktoré boli proporcie hmotnosti T a C v takýchto zlúčeninách. Musel ich najprv určiť. V zlúčenine sa zistilo, že hmotnosť T sa zdvojnásobila na hmotu C; Povedzme, 2 gramy T sa kombinujú s 1 gramom C.

Môže vám slúžiť: kapacita: jednotky, vzorce, výpočet, príklady

Potom sa v druhej zlúčenine museli hmotnosť T a C porovnať: 2 gramy T sú teraz kombinované s 2 gramami C. Vyskytuje sa tu otázka: Čo ak T a C môžu stále tvoriť ďalšiu zlúčeninu? Ak áno, určite by sa vytvorilo s 2 gramami T, ale tentoraz by sa kombinovali s 3 gramami C (1 gram + 1 gram + 1 gram).

Jednoduché masové vzťahy

Proporcie hmotností, s ktorými reagujú t a c, umožňujú stanoviť svoje chemické vzorce: t2C (2 gramy t: 1 gram c), TC (2 gramy t: 2 gramy c) a t2C3 (2 gramy t: 3 gramy c). Ak chceme porovnávať vzťahy hmotností T alebo C v týchto zlúčeninách, je potrebné, aby jedna z jeho hmôt zostala konštantná; V tomto prípade T: 2 gramy.

Preto v týchto troch zlúčeninách určíme podiely hmotnosti C:

  • Tón2C: 1 gram c/2 gramy t
  • TC: 2 gramy c/2 gramy t
  • Tón2C3: 3 gramy c/2 gramy t

Budeme mať vzťah k hmotnosti C rovnajúcej sa 1: 2: 3. To znamená, že v TC je 2 -krát viac C ako v T2C a trikrát viac c v t2C3 ako v t2C. Ako je vidieť, 1: 2: 3 sú malé celé čísla (nepresahujú ani tucet).

Príklady zákona viacerých rozmerov

V nasledujúcich príkladoch sa uplatňujú rovnaké predchádzajúce kroky, ale vezmeme do úvahy molárne masy príslušných prvkov, za predpokladu, že jeden mól zlúčeniny.

Kokos2

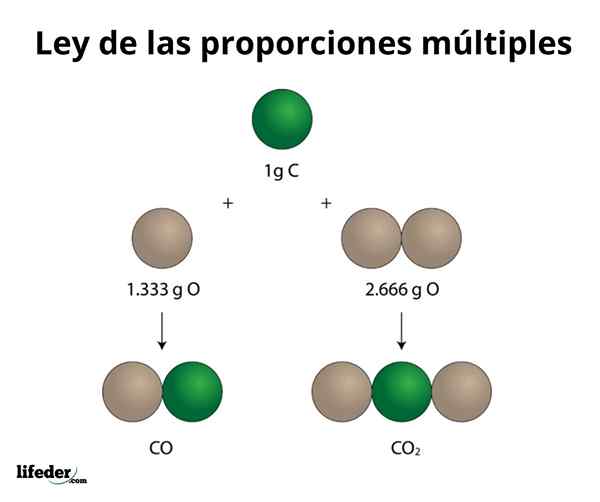
Tento príklad jednoduchým spôsobom vysvetľuje, ako funguje zákon viacerých rozmerov; V CO (oxid uhoľnatý) je tu 1.333 gramov kyslíka pre každý gram uhlíka. V oxidu uhličitého (CO₂) sú 2.666 gramov kyslíka pre každý gram uhlíka. Preto podiel kyslíka v oboch zlúčeninách je 1: 2, malé celé číslo.

H2O-h2Ani2

Zákon o viacerých rozmeroch sa vzťahuje na pár H2O-h2Ani2.

Môže vám slúžiť: 30 príkladov chemických suspenzií

V mol h2Alebo, 2 gramy vodíka sa kombinujú so 16 gramami kyslíka. Medzitým v mol h2Ani2, 2 gramy vodíka sa kombinujú s 32 gramami kyslíka. Aby sme overili, či je tento zákon splnený, musíme nastaviť rovnakú hmotnosť pre jeden z prvkov v oboch zlúčeninách. Tento čas je vodík: 2 gramy.

Hromadné proporcie pre h2Alebo h2Ani2 sú:

  • H2O: 16 gramov alebo/2 gramy h
  • H2Ani2: 32 gramov alebo/2 gramy h

Pomer hmotnosti O bude 16:32. Môžeme to však zjednodušiť rozdelením o 16, zostať 1: 2. Konečný vzťah sa opäť skladá z malých celých čísel.

SW2-SW3

V mol2, 32 gramov síry sa kombinuje s 32 gramami kyslíka. Medzitým v móle SO3, 32 gramov síry sa kombinuje so 48 gramami kyslíka. Hmotnosť síry je rovnaká pre obe zlúčeniny, takže môžeme priamo porovnávať proporcie kyslíka:

  • SW2: 32 gramov alebo
  • SW3: 48 gramov alebo

Byť pomerom kyslíkovej hmoty medzi oboma zlúčeninami rovnajúcimi sa 32:48 alebo 1: 1.5. Ale nebolo tam, že by mali byť celé čísla? Vzťah 1: 1.5 (1/1.5) Dá sa tiež napísať ako 2: 3 (0.6) a opäť budeme mať malé celé čísla: 2 a 3.

Všimnite si, že by sme mohli tiež napísať vzťah ako 48:32 alebo 1.5: 1, čo je výsledkom 3: 2. Zákon sa nemení, iba interpretácia vzťahu: existuje 1.5 alebo 3/2 krát viac kyslíka v SO3 že v SO2; čo je to isté, čo hovorí, že existujú 2/3 alebo 0.6 -krát menej kyslíka v SO2 že v SO3.

NIE NIE2-N2O-n2Ani3-N2Ani5

Zákon je možné uplatniť aj pre sériu zlúčenín. Zvážte oxidy dusíka: nie nie2-N2O-n2Ani3-N2Ani5. Aby sme v nich vyhodnotili tento zákon. Pretože? Pretože nie a nie2 Majú atóm dusíka menej ako ostatné oxidy:

  • 2 (č.): 28 gramov n/32 gramov alebo
  • 2 (nie2): 28 gramov n/64 gramov alebo
  • N2O: 28 gramov n/ 16 gramov alebo
  • N2Ani3: 28 gramov n/ 48 gramov alebo
  • N2Ani5: 28 gramov n/ 80 gramov alebo
Môže vám slúžiť: kyselina hypofyzárna (H3PO2): Vlastnosti, použitie a činidlá

Zabudnime na dusík a zamerajte sa na gramy kyslíka:

  • 2 (č.): 32 gramov alebo
  • 2 (nie2): 64 gramov alebo
  • N2O: 16 gramov alebo
  • N2Ani3: 48 gramov alebo
  • N2Ani5: 80 gramov alebo

Byť pomerom hmotností alebo rovnajúcich sa 32: 64: 16: 48: 80. Aby sme to zjednodušili, rozdeľujeme všetky svoje čísla medzi najmenšie, 16, ktoré sú ako 2: 4: 1: 3: 5.

To znamená, že v NO sú: 2 -krát viac kyslíka ako v n2Alebo, 4 -krát viac kyslíka v no2 že v n2Alebo, trikrát viac kyslíka v n2Ani3 že v n2Alebo a 5 -krát viac kyslíka v n2Ani5 že v n2Ani. Opäť máme malé celé čísla v rozmedzí od 1 do 5.

Obmedzenia

Zákon viacerých rozmerov nie je vždy splnený. Napríklad molárne masy alebo atómové hmotnosti prvkov nie sú celé čísla, ale majú veľa desatinných miest. To úplne upravuje vypočítané vzťahy, ktoré prestanú byť jednoduché.

Podobne nie je zákon splnený pre ťažké zlúčeniny, napríklad niektoré uhľovodíky. Napríklad unekano, cjedenásťH24, má 1.0083 alebo 121/120 krát viac vodíka ako dekan, c10H22, ktorého vzťah sa skladá z 121 a 120, ktoré presahujú tucet; Nie sú to malé celé čísla.

A nakoniec, zákon zlyhá s ne -stoichiometrickými zlúčeninami, rovnako ako pri mnohých oxidoch a sulfidoch.

Záver

Zákon o viacerých proporciách uvádza, že keď dva prvky tvoria viac ako jednu zlúčeninu, rôzne hmotnosti prvku, ktorý sa kombinuje s rovnakou hmotnosťou druhého prvku, sú v podiele malého počtu.

Odkazy

  1. Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Učenie sa.
  2. Wikipedia. (2020). Zákon viacerých rozmerov. Zdroj: In.Wikipedia.orgán
  3. Redaktori Enyclopaedia Britannica. (2020). Zákon viacerých rozmerov. Získané z: Britannica.com
  4. Chémia. (4. júna 2019). Zákon viacerých rozmerov od Daltona. Získané z: ChemistryGod.com
  5. Garcia nissa. (2020). Zákon viacerých rozmerov: Definícia a príklad. Štúdium. Získané z: štúdie.com