Faraday Formula Law, jednotky, experimenty, cvičenie,

Ten Faradayov zákon V elektromagnetizme sa uvádza, že meniaci sa prietok magnetického poľa je schopný vyvolať elektrický prúd v uzavretom obvode.

V roku 1831 anglický fyzik Michael Faraday zažil pohybujúce sa vodičov vo vnútri magnetického poľa a tiež rôzne magnetické polia, ktoré prekročili pevné ovládače.

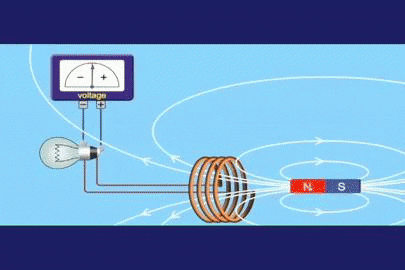postava 1. Indukčný experiment Faraday

Faraday si uvedomil, že ak mení prietok magnetického poľa v čase, bol schopný vytvoriť napätie úmerné uvedenej variácii. Ak je ε indukované elektromotorické napätie alebo sila (indukovaná FEM) a φ je tok magnetického poľa, v matematickej forme, môže sa vyjadriť:

| ε | = Δφ/Δt

Kde symbol δ označuje variácie množstva a tyče v fem označujú absolútnu hodnotu tohto. Pretože ide o uzavretý obvod, prúd môže cirkulovať v jednom alebo druhom smere.

Magnetický tok, ktorý je vyrobený magnetickým poľom cez povrch, sa môže napríklad meniť rôznymi spôsobmi:

-Pohybovanie magnetu typu cez kruhovú špirálu.

-Zvyšovanie alebo znižovanie intenzity magnetického poľa, ktoré prechádza cez slučku.

-Opúšťanie poľa pevne, ale určitým mechanizmom mení oblasť slučky.

-Kombinácia vyššie uvedených metód.

Obrázok 2. Anglický fyzik Michael Faraday (1791-1867).

[TOC]

Vzorce a jednotky

Predpokladajme, že existuje uzavretý obvod oblasti A, ako je kruhová špirála alebo povstanie rovnajúce sa s obrázkom 1, a že existuje magnet, ktorý vytvára magnetické pole B.

Tok magnetického poľa φ je skalárne množstvo, ktoré sa týka množstva poľných čiar, ktoré prechádzajú oblasťou a. Na obrázku 1 sú biele čiary, ktoré zanechávajú severný pól magnetu a vracajú sa na juhu.

Môže vám slúžiť: Brayton cyklus: proces, efektívnosť, aplikácie, cvičenia

Intenzita poľa bude úmerná počtu riadkov na jednotku plochy, takže vidíme, že na póloch je veľmi intenzívny. Môžeme však mať veľmi intenzívne pole, ktoré nevytvára prietok v slučke, ktoré môžeme dosiahnuť zmenou orientácie tohto (alebo magnetu).

Aby sa zohľadnil faktor orientácie, je tok magnetického poľa definovaný ako skalárny produkt medzi B a n, bytosť n Normálny jednotkový vektor na povrch spázy, ktorý naznačuje jeho orientáciu:

Φ = B•n A = ba.cosθ

Kde 9 je uhol medzi B a n. Ak napríklad B a n Sú kolmé, tok magnetického poľa je neplatný, pretože v takom prípade je pole dotýka.

Namiesto toho B a n Sú rovnobežné, to znamená, že pole je kolmo na rovinu Spira a čiary cez ňu prechádzajú maximum.

Medzinárodná systémová jednotka pre F je Weber (W), kde 1 w = 1 t.m² (číta „Tesla na meter štvorcový“).

Lenzov zákon 

Na obrázku 1 vidíme, že polarita napätia sa mení, keď sa magnet pohybuje. Polarita je stanovená Lenzovým zákonom, v ktorom sa uvádza, že indukované napätie sa musí postaviť proti variácii, ktorá ju produkuje.

Ak sa napríklad zvýši magnetický tok produkovaný magnetom, vodič stanoví prúd, ktorý cirkuluje vytváranie vlastného toku, čo je proti tomuto zvýšeniu.

Ak naopak, prietok vytvorený magnetom klesá, indukovaný prúd cirkuluje takým spôsobom, že jeho vlastný tok pôsobí proti poklesu.

Môže vám slúžiť: teplometrické stupnice

Aby sa tento fenomén zohľadnil, je negatívny znak Faradayovho zákona predložený a už nie je potrebné umiestniť pruhy absolútnej hodnoty:

ε = -5/Δt

Toto je zákon Faraday-Lenz. Ak je variácia prietoku nekonečná, delty sa nahradia diferenciálmi:

ε = -dφ/dt

Predchádzajúca rovnica je platná pre slučku. Ale ak máme rotovú cievku, výsledok je oveľa lepší, pretože FEM sa znásobuje n krát:

ε = - n (dφ/dt)

Experimenty Faraday

Na výrobu prúdu, ktorý rozsvieti žiarovku, medzi magnetom a špirálou musí existovať relatívny pohyb. Toto je jeden zo spôsobov, ako sa môže tok meniť, pretože takto intenzita poľa, ktorý prechádza menou slučky.

V okamihu pohybu magnetu prestane, žiarovka zhasne, aj keď je magnet ponechaný stále v spáze. Čo je potrebné na cirkuláciu prúdu do žiarovky, je to, že tok poľa sa mení.

Keď sa magnetické pole v priebehu času líši, môžeme ho vyjadriť ako:

B = B (T).

Udržiavaním konštantnej plochy a konštantnej ploche a nechápaním ho pripevneného v konštantnom uhle, ktorý je v prípade obrázku 0 °, potom:

 Pre slučku na obrázku 1 (cos 0 ° = 1):

Slapka

Ak dokážete zmeniť oblasť Scase, ponecháte jej orientáciu a upevnenie do stredu konštantného poľa, indukovaný FEM je daný:

Jedným zo spôsobov, ako to dosiahnuť, je dať lištu, ktorá sa posúva na vodivú koľajnicu určitou rýchlosťou, ako je znázornené na nasledujúcom obrázku.

Môže vám slúžiť: ío (satelit) Obrázok 3. Posuvník. Zdroj: Serway, r. Fyzika pre vedu a inžinierstvo.

Bar a koľajnica, plus žiarovka alebo odpor spojená s vodičom, tvoria uzavretý obvod vo forme obdĺžnikového spary.

Pri posuve tyče, dĺžka X Zvyšuje sa alebo klesá as ním oblasť zmien slučky, ktorá je dostatočná na vytvorenie premenlivého toku.

Variácia magnetického toku rotáciou

Ako sme už povedali, ak je uhol medzi B A normálny slučkový postup je rôzny, tok poľa sa mení podľa:

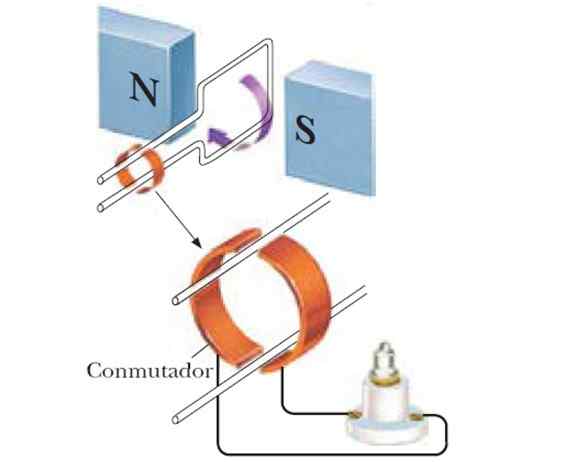Obrázok 4. Ak sa slučka otáča medzi pólmi magnetu, získa sa sínusový generátor. Zdroj: f. Zapata.

Tak sa získa sínusový generátor a ak sa použije jediný počet cievok, indukovaný FEM je väčší:

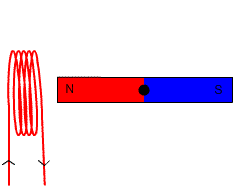Obrázok 5. V tomto generátore sa magnet otáča, aby sa vyvolal prúd v cievke. Zdroj: Wikimedia Commons.

Cvičenie

Kruhová cievka n kôl a rádio. Nájdite expresiu pre maximálnu indukovanú FEM v cievke.

Riešenie

Expresia pre FEM indukovanú rotáciou sa aplikuje, keď cievka má N Kláty, s vedomím, že:

-Plocha cievky je a = πr²

-Uhol 9 sa líši v závislosti od času ako 9 = Ωt

Je dôležité vziať do úvahy, že 9 = Ωt sa prvýkrát vymení v Faradayovom zákone a potom Je odvodený z času:

ε = -nba (cos θ) '= -nb (πr²).[cos (ωt)] '= nbΩ (πr²) Sen (Ωt)

Pretože sa požaduje maximálna FEM, vyskytuje sa to vždy, keď Sen ωt = 1, takže nakoniec:

ε_maximálny = NbΩ (πr²)

Odkazy

1. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 6. Elektromagnetizmus. Editoval Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fyzika. Druhé vydanie. McGraw Hill.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Edimatizovať. Sála.
4. Resnick, r. 1999. Fyzický. Zvuk. 2. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 2.