Ampère Formula a Rovnice zákon, demonštrácia, cvičenia

Ten Zákon uvádza, že obeh magnetického indukčného vektora B Je úmerný intenzite a prúdu, ktorý tečie rovnakým.

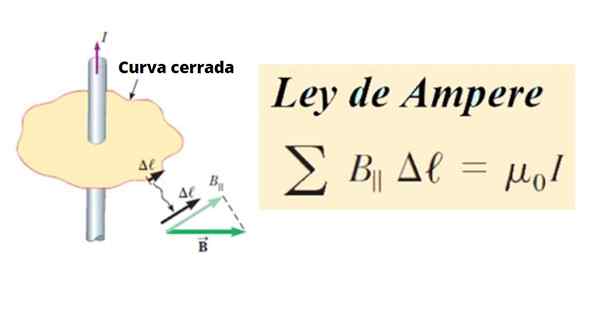
Zase obeh B Je to súčet všetkých výrobkov medzi tangenciálnym komponentom B_║ a dĺžka malého segmentu ℓ uzavretej krivky C, Okolo okruhu. Z matematického hľadiska je napísané takto:

∑ b_║ .ℓ ∝ Jo

postava 1. Definícia ampérického zákona. Zdroj: Serway, r. Fyzika vysokej školy.

Ako ľubovoľná čiara alebo krivka ju možno rozdeliť na malé segmenty ℓ, A tieto môžu byť na druhej strane nekonečné, potom sa nazývajú dℓ.

V tomto prípade sa suma stáva neoddeliteľnou líniou skalárneho produktu medzi vektormi B a dsiež. Tento produkt obsahuje tangenciálnu zložku B, ktorá je b cosθ, kde 9 je uhol medzi vektormi:

Malý kruh, ktorý prekračuje integrál, znamená, že integrácia sa vykonáva na uzavretej trajektórii C, ktorá v tomto prípade zahŕňa prúd prúdiaci cez prierez vodiča.

Konštanta proporcionality potrebná na stanovenie rovnosti je μ_ani, Vákuová priepustnosť. Týmto spôsobom zostáva Ampèreov zákon:

Zákon Ampère nám hovorí, že línia integrál ∫_C B ∙ Dsiež Stojí za to presne μ_aniJa, ale neponúka nám podrobnosti o tom, ako je magnetické pole orientované B Pokiaľ ide o krivku C v každom bode alebo o tom, ako vypočítať integrál. Hovorí nám iba, že výsledkom je vždy μ_aniJo.

[TOC]

Demonštrácia zákona Ampère

Ampèrov zákon sa overuje experimentálne kontrola magnetického poľa produkovaného veľmi dlhým priamym vodičom. Pred riešením problému sa musia zdôrazniť dva prípady osobitného záujmu v predchádzajúcej rovnici:

Môže vám slúžiť: svetelné telá: Charakteristiky a spôsob, akým generujú svoje vlastné svetlo

-Prvým je kedy B a dsiež Sú paralelné, čo znamená B je tangenciálne k C. Potom je uhol medzi oboma vektormi 0 ° a skalárny produkt je jednoducho produktom veľkosti B.ds.

-Druhý dochádza, ak B a dsiež Sú kolmé, v takom prípade je skalárny produkt 0, pretože uhol medzi vektormi je 90 °, ktorého kosínus je 0.

Ďalším dôležitým detailom je výber krivky C, na ktorej sa hodnotí obeh poľa. Zákon Ampère nešpecifikuje, čo môže byť, ale musí zabaliť súčasné rozdelenie. Ani nehovorí, ako cestovať po krivke a na to existujú dve možnosti.

Riešením je priradiť znaky podľa pravidla pravého palca. Štyri prsty sú zakrivené v smere, v ktorom sa chcete integrovať, zvyčajne to bude v teréne rovnaké B cirkulovať. Ak aktuálne ukazuje smer v pravom palec, je priradené znamenie a ak nie, podpíšte -.

To platí, keď existuje distribúcia s niekoľkými prúdmi, niektoré môžu byť pozitívne a iné negatívne. Algebraická suma z nich je to, čo sa chystáme umiestniť do zákona Ampère, ktorý sa zvyčajne vymenuje za Neochvejný prúd (Pre krivku c).

Magnetické pole priamočiara a nekonečného drôtu

Obrázok 2 zobrazuje drôt, ktorý prepravuje prúd a z roviny. Pravidlo pravého palca to zaisťuje B Cirkuluje opačným smerom a opisuje obvody, ako ukazujú červené šípky.

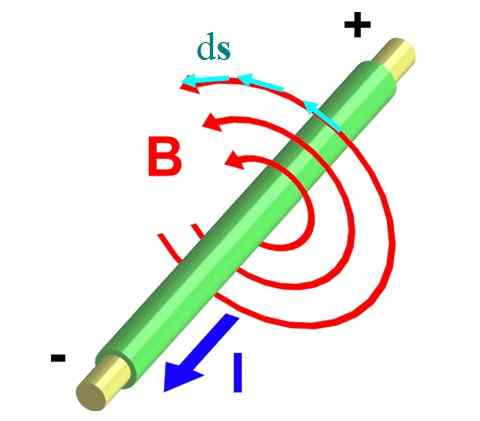Obrázok 2.- Magnetické pole nekonečného drôtu. Zdroj: Wikimedia Commons.

Vezmime si jedného z nich, ktorého polomer je r. Rozdelíme ho na malé diferenciálne segmenty dsiež, zastúpené pomocou modrých vektorov. Oba vektory, B a dsiež, Sú paralelné v každom bode obvodu, a tak integrálnymi ∫_C B ∙ Dsiež Transformuje sa v:

Môže vám slúžiť: Priamy prúd

∫_C BDS

Je to preto, že, ako sme už povedali, skalárny produkt B ∙ Dsiež  Je to produkt veľkosti vektorov 0 ° kosínus. Výsledok integrálu je známy vďaka zákonu Ampère, preto píšeme:

∫_C BDS = μ_aniJo

Pretože veľkosť poľa je konštantná v celej trajektórii, ponecháva integrál:

B ∫_C DS = μ_aniJo

Integrál ∫_C DS predstavuje súčet všetkých nekonečných segmentov, ktoré tvoria obvod rádií r, Rovnocenné s jeho dĺžkou, produkt jeho polomeru o 2π:

B.2πr = μ_aniJo

A odtiaľ zistíme, že veľkosť B je:

B = μ_aniI / 2πr

Je potrebné zdôrazniť, že aj keď je vybratá trajektória (alebo amperský obvod) Nie kruhový, výsledkom integrálu je stále μ_aniI, avšak ∫_C B ∙ Dsiež Už by to nebolo b.2πr.

Preto užitočnosť zákona Ampère na určenie magnetického poľa spočíva v výbere distribúcií s vysokou symetriou, takže integrál sa dá ľahko vyhodnotiť. Túto požiadavku spĺňajú kruhové a rektilineárne trajektórie.

Vyriešené cvičenia

- Cvičenie 1

Zvážte krivky A, B, C a D znázornené na obrázku 3. Zabalia tri prúdy, dva, ktoré opúšťajú lietadlo, symbolizované jedným bodom ( . ), ktorých intenzity sú 1 A a 5 A a prúd, ktorý vstupuje do lietadla, ktorý je označený krížom a ktorého veľkosť je 2 a.

Nájdite prúd uzavretý každou krivkou.

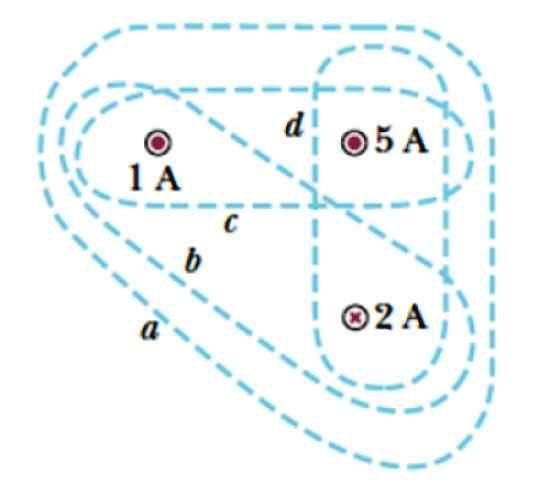Obrázok 3. Niekoľko kriviek na uplatnenie zákona Ampère. Zdroj: Serway, r. Fyzika vysokej školy.

Riešenie

Prúdy, ktoré opúšťajú papier, sú pridelené znamenie +. Na základe tohto:

Môže vám slúžiť: Povrchové vlny: Charakteristiky, typy a príklady

Krivka a

Uzatvára tri prúdy, preto je uzavretý prúd + 1 a + 5 a - 2 a = 4 a.

Krivka B

Vo vnútri tejto krivky sú iba prúdy 1 a y - 2 a, preto uzavretý prúd je od - 2 a.

Krivka c

Obsahuje odchádzajúce prúdy 1 a 5 A, preto je uzavretý prúd 6 a.

Krivka D

Prúdy vo vnútri sú +5a a - 2 a, potom uzatvárajú čistý prúd 3.

- Cvičenie 2

Vypočítajte veľkosť magnetického poľa produkovaného veľmi dlhým priamym drôtom.

Riešenie

Podľa zákona Ampère je pole drôtu dané:

B = μ_aniI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 Tón.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 6. Elektromagnetizmus. Editoval Douglas Figueroa (USB).
2. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup.  Pearson.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 2.
4. Serway, r. 2009. Fyzika vysokej školy. Učenie sa.
5. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 2. Redaktor sa vrátil.