Homologické strany

Vysvetlíme, aké sú homológne strany, s vyriešenými príkladmi a cvičeniami

Čo sú homológne strany?

Ten homologické strany V dvoch plochých geometrických číslach sú tie, ktoré si navzájom zodpovedajú, udržiavajúc podobnosť. Napríklad pravá ruka človeka je homológna s pravou rukou inej osoby.

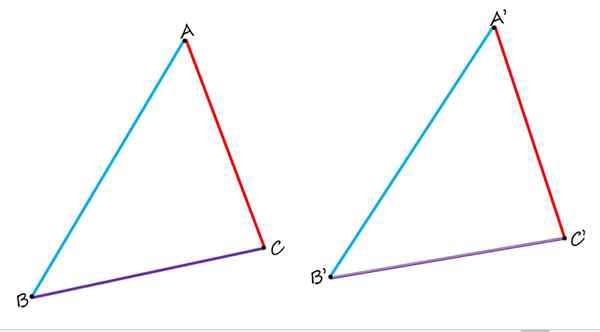
V plochej geometrii existujú nielen homológne strany, ale aj vrcholy a homológne uhly. Ak to chcete vidieť, zvážte nasledujúcu hodnotu, ktorá pozostáva z dvoch rovnakých trojuholníkov ABC a A'B'C ':

V zobrazených dvoch rovnakých trojuholníkoch sú AB a A'B 'homológne, ako aj strany BC a B'C' a AC a A'C '. Zdroj: f. Zapata.

Pri ich porovnaní je jasne pozorované, že strany ab a a'b 'v modrej farbe sú homológne, pretože v každom trojuholníku zaberajú podobnú polohu. Strany bc a b'c 'vo fialovej farbe sú tiež homológne. A nakoniec, červená strana AC je homologická s bočnou a'c '.

Vysvetlenie

Z vyššie uvedeného z toho vyplýva, že homológne strany sú tie, ktoré zaberajú rovnakú relatívnu polohu na obrázkoch rovnakým spôsobom. Na predchádzajúcom obrázku sa na zobrazenie myšlienky použili dva rovnaké trojuholníky, ale to môže ľahko zovšeobecniť ďalšie ploché geometrické čísla, ktoré tvoria po sebe nasledujúce strany, ktoré sa zatvárajú.

Tieto čísla sa volajú polygóny. Napríklad trojuholníky a kvadrilaterály sú polygóny 3 a 4 strany.

Koncept homológnych strán je dôležitý, pretože umožňuje definovať kritériá podobnosti medzi polygónmi, ako bude vidieť čoskoro. Podobné čísla majú presne rovnaký tvar a udržiavajú rovnaký pomer medzi ich stranami, aj keď nie sú rovnaké.

A hoci sa doteraz odkazoval iba na ploché čísla, sú tiež podobné čísla v troch rozmeroch. Ľahko sa pozorujú v policiach supermarketov, keď sa ten istý produkt predáva v rovnakých nádobách, ale s inou veľkosťou.

Môže vám slúžiť: matematická logika

Iné slová, ktoré sa používajú zameniteľne v geometrii, na označenie homológnych strán v geometrických číslach sú: zodpovedajúce strany, príslušné strany a ekvivalentné strany.

Homologické vrcholy a uhly

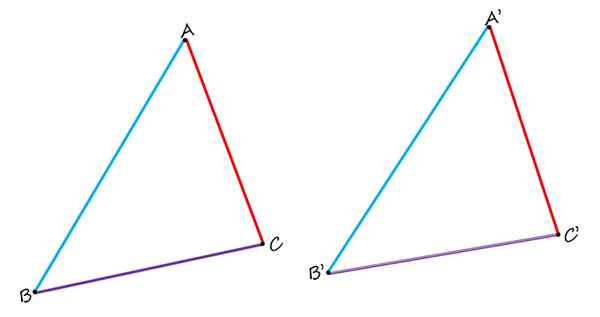
Rovnako ako v prípade strán sú definované aj homológne vrcholy, ktoré spájajú páry homológnych strán. Napríklad vrcholy A a 'z predchádzajúceho čísla sú homológne. Podobne sú páry vrcholov b a b 'a c a c' homológne.

Nakoniec homológne uhly zaberajú rovnakú relatívnu polohu v obrázkoch. Vrcholy homológnych uhlov sú zase homológne.

Na ilustráciu tejto myšlienky urobte uhol medzi modrou a fialovou stranou ľavého trojuholníka, ktorý je možné označiť ako ∠ABC. Tento uhol má svoj náprotivok pod uhlom ∠A'B'C ', od trojuholníka doprava.

Vrchol tohto uhla je B, ktorý, ako už bolo uvedené, je náprotivkom s B 'a ďalšie dva páry homológnych uhlov zobrazených trojuholníkov sú:

• ∠BCA a ∠B'C'a '
• ∠CAB a ∠C'A'B '

Podobnosť polygónov

Aby boli akékoľvek dva polygóny podobné, musia sa splniť tieto podmienky:

• Všetky páry homológnych uhlov majú rovnaké opatrenie
• Jeho páry homológnych strán sú úmerné.

Tieto dve podmienky musia byť splnené súčasne, aby sa zabezpečila podobnosť. Okamžite sa pozoruje prečo.

Na nasledujúcom čísle existujú dva kvadrilaterály, ktoré zjavne nie sú podobné. Je to kvôli skutočnosti, že sa splní prvý štatút týždenníka, ale druhý nie:

Dva kvadrilaterály, ktoré nie sú podobné, hoci ich homológne uhly majú rovnakú mieru. Zdroj: f. Zapata.

Zatiaľ čo v číslach majú ich páry homológnych uhlov rovnaké opatrenie, pretože všetky sú priame uhly (merajú 90 °), čísla nie sú podobné, pretože ich páry bokov nie sú proporcionálne.

Môže vám slúžiť: Injektívna funkcia: z čoho pozostáva, na čo ide a príklady

Na druhej strane, tieto dva kvadrilaterály majú homológne strany s rovnakou mierou, ale homológne uhly nemeria to isté. Preto údaje zjavne nie sú podobné.

Dva kvadrilaterály s homológnymi stranami toho istého opatrenia, ale s rôznymi vnútornými uhlami, preto nie sú podobnými číslami. Zdroj: f. Zapata.

Dôvod

Ak sú dve čísla podobné, kvocient medzi homológnymi stranami je rovnaký a nazýva sa to dôvod.

Označovanie strán jednej z obrázkov, ako sú a, b, c, d ... a zodpovedajúce z druhej postavy ako a ', b', c ', d

Obvody a oblasti podobných čísel

Pomer podobnosti umožňuje získavať vzťahy medzi obvodmi, oblastiami a objemami dvoch podobných obrázkov.

Obvodový dôvod pre dve podobné čísla

Obvod P polygón je definovaný ako súčet všetkých jeho strán. Ak máte postavu, ktorej strany sú „, b ', c', d '..., jeho obvod P' je:

P '= a' + b ' + c' + d '.. .

Ak je tento polygón podobný tomu a jeho strany sú a, b, c, d ..., splní sa to:

A preto:

A = r ∙ a '

To isté môžete potvrdiť pre ostatné strany tohto obrázku. Takže obvod P je vyjadrený ako:

P = a + b + c + d .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Pretože "R" je spoločným faktorom pre všetkých závislých, vzťah medzi P a P 'je:

P = r ∙ p '

To znamená, že dôvod obvodov medzi dvoma podobnými polygónmi sa rovná dôvodu podobnosti.

Dôvod oblastí dvoch podobných čísel

Ak majú dve podobné čísla, respektíve oblasti A a A ', sú spojené prostredníctvom:

Môže vám slúžiť: Cvičenia pre odbavenie vzorcov

A = r²∙ a '

Kde „R“ je dôvodom podobnosti čísel.

Objemový pomer dvoch podobných obrázkov

Sú to dve podobné tri rozmerové postavy, ktorých objemy sú V a V '. Vzťah medzi nimi prostredníctvom „R“ je:

V = r³∙ v '

Príklady

Plány

Časti pôdy, rastlina budovy alebo dokonca odev, v menšom rozsahu na liste papiera môžu byť zastúpené. Plány majú tú výhodu, že si môžete vziať so sebou a ľahko vykonať relevantné úpravy, predtým, ako uvádzajú do praxe skutočný objekt.

Mapy

Zvyčajne sú reprezentáciami v lietadle veľkej oblasti pôdy, od dediny po kontinenty. Sú tiež vyrobené v určitom rozsahu.

Majú početné aplikácie a existuje veľa typov. Napríklad prostredníctvom mapy je možné opísať terén a keď sa nachádza na konkrétnom bode, je určená najlepšia trasa, ktorá sa má dostať z tohto bodu do iného.

Modely

Sú to tri rozmerové reprezentácie v rozsahu objektov, ako sú autá, budovy a stavby všeobecne.

Cvičenie

Nasledujúce hodnoty zodpovedajú stranám niekoľkých podobných trojuholníkov. Nájdite dôvod podobnosti a hodnoty „X“ a „Y“:

Trojuholník 1: 5, 8, 10

Trojuholník 2: 150, x, y

Riešenie

Dôvodom podobnosti je kvocient:

R = 150/5 = 30

Preto:

x = 30 × 8 = 240

y = 10 × 30 = 300