Matematika

Lineárna interpolácia

4916
1544
Denis Škriniar

Vysvetľujeme, čo je lineárna interpoácia, jej vzorce, ako urobiť jeden, s vyriešenými príkladmi a cvičeniami

Čo je lineárna interpolácia?

Ten Lineárna interpolácia Skladá sa z odhadu umiestnenia bodu v číselnom intervale, za predpokladu, že extrémne hodnoty uvedeného intervalu sú spojené riadkom. Známe rovnicu tejto línie, je možné nájsť neznámy bod.

Myšlienka je schematizovaná na nasledujúcom obrázku, ktorý ukazuje prístup k grafu funkcie medzi bodmi A a B. Za predpokladu, že tieto body sú blízko, je možné priblížiť krivku, ktorá ich spája cez čiaru, a tým nájdete stredné body.

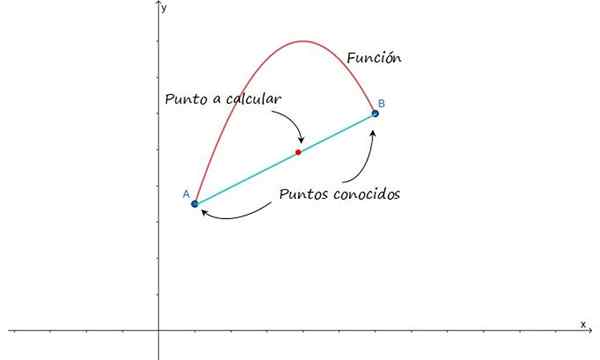postava 1.- Na vytvorenie lineárnej interpolácie medzi bodmi A a B je potrebné predpokladať, že sú zjednotení líniou . Zdroj: f. Zapata.

Môžete tiež priblížiť krivku, ktorá spája body uvedené pomocou kvadratickej funkcie alebo iného polynómu. Čiara má však výhodu z jej matematickej jednoduchosti, takže je ľahké ho zvládnuť, aj keď je najjednoduchšou interpoláciou všetkých, je možné, že výsledok nie je taký presný ako ten, ktorý získal pomocou iných funkcií.

Vzorce

Existujú dva súradnicové body [x_ani, f (x_ani)] a [x₁, f (x₁)], medzi ktorými patrí bod [x, g (x)], ktorého súradnice sú potrebné vedieť.

Prvý krok spočíva v tom, že sa pripojí k známym bodom cez segment čiary, na ktorom sa nachádzajú súradnice bodu.

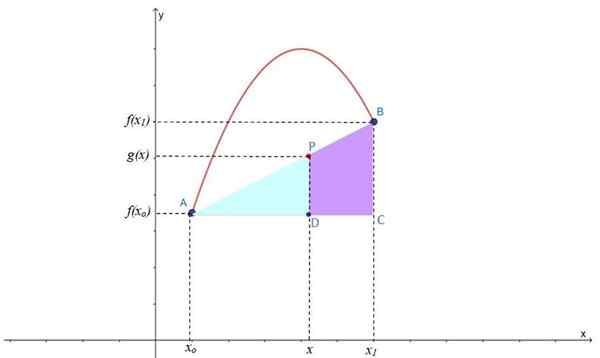Obrázok 2.- Lineárna interpolácia na nájdenie bodu P na interpovej čiare G (x), ktorá sa nachádza medzi bodmi A a B F (x). Zdroj: f. Zapata.

Ako vidíte, tvoria sa dva obdĺžniky: ABC a APD, ktoré majú spoločný akútny uhol, takže sú to podobné trojuholníky, na ktoré je možné aplikovať vetu Thales:

Môže vám slúžiť: analytická geometria

$\fracADAC=\fracAPAB=\fracPDBC$ Nahradenie miery segmentov podľa grafu sa získa nasledujúci vzťah:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Odtiaľ pokračujeme v vyčistení G (x):

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Volanie:

F₁(X₁) = y₁ ; F_ani(X_ani) = y_ani; g (x) = y

Horná rovnica sa transformuje na:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Rozsah chýb

Ak sa s touto metódou blíži funkcia, úroveň chýb je daná absolútnou hodnotou rozdielu medzi funkciou F (x) a interpolačnou čiarou G (x):

Chyba = │f (x) - g (x) │

Ako vytvoriť lineárnu interpoláciu?

Vykonanie lineárnej interpolácie je veľmi jednoduché, stačí sa riadiť týmito krokmi:

Krok 1

Stanovte neznámy bod P (x, y).

Krok 2

Stanovte dva body, ktoré obmedzujú interval, v ktorom sa nachádza hodnota, ktorá sa má nachádzať, to znamená body (x x_ani,a_ani) a (x₁, a₁).

Krok 3

Vymeňte všetky hodnoty v rovnici:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

A vypočítajte výsledok.

Príklady lineárnej interpolácie

Príklad 1

Chcete nájsť približnú hodnotu LN 3 prostredníctvom lineárnej interpolácie, vzhľadom na nasledujúce hodnoty:

ln 2 = 0.693147 a ln 4 = 1.386294

Porovnajte výsledok s hodnotou LN3 získanej prostredníctvom kalkulačky a určte spáchanú maržu.

Krok 1

Ak chcete nájsť približnú hodnotu LN 3, musíte postupovať nasledujúcim spôsobom: Po prvé, neznáme sa, čo je y = ln 3, vedľa jeho zodpovedajúcej hodnoty „x“: x = 3. Toto je bod, ktorý chcete vypočítať: (3, ln 3).

Krok 2

Potom musíte stanoviť limitné body intervalu so známymi hodnotami. Vyžaduje sa, aby to urobil s nasledujúcimi niekoľkými bodmi:

Dolná hranica: [x_ani = 2; a_ani = ln 2 = 0.693147]
Horná hranica: [x₁ = 4; a₁ = ln 4 = 1.386294]
Krok 3

Hodnoty stanovené v krokoch 1 a 2 sa starostlivo nahradia v rovnici, aby sa vytvoril výsledok prístupu k LN 3:

Môže vám slúžiť: Koľko riešení má kvadratickú rovnicu?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Skutočná hodnota LN3 získaná kalkulačkou je:

ln 3 = 1.098612

A marža chyby je:

Chyba = │1.098612 - 1.03971 │ = 0.059

Percentuálna chyba interpolácie sa vypočíta vydelením chyby medzi skutočnou hodnotou LN3 a vynásobením 100 %:

Percentuálna chyba = (skutočná chyba/hodnota) × 100 = (0.059/1.098612) × 100% = 5.4%

Príklad 2

Teraz chcete nájsť približnú hodnotu LN3 lineárnou interpoláciou, ktorá je známa tieto dve hodnoty:

ln 2.5 = 0.916291 a LN 3.5 = 1.252763

Určte tiež zodpovedajúcu chybu a porovnajte s výsledkami predchádzajúceho príkladu.

Krok 1

Opäť neznámy bod je:

y = ln 3, x = 3

Krok 2
Dolná hranica: [x_ani = 2.5; a_ani = y_ani = ln 2.5 = 0.916291]
Horná hranica: [x₁ = 3.5; a₁ = ln 3.5 = 1.252763]
Krok 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Preskúmanie hodnoty ponúkanej kalkulačkou:

ln 3 = 1.098612

Úroveň chýb je určená v tomto prípade, čo má za následok:

Chyba = │1.098612 - 1.084527 │ = 0.014

Percentuálna chyba v tomto prípade je ≈ 1.3 %. V porovnaní s úrovňou chýb v príklade 1 je nová hodnota presnejšia, pretože interval vybraný na interpolárny je nižší.

Vyriešené cvičenia

Cvičenie 1

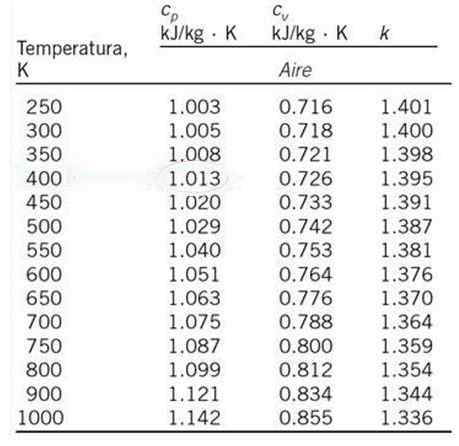
Vypočítajte lineárnou interpoláciou špecifické teplo vzduchu pri konštantnom tlaku C_p a teplota 530 K, počnúc od tabuľky hodnôt uvedených nižšie.

Riešenie

Pri riešení mnohých problémov je bežné, že požadovaná hodnota sa neobjavuje presne tak, ako je to požadované v tabuľke, ktoré sú dané hodnoty. Alternatívou je zvoliť hodnotu, ktorá je najbližšia k požadovanej, ale mnohokrát je dostatočná lineárna interpolácia na nájdenie oveľa lepšieho prístupu.

Môže vám slúžiť: Známky zoskupenia

Hodnota C_p V pripojenej tabuľke sa neobjaví 530 K, ale lineárna interpolácia sa môže uskutočniť s príslušnými špecifickými zahrievanami pri 500 K a 550 K, čo sú teploty najbližšie k 530 K a ktorých špecifické teploty sa objavujú v zobrazenej tabuľke.

Príslušné tepelné teploty pre tieto teploty sú:

Tón_ani = 500 K; c_po = 1.029 kj /kg ∙ k

Tón₁ = 550 K; c_P1 = 1.040 kj /kg ∙ k

A neznámy je bod (500 k, c_p)

Výmena vo vzorci lineárnej interpolácie uvedeného vyššie, s t na mieste premennej „x“ a c_p Namiesto „y“ máte:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Cvičenie 2

Zaťaženie aplikované na pružinu (v kilopondiách) produkuje tieto predĺženia (v milimetroch) podľa zobrazenej tabuľky:

Vypočítajte predĺženie, keď je zaťaženie 12.6 kp.

Riešenie

Nech a hodnota predĺženia požadovaného, keď je zaťaženie C = 12.6 kp. Neznámy bod je (12.6, y), čo patrí medzi body:

C_ani = 10 kp; a_ani = 105 mm

C₁ = 15 kp; a₁ = 172 mm

Zostáva iba nahradenie hodnôt v rovnici:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Navrhované cvičenie

Vypočítajte špecifické teplo tepla na konštantný objem pre teplotu 727 K pomocou lineárnej interpolácie a tabuľky cenných papierov cvičenia vyriešené 1.

Odkazy

Rafa Vilchez Academy. Ako vykonávať lineárnu interpoláciu. Zotavené z: Academiraafavilchez.com
Chapra, s. 2007. Numerické metódy pre inžinierov. 5. Vydanie. McGraw Hill.
Khanská akadémia. Matematika lineárnej interpolácie. Získané z: Khanacademy.orgán.
Vzdelávací život. Lineárna interpolácia. Získané z: TheeducationLife.com
X-inžinier. Lineárna interpolácia a extrapolácia s kalkulačkou. Obnovený z: x-engineer.orgán.

Lineárna interpolácia

Čo je lineárna interpolácia?

Vzorce

Rozsah chýb