Interpolácia LAGRANGE

Čo je interpolácia LaGrange?

Lagrangeova interpolácia je numerická metóda aproximácie funkcií, ktorá využíva polynóm, ktorý prechádza určitými známymi bodmi funkcie, ktorá je určená na priblíženie.

Ak je približná funkcia mäkká, dokonca aj mimo daných alebo známych hodnôt, polynóm berie hodnoty blízko hodnotám funkcie záujmu, najmä ak sú tieto hodnoty medzi danými bodmi. Preto sa polynóm považuje za dobrý prístup k tejto funkcii.

postava 1.- Vzorec na zostavenie lagrange polynómov. Zdroj: f. Zapata.

Teraz predpokladajme, že chcete priblížiť funkciu f (x) z ktorých v niektorých sú známe iba ich hodnoty X-_Jo-, s Jo od 0 až do N-1. To znamená, že sa navzájom poznajú n body (X-_Jo, a_Jo) s a_Jo = f (x_Jo), Kde index Jo Zmiznúť 0 až do N-1.

V metóde interpolácie Lagrange sa polynóm, ktorý sa blíži k funkcii f (x) Je to polynóm P (x) titul N-1, postavené lineárnou kombináciou n Polynómia L_Jo(X) titul N-1. Toto sú Polynómy lagrange, ktoré sú vyjadrené takto:

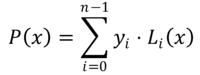
Hodnoty a_Jo Predstavujú súradnice zodpovedajúce Abscissovi X_Jo Kde funkcia f (x) Je to známe, to znamená: a_Jo = f (x_Jo).

Polynómy lagrange

Prostredníctvom lineárnych kombinácií medzi nimi pôsobia Lagrange Polynomials ako základ pre polynóm budovania stupňa N -1 ktoré budú slúžiť na interpolovanie n známe body.

Zápis polynómov je L_Jo(x), s indexom I v rozsahu od 0 do n-1. Vzorec na stanovenie polynómov Lagrange je nasledujúci:

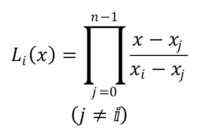
Zobrazený symbol naznačuje, že sa musí vykonať produkt N -1 monomialov, počnúc polynomiálnym j = 0.

Charakteristiky lagrange polynómov

1.- Lagrange polynómy sú presne rovnaké ako jednotka, keď sa hodnotia v Abscissu zodpovedajúcu ich indexu, to znamená:

L_Jo(X_Jo) = 1

2.- Sú zrušené v Abscissa interpolačných bodov s indexom odlišným od toho istého polynómu:

Môže vám slúžiť: Opisná štatistika: História, charakteristiky, príklady, koncepty

L_Jo(X_J) = 0, s i ≠ j.

3.- Lagrange Polynomials, ktorý vezme ďalšie hodnoty Abscissa odlišné od interpolačných bodov, získavajú hodnoty medzi -1 a +1.

4.- Na získanie polynómov lagrange je potrebné len poznať Abscissa bodov do interpoch.

Druhé polynómy Lagrange

Druhé polynómy LaGrange sú tie, ktoré sa používajú najčastejšie, keď chcete urobiť interpoláciu s tromi bodmi.

Predpokladajme, že interpolárna funkcia je známa v troch bodoch, ktoré sú:

(X₀,a₀); (X₁, a₁); (X₂, a₂)

Potom vaše zodpovedajúce lagrange polynómy L₀, L₁ a L₂ Dostanú sa takto:

L₀(x) = [(x - x₁) / (X₀ - X₁)] [(x - x₂) / (X₀ - X₂)]

L₁(x) = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)]

L₂(x) = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)]

Je potrebné poznamenať, že L₀(X₀) = L₁(X₁) = L₂(X₂) = 1, zatiaľ čo L_Jo(X_J) = 0 tak dlho Jo≠ j.

Interpolácia polynóm druhého stupňa

Je dôležité poznamenať, že v LaGrangeovom interpolácii polynómu sú súradnice interpolačných bodov Lagrange polynomiálne faktory.

Týmto spôsobom, akonáhle sa polynómy získajú pre určité hodnoty Abscissa, slúžia na výpočet interpolačného polynómu rôznych funkcií za predpokladu, že usporiadaný v predtým pevnej Abscissu je známy.

V prípade interpolácie druhého ročníka:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

A p (x) sa blíži funkcii f (x) v intervale (X₀, X₂).

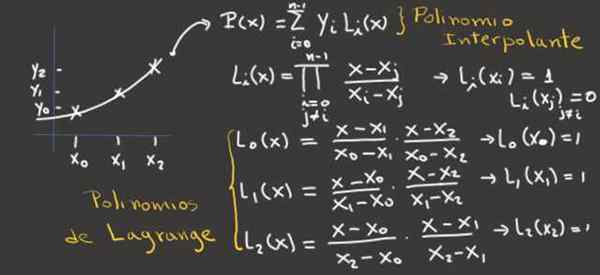Obrázok 2.- Tento obrázok ukazuje, ako získať Lagrange polynómy pre tri interpolačné body a od nich interpolingový polynóm. Zdroj: f. Zapata.

Príklady

Príklad 1

Nájdite Lagrange Polynomials zodpovedajúce trom bodom Abscissa X₀= 0, X₁= 1 a X₂= 2.

Ako je vidieť v predchádzajúcej časti, tieto polynómy budú:

Môže vám slúžiť: Prepríjemná funkcia: Definícia, vlastnosti, príklady

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( X² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - X)

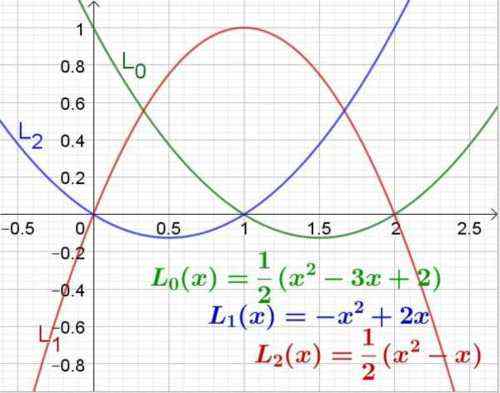Obrázok 3. Lagrange Polynomials pre hodnoty Abscissa 0, 1 a 2. Zdroj: f. Zapata.

Príklad 2

Chcete priblížiť funkciu f (x) = arcan (x) V intervale [0, 2]. Tejto funkcie sú známe iba ich hodnoty X₀= 0, X₁= 1 a X₂= 2, ktoré sú a₀= 0, a₁= π/4 = 0,785 a a₂= 1 107.

Preto musíte nájsť interpolingový polynóm P (x) blížiaci sa f (x) V uvedenom intervale.

V príklade 1 už boli stanovené polynómy Lagrange pre hodnoty Abscissa uvedené v tomto vyhlásení, takže nie je potrebné opakovať výpočet. Interpoling Polynomial bude teraz:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(X)

Čo je rovnocenné:

P (x) = y₀ L₀(x) + a₁ L₁(x) + a₂ L₂(X)

V tomto konkrétnom prípade je to:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - X)

Vyššie uvedené je zjednodušené na:

P (x) = 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - X)

A nakoniec zostáva:

P (x) = -0 2315 ∙ x² + 1 0165 ∙ x

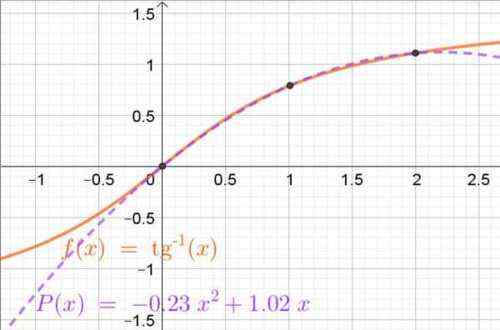Obrázok 4. Interpoling Polynomial získaný prostredníctvom lagrange polynómov, ktoré približujú funkciu oblúka-tangent v intervale (0, 2). Zobrazia sa aj interpolačné body. Zdroj: f. Zapata.

Cvičenia

Cvičenie 1

Získajte primerané polynómy Lagrange, aby ste mali prístup k tejto funkcii:

f (x) = sin (x)

V intervale [0, π] as piatimi interpolačnými bodmi.

Riešenie

V prvom rade sú stanovené Abscissa interpolačných bodov, ktoré sú vybrané rovnocenné a vrátane koncov aproximačného intervalu. S tým máte:

X₀= 0; X₁= π/4; X₂= π/2; X₃= 3 π/4; X₄= π.

Môže vám slúžiť: Nerovnosť trojuholníka: demonštrácia, príklady, vyriešené cvičenia

Pretože f (x) je zrušený v extrémnych bodoch, nebude potrebné získať polynómy Lagrange L L₀ a l₄.

Polynómia l₁, L₂ a l₃ sú:

L₁ = [(x - x₀) / (X₁ - X₀)] [(x - x₂) / (X₁ - X₂)] [(x - x₃) / (X₁ - X₃)] [(x - x₄) / (X₁ - X₄)]

L₂ = [(x - x₀) / (X₂ - X₀)] [(x - x₁) / (X₂ - X₁)] [(x - x₃) / (X₂ - X₃)] [(x - x₄) / (X₂ - X₄)]

L₃ = [(x - x₀) / (X₃ - X₀)] [(x - x₁) / (X₃ - X₁)] [(x - x₂) / (X₃ - X₂)] [(x - x₄) / (X₃ - X₄)]

Teraz nahradíme hodnotu Abscissa:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Menovatelia sú vyriešení:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Zjednodušilo sa a preskupilo sa, aby sa získalo:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Cvičenie 2

Získajte interpolačný polynóm, ktorý sa blíži k funkcii Sen (X) v intervale [0, π] s piatimi interpolačnými bodmi vybranými v cvičení 1 a ich príslušnými lagrangeovými polynómami.

Riešenie

Interpolačný polynóm je:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * L4

Vyhodnotenie funkcie sínusovej a znásobujúcej funkcie je:

P (x) = (√2/2) l₁ + 1 * l₂ + (--2/2) l₃

Po náročnej algebraickej práci je interpolačný polynóm:

P (x) = 2. 7481 x⁴ -pätnásť. 138 x³ +23. 467 x² - 9. 5236 x

Odkazy

1. Goodman, a. L. H. Devätnásť deväťdesiat šiestich. Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
2. Harpe, P. d. (2000). Témy v teórii geometrických skupín. University of Chicago Press.
3. Hazardinkel, m. (2001). Lineárna interpolácia “, Encyklopédia matematiky.
4. Hoffmann, e. (2002). K chronológii interpolácie: od starodávnej astronómie po moderné spracovanie signálu a obrazu. Konanie IEEE.
5. Wikipedia. Lagrange polynomiálna interpolácia. Získané z: Wikipedia.com