Vzájomná indukčná vzorca/koeficient, aplikácie, cvičenia

Ten vzájomná indukčnosť Opisuje interakciu medzi dvoma nadchádzajúcimi 1 a 2 cievkami, pomocou ktorých premenný prúd Jo Cirkulujú cez cievku 1, vytvára meniaci sa tok magnetického poľa, ktorý prechádza cievkou 2.

Tento tok je úmerný prúdu a konštanta proporcionality je vzájomná indukčnosť₁₂. Byť φ_B2 Tok magnetického poľa cez cievku 2, potom môžete napísať:

Φ_B2 = M₁₂ Jo₁

postava 1.- Transformátor je hlavnou aplikáciou vzájomnej indukčnosti. Zdroj: pixnio.

A ak má cievka 2 n₂ Kolá:

N₂ . Φ_B2 = M₁₂ Jo₁

Týmto spôsobom vzájomná indukčnosť alebo koeficient vzájomnej indukčnosti₁₂ Medzi oboma cievkami je:

M₁₂ = N₂ . Φ_B2 / Jo₁

Vzájomná indukčnosť má Weber/Amperio alebo WB/A jednotky, ktoré sa nazýva Henry alebo Henrio a skrátene H. Preto 1 Henry zodpovedá 1 WB/ a.

Hodnota m₁₂ Závisí to od geometrie medzi cievkami, ich tvarom, ich veľkosťou, počtom zákrut každého a vzdialenosti, ktorá ich oddeľuje, ako aj od relatívnej polohy medzi nimi.

[TOC]

Aplikácie vzájomnej indukčnosti

Fenomén vzájomnej indukčnosti má mnoho aplikácií vďaka skutočnosti, že jeho pôvod je v zákone Faraday-Lenz, ktorý uvádza, že premenlivé prúdy v obvode indukujú prúdy a napätie v inom, bez toho, aby boli obvody spojené s káblami pomocou káblov káble.

Keď dva obvody interagujú týmto spôsobom, hovorí sa, že sú magneticky spojené. Týmto spôsobom môže energia prejsť z jedného do druhého, okolnosť, ktorú možno použiť niekoľkými spôsobmi, ako to dokazuje Nikola Tesla na začiatku 20. storočia (pozri cvičenie vyriešené 1).

Vo svojom úsilí o prenos elektriny bez káblov, Tesla zažila s rôznymi zariadeniami. Vďaka svojim objavom bol vytvorený transformátor, zariadenie, ktoré sa pohybuje z elektriny z rastlín do domovov a priemyselných odvetví.

Môže vám slúžiť: jednotkové vektory: Charakteristiky, ako ho dostať von, príklady

Transformátor

Transformátor vysiela veľmi vysoké alternatívne napätie v elektrických vedeniach, čím minimalizuje tepelné straty a súčasne dodáva spotrebiteľom maximálnu energiu.

Keď sa napätie dosiahne, musí sa znížiť, čo sa dosiahne s transformátorom. Toto pozostáva z dvoch drôtových cievok, ktoré sa valili okolo železného jadra. Jedna z cievok s n₁ zákruty sú pripojené k alternatívnemu napätiu a nazýva sa primárne. Druhý, ktorý je sekundárny, má n₂ otočí sa, pripája sa k odporu.

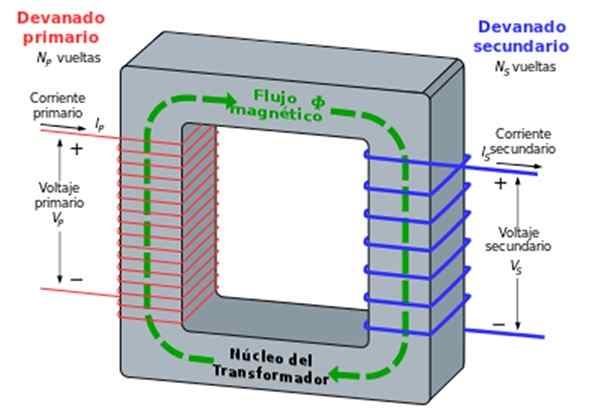Obrázok 2. Transformátor. Zdroj: Wikimedia Commons.

Železné jadro zaisťuje, že všetky riadky magnetického poľa, ktoré prechádzajú cievkou.

Faradayov zákon ustanovuje, že dôvod medzi napätím V₂ /V₁ (sekundárne /primárne) sa rovná dôvodu medzi počtom zákrut n₂ /N₁:

Vložka₂ /V₁ = N₂ /N₁

Správne nastavenie počtu zákrut, napätie väčšie alebo menej ako vchod sa získa pri výstupe.

Transformátory sú vyrobené z mnohých veľkostí, od obrovských transformátorov v elektrických inštaláciách až po nakladače mobilných telefónov, notebooky, MP3 a ďalšie elektronické zariadenia.

Kardiostimulátor

Účinky vzájomnej indukčnosti sú tiež prítomné v kardiostimulátore na udržanie frekvencie srdcového rytmu, takže môže udržať prietok krvi stabilný.

Kardiostimulátori pracujú s batériami. Keď sú vyčerpané, vonkajšia cievka je schopná prenášať energiu do inej cievky vo vnútri kardiostimulátora. Keďže postup sa vykonáva indukciou, nie je potrebné, aby pacienta predkladala nový zásah, keď je batéria vyčerpaná.

Môže vám slúžiť: Kalibračná krivka: Na čo je to, ako to urobiť, príklady

Bezdrôtové nakladače

Zatiaľ čo ďalšou bežnou aplikáciou sú bezdrôtové nakladače pre rôzne objekty, ako sú zubné kefy a mobilné telefóny, ktoré sú zariadeniami s nízkou spotrebou elektrickej energie.

V budúcnosti sa zvyšuje používanie bezdrôtových nakladačov pre elektrické automobilové batérie. A mnoho výskumov je dnes zamerané na výrobu bezdrôtovej elektriny v domácnostiach. Jedným z hlavných obmedzení momentov je vzdialenosť, v ktorej môžu byť prúdy indukované vďaka magnetickým poliam.

Vyriešené cvičenia

- Cvičenie 1

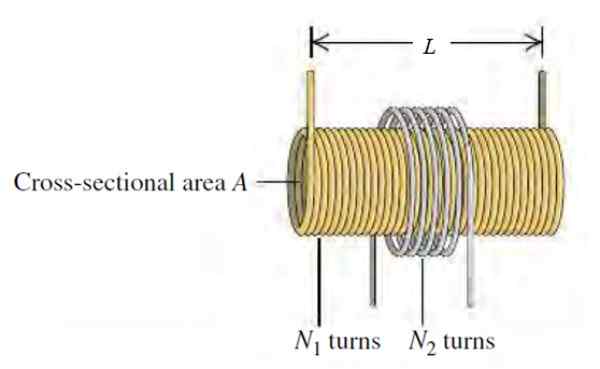
Vo verzii cievky Tesla, ktorá sa používa ako generátor s vysokým napätím v niektorých laboratórnych demonštráciách, je dlhá dĺžka L, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Radio R, Rádiu R₁ s n₁ kolo na dĺžku jednotky, koaxiálne obklopené kruhovým rádiobínom r₂ a n₂ kola.

Obrázok 3. Schéma cievky Tesla. Zdroj: Sears Zemansky. Fyzika univerzity.

a) Nájdite vzájomnú indukčnosť m obvodu, závisí od prúdu, ktorý cirkuluje solenoid?

b) Závisí vzájomná indukčnosť od tvaru cievky alebo od toho, či sú vaše zákruty viac -menej zvinuté dokopy?

Roztok

Veľkosť magnetického poľa solenoidu je úmerná počtu zákrut a prúd, ktorý sa cez neho cirkuluje, čo je označené ako ja₁, Pretože solenoid je obvod 1. Je daný výrazom:

B₁ = μ_aniN₁.Jo₁ / L

Tok magnetického poľa, ktorý solenoid vytvára v spire cievky, ktorá je obvod 2, je produktom intenzity poľa v oblasti spojenej s poľom:

Φ_B2 = B₁. Do₁

Kde₁ Je to oblasť prierezu solenoidu a nie cievku, pretože solenoidové pole je mimo neho neplatné:

Môže vám slúžiť: svetelné telá: Charakteristiky a spôsob, akým generujú svoje vlastné svetlo

Do₁ = π (r₁)²

Nahradíme oblasť v rovnici za φ_B2:

Φ_B2 = B₁. π (r₁)² = (μ_aniN₁.Jo₁ / L). π (r₁)²

A vzájomná indukčnosť je daná:

M₁₂ = N₂ . Φ_B2 / Jo₁ = N₂. [μ_aniN₁.Jo₁ / L). π (r₁)² ] / Jo₁

M₁₂ = μ_ani N₁ N₂ . π (r₁)² / L

Nezávisí od prúdu, ktorý cirkuluje solenoid, ktorý sme videli, že je zrušený.

Riešenie B

Ako vidíme, vzájomná indukčnosť nezávisí od tvaru cievky ani od sprísnenia ponožiek. Jediným vplyvom cievky v vzájomnej indukčnosti je počet zákrut prítomných, čo je n₂.

- Cvičenie 2

Dve cievky sú veľmi blízko seba a jedna z nich vykonáva premenlivý prúd v čase danej nasledujúcou rovnicou:

I (t) = 5.00 e ^{-0.0250 t} Sen (377 t) a

Pri t = 0.800 sekúnd sa meria indukované napätie v druhej cievke, získanie -3.20 V. Nájdite vzájomnú indukčnosť cievok.

Riešenie

Používame rovnicu:

ε₂ = - m₁₂ (dal₁/dt)

K vzájomnej indukčnosti medzi cievkami, ktoré jednoducho nazývame m, pretože zvyčajne m₁₂ = M_{dvadsaťjeden}. Budeme potrebovať prvý derivát prúdu vzhľadom na čas:

dal₁/dt =

= - 0.0250 x 5.00 e ^{-0.0250 t} x sin (377 t) - 377 cos (377 t) x 5.00 e ^{-0.0250 t}  Ace

Tento derivát hodnotíme v t = 0.800 s:

dal₁/dt = - 0.0250 x 5.00 e ^{-0.0250 x 0.800} X Sin (377 x 0.800) - 377 cos (377 x 0.800) x 5.00 e ^{-0.0250 x 0.800}  A/s =

= -5.00 e ^{-0.0250 x 0.800} [0.0250 x sen (377 x 0.800) + 377 cos (377 x 0.800)] =

= -1847.63 A/s

M = -3.20 V / -1847.63 A/S = 0.001732 h = 1.73 mh.

Odkazy

1. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 6. Elektromagnetizmus. Editoval Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.
3. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
4. Sears, f. (2009). University Physics Zv. 2.
5. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 2. 7. Edimatizovať. Učenie sa.