Demonštrácia pythagorských identifikácií, príklady, cvičenia

Byť Pythagorské identity Všetky trigonometrické rovnice, ktoré sú splnené pre akúkoľvek hodnotu uhla a sú založené na vete Pythagoras. Najslávnejšou z Pythagorovských identít je základná trigonometrická identita:

SEN²(a) + cos²(a) = 1

postava 1. Pythagorean trigonometrické identity.

Stále je dôležitý a používa pythagorskú identitu tangens a secant:

Tak²(a) + 1 = sec²(α)

A Pythagorovská trigonometrická identita, ktorá zahŕňa Cotangent a Harvester:

1 + ctg²(a) = CSC²(α)

[TOC]

Demonštrácia

Trigonometrické dôvody prsník a klimatizovať Sú zastúpené v obvode polomeru jeden (1) známy ako trigonometrický kruh. Tento kruh má centrum pri pôvode súradníc alebo.

Uhly sa merajú z pozitívnej semi -osi x, napríklad uhol a na obrázku 2 (pozri neskôr). Na rozdiel od hodinových rúk, ak je uhol pozitívny, a v smere rúk, ak ide o negatívny uhol.

Kreslenie je polo. Bod p je premietaný ortogonálne na horizontálnej osi X, ktorá vedie k bodu C. Podobne sa P premieta kolmo na vertikálnu os a vedie k bodu S.

Máte pravý trojuholník OCP v C. 

Prsia a kosínus

Je potrebné si uvedomiť, že trigonometrický dôvod prsník Je definovaný na pravom trojuholníku nasledovne:

Bosom uhla trojuholníka je pomer alebo pomer medzi katetom na rozdiel od uhla a hypotenusu trojuholníka.

Aplikované na trojuholník OCP na obrázku 2 by bolo takéto:

Sin (a) = cp / op

Ale CP = OS a OP = 1, takže:

Hriech (α) = OS

Čo znamená, že projekcia na osi y má hodnotu rovnajúcu sa znázornenému uhlu uhla. Je potrebné poznamenať, že maximálna hodnota prsníka uhla (+1) dochádza, keď α = 90 ° a minimálne (-1), keď a = -90 ° alebo a = 270 °.

Môže vám slúžiť: Vektorový priestor: základňa a rozmer, axiómy, vlastnosti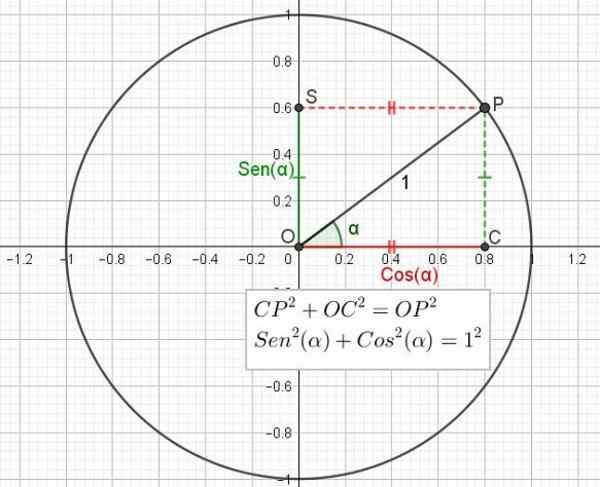Obrázok 2. Trigonometrický kruh ukazujúci vzťah medzi Pythagorasovou vetou a základnou trigonometrickou identitou. (Vlastné rozpracovanie)

Podobne aj kosínus uhla je pomer medzi kategóriou susediacou s uhlom a hypotenusom trojuholníka.

Aplikované na trojuholník OCP na obrázku 2 by bolo takéto:

Cos (a) = oc / op

Ale op = 1, takže:

Cos (a) = OC

Čo znamená, že projekcia OC na osi X má hodnotu rovnajúcu sa hodnote zobrazeného lona uhla. Je potrebné poznamenať, že maximálna hodnota kosínu (+1) sa vyskytuje, keď a = 0 ° alebo a = 360 °, zatiaľ čo minimálna hodnota kosínus je (-1), keď a = 180 °.

Základná identita

Pre obdĺžnik OCP trojuholníka sa aplikuje veta Pythagoras, ktorá uvádza, že súčet štvorca kategórií sa rovná štvorcovi hypotenusu:

Cp² + Oc² = Op²

Už sa však povedalo, že cp = os = sin (α), že OC = cos (α) a že OP = 1, takže predchádzajúci výraz možno prepísať v závislosti od sínusu a kosínus uhla:

SEN²(a) + cos²(a) = 1

Dotyčnica

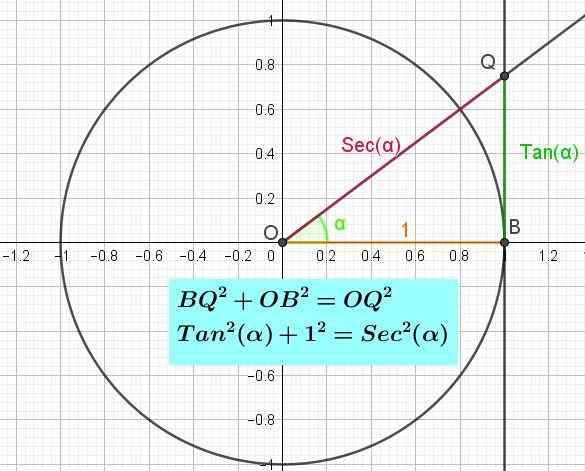
Rovnako ako os x v trigonometrickom kruhu je os kosínu a os a os prsníka, rovnakým spôsobom, ako je os dotyčnice (pozri obrázok 3), ktorá je presne líniou tangens k jednotke kruh v bode súradnice bodu B (1, 0). 

Ak chcete poznať hodnotu dotyčnice uhla, uhol sa čerpá z kladnej poloxle x, priesečník uhla s osou dotyčnice Definuje bod Q, dĺžka segmentu OQ je dotyčnica uhla.

Môže vám slúžiť: algebraické deriváty

Je to preto, že podľa definície je dotyčnica uhla a je opačným kateto QB medzi susedným katetom oboch. To znamená (α) = qb / ob = qb / 1 = qb.

Obrázok 3. Trigonometrický kruh ukazujúci os dotyčnicu a pythagorskú identitu tangens. (Vlastné rozpracovanie)

Pythagorská identita tangens

Pythagorská identita tangensu sa dá preukázať, ak sa zvažuje trojuholník obdĺžnika v B (obrázok 3) (obrázok 3). Aplikácia vety Pythagoras na uvedený trojuholník, ktorý musíte BQ² + Obrys² = OQ². Už sa však povedalo, že BQ = Tan (α), že OB = 1 a že OQ = sec (α), takže nahradenie rovnosti Pythagoras za pravý trojuholník OBQ, ktoré má:

Tak²(a) + 1 = sec²(α).

Príklad

Skontrolujte, či sú alebo nie sú pythagorské identity splnené v obdĺžnikovom trojuholníku katetos AB = 4 a BC = 3.

Riešenie: Kategórie sú známe, je potrebné určiť hypotenus, ktorá je:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Uhol ∡BAC sa bude nazývať a, ∡bac = α. Teraz sú určené trigonometrické dôvody:

Sin a = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = BC / AB = 3/4 

COTAN α = AB / BC = 4/3 

Sec a = ac / ab = 5/4 

CSC a = ac / bc = 5/3

Začína sa základnou trigonometrickou identitou:

SEN²(a) + cos²(a) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Dospelo sa k záveru, že je splnený.

- Ďalšou Pythagorovskou identitou je identita Tangent:

Tak²(a) + 1 = sec²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

A dospelo sa k záveru, že je overená identita tangens.

- Podobne to Cotangent:

Môže vám slúžiť: náhodné výbery s výmenou alebo bez výmeny

1 + ctg²(a) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Dospelo sa k záveru, že je tiež splnená, čo dokončilo úlohu overovať Pythagorovské identity pre daný trojuholník.

Vyriešené cvičenia

Otestujte nasledujúce identity na základe definícií trigonometrických dôvodov a pytagorických identít.

Cvičenie 1

Dokážte, čo cos² x = (1 + sen x) (1 - sin x).

Riešenie: Správny člen rozpoznáva pozoruhodný produkt násobenia binomialu jeho konjugátom, ktorý, ako je známe, je rozdiel štvorcov:

Cos² x = 1² - SEN² X

Potom termín s prsiami na pravej strane prechádza na ľavú stranu so zmeneným znakom:

Cos² X + sen² x = 1

Poznamenáva, že sa dosiahla základná trigonometrická identita, takže sa dospelo k záveru, že daný výraz je identita, to znamená, že je splnená pre akúkoľvek hodnotu x.

Cvičenie 2

Počnúc základnou trigonometrickou identitou a použitím definícií trigonometrických dôvodov na preukázanie pythagorskej identity harža.

Riešenie: Základná identita je:

SEN²(x) + cos²(x) = 1

Obaja členovia sú rozdelení medzi sen²(X) a menovateľ je distribuovaný v prvom členovi:

SEN²(x)/hriech²(x) + cos²(x)/hriech²(x) = 1/sen²(X)

Je to zjednodušený:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cottan (x) je identita (non -pythagorean), ktorá sa overuje definíciou trigonometrických dôvodov. Rovnakým spôsobom sa vyskytuje s nasledujúcou identitou: 1/sin (x) = csc (x).

Nakoniec musíte:

1 + ctg²(x) = CSC²(X)

Odkazy

1. Baldor J. (1973). Plochá geometria a priestor s úvodom do trigonometrie. Stredoamerický kultúrny. C.Do.
2. C. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Redakčná skupina Patria.
4. Iger. (s.F.). Matematika Tacaná. Iger.
5. Jr. Geometria. (2014). Polygóny. Lulu Press, Inc.
6. Miller, Heeren a Hornsby. (2006). Matematika: uvažovanie a aplikácie (desiate vydanie). Pearson Vzdelanie.
7. Patiño, m. (2006). Matematika 5. Redakčný progreso.
8. Wikipedia. Identity a vzorce trigonometrie. Obnovené z: je.Wikipedia.com