ICosagono

Čo je to Icogon?

A ICosagono alebo Isodecagon Je to polygón, ktorý má 20 strán. Polygón je plochá postava tvorená konečnou sekvenciou linkových segmentov (viac ako dva), ktoré uzavreli oblasť roviny.

Každý segment čiary sa nazýva bočná strana a priesečník každej páry strany sa nazýva vrchol. Podľa počtu strán dostávajú polygóny konkrétne názvy.

Najbežnejšie sú trojuholník, štvoruholník, Pentagon a šesťuholník, ktoré majú 3, 4, 5 a 6 strán, ale môžu byť postavené s požadovaným počtom strán strany.

Charakteristiky icogonu

Nižšie sú uvedené niektoré charakteristiky polygónov a ich aplikácia v icogone.

1- klasifikácia

Icosgono, ktorý je polygónom, možno klasifikovať ako pravidelné a nepravidelné, kde bežné slovo sa týka skutočnosti, že všetky strany majú rovnakú dĺžku a vnútorné uhly merajú rovnako; Inak sa hovorí, že iCosagon (polygón) je nepravidelný.

2- izodecagon

Pravidelný iCosgon sa tiež nazýva pravidelný izodogón, pretože na získanie pravidelného icosgon -geuge, čo by sa malo urobiť.

Obvod

Na výpočet obvodu „P“ pravidelného polygónu sa počet strán vynásobí dĺžkou každej strany.

V konkrétnom prípade icogonu sa obvod rovná 20xl, kde „L“ je dĺžka každej strany.

Napríklad, ak máte pravidelnú 3 cm bočnú iCosagon, jeho obvod sa rovná 20x3cm = 60 cm.

Je zrejmé, že ak je izokagon nepravidelný, predchádzajúci vzorec sa nedá použiť.

V takom prípade sa musí 20 strán pridať osobitne, aby sa získal obvod, to znamená, že obvod „p“ sa rovná ∑li, s i = 1,2,…, 20.

4- diagonálny

Počet diagonálov „D“, ktoré majú polygón, sa rovná n (n-3)/2, kde n predstavuje počet strán strany.

V prípade icogonu musí byť d = 20x (17)/2 = 170 diagonálov.

5- sumu vnútorných uhlov

Existuje vzorec, ktorý pomáha vypočítať súčet vnútorných uhlov pravidelného polygónu, ktorý je možné aplikovať na bežný iCosgon.

Vzorec spočíva v odpočítaní 2 na počet strán mnohouholníka a potom vynásobenie tohto čísla o 180 °.

Spôsob, akým sa tento vzorec získava, je to, že môžeme rozdeliť polygón N Strany do trojuholníkov N-2 a pomocou skutočnosti, že súčet vnútorných uhlov trojuholníka je 180 °, vzorec sa získava.

Na nasledujúcom obrázku je ilustrovaný vzorec pre pravidelný engon (9 -vedený polygón).

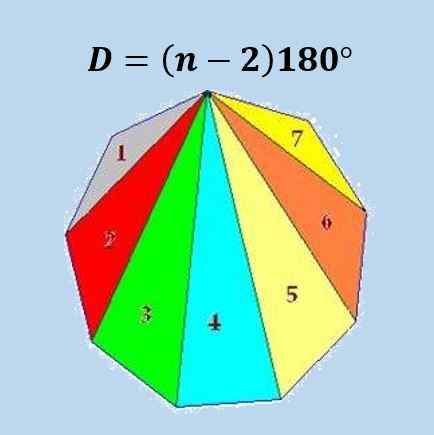
Pomocou predného vzorca sa získa, že súčet vnútorných uhlov akéhokoľvek iCosagonu je 18 × 180 ° = 3240 ° alebo 18π.

6

Na výpočet plochy pravidelného mnohouholníka je veľmi užitočné poznať koncept apothéme. Apotheme je kolmá čiara, ktorá prechádza zo stredu pravidelného polygónu do stredu ktorejkoľvek z jeho strán.

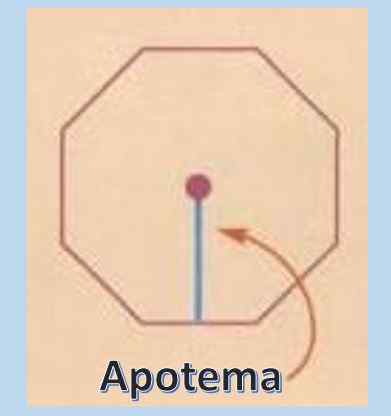
Akonáhle je známa dĺžka apotheme, plocha pravidelného polygónu je a = pxa/2, kde „p“ predstavuje obvod a „a“ apotheme.

V prípade pravidelného iCosagonu, ktorý máte do svojej oblasti, je a = 20xlxa/2 = 10xlxa, kde „L“ je dĺžka každej strany a „A“ jej apothéme.

Na druhej strane, ak máte nepravidelný polygón N strany, na výpočet jeho plochy je polygón rozdelený na známe trojuholníky N-2, potom sa vypočíta plocha každého z týchto trojuholníkov a nakoniec všetky tieto sú pridané oblasti.

Vyššie opísaná metóda je známa ako triangulácia polygónu.

Odkazy

1. Elementy geometrie: s mnohými cvičeniami a geometriou kompasu. University of Medellin.
2. Iger. (s.F.). Matematika Tacaná. Iger.