Matematika

Negatívna homotecia

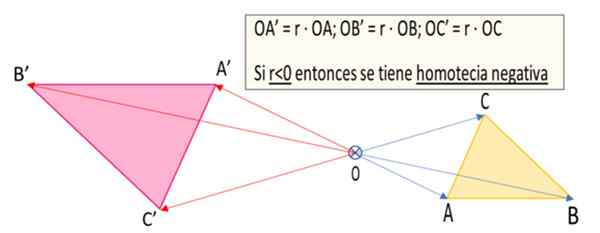
postava 1. Triangle a'b'c 'je homotická transformácia trojuholníka ABC vzhľadom na bod alebo z dôvodu negatívnej homotecie r = -1.5 (pripravené: f zapata).

Čo je negatívna homotecia?

Negatívna homotecia je transformácia, pri ktorej má polygón obsiahnutý v rovine ako svoj obraz iného polygónu v tej istej rovine, rovnakých uhlov a so zodpovedajúcimi stranami úmerný tým pôvodným. Keď je homotecia negatívna, obraz sa otáča polovicou otočenia vzhľadom na počiatočný obrázok.

Homotecia sa vyznačuje tým, že má centrum homotiecie Ani a proporcionalita konštanty nazývaná rozum r. Kedy r Je to záporné číslo, takže sa hovorí o negatívnej homotecia.

Ako sa robí transformácia homotiecie?

Aby sme vysvetlili, ako sa vykonáva negatívna homotekska ABC Kto chce vybudovať svoj negatívny homotikum.

1.- Začína si vyberať centrum homotiecie, čo je tento prípad Ani.

2.- Od Ani Orientované segmenty sú postavené (vektory) Oa, Obrys a Oc ktoré idú zo stredu Homotecia na každý z vrcholov trojuholníka.

3.- Vyberá sa homotecia r. Pretože chcete negatívnu homoteciu, potom r Musí to byť menej ako nula. V prípade obrázku 1 bolo vzaté R = -1.5.

4.- Vektory sú nakreslené Oa ', Obj ' a Oc ', ktoré sú Oa '= r ∙ oa, Ob '= r ∙ ob a OC '= R ∙ OC. Ako R = -1.5, To je záporné číslo, potom vektory Oa ', Obj ' a Oc ' Majú smer v rozpore s ich zodpovedajúcimi náprotivkami, to znamená Oa, Obrys a Oc. Ale ako absolútna hodnota rozumu r je | R | = 1.5 veľkosti Oa ', Obrys„A Oc ' Sú raz a pol väčšie ako v prípade ich náprotivkov Oa, Obrys a Oc.

5.- Tipy vektorov Oa ', Obj ' a Oc ' Definujte vrcholy trojuholníka A'b'c ' Aký je negatívny homotikum trojuholníka ABC.

Vlastnosti negatívnej homotecie

Ten negatívna homotecia, tiež nazývaný Inverzná homotecia, Má nasledujúce vlastnosti:

Môže vám slúžiť: násobky 8: Čo je a vysvetlenie

1.- Zodpovedajúce strany medzi obrazovým polygónom a pôvodným polygónom majú proporcionálne dĺžky, pričom konštanta proporcionality je absolútnou hodnotou pomeru homotiecie, to znamená, že obraz je zosilnený faktorom | r | tak dlho | r | je väčší ako jednotka, ale obraz sa zníži, ak | r | je menej ako jednotka.

2.- Uhly medzi zodpovedajúcimi stranami obrázka a pôvodným číslom majú rovnaké opatrenia.

3.- Homológne strany medzi originálnym a obrazom sú navzájom rovnobežné.

4.- Zodpovedajúce segmenty v prípade negatívnej homotecie sú paralelné, ale s vedením alebo opačným smerom. Napríklad na obrázku 1, segment AB má svoj homológny A'b 'paralelne s prvým, ale s opačným smerom.

Porovnanie s pozitívnou homoteciami

Nazýva sa pozitívna homotekska, v ktorej je pomer homotiecie pozitívnym počtom. Na vybudovanie pozitívnej homotecie sa sledujú rovnaké kroky ako negatívne homotécie:

1.- Vyberte si centrum Homotecia, v našom prípade Ani (Pozri obrázok 2).

2.- Nakreslite orientované segmenty (vektory), od stredu Homotecia po vrcholy polygónu, v prípade obrázku 2 sú: Oa, Obrys a Oc.

3.- Vyberte pomer homotiecie, ktorý je kladným číslom, napríklad v prípade, že bol vybraný R = 0.5.

4.- Vektory sú nakreslené Oa ', Obj ' a Oc ', ktoré sú Oa '= r ∙ oa, Ob '= r ∙ ob a OC '= R ∙ OC. Ako r Je to pozitívne číslo, potom vektory Oa ', Obj ' a Oc ' Majú rovnakú adresu ako Oa, Obrys a Oc. Dĺžky Oa ', Obrys„A Oc ' Sú polovica, že ich náprotivky Oa, Obrys a Oc, Pretože dôvod je R = 0.5.

5.- Nakoniec sú vrcholy A'B'C spojené, aby sa získal homotický trojuholník do ABC s dôvodom 1/2.

Môže vám slúžiť: štvornásobné: prvky, vlastnosti, klasifikácia, príklady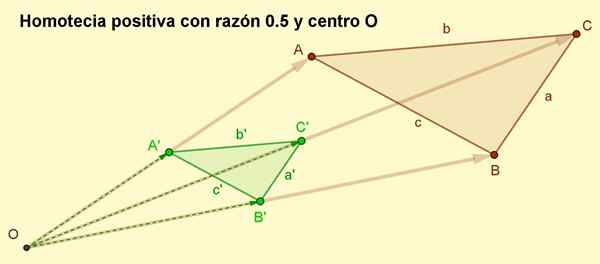

Obrázok 2. Pozitívne homotecia správne 0,5 výsledkov trojuholníka ABC. V pozitívnej homotecia sa zachováva orientácia. (Pripravený: f. Zapata)

Príklady homotiecie

Homotecia sa objavuje v rôznych situáciách:

Filmové projektory

Vo filmovom projektore sa premieta obrázok zaznamenaný v rámci a rozširuje sa na obrazovke a aby sa projekcia videla napravo, je potrebné, aby rámec investoval, pretože centrum homotiecie je v strede šošovky šošovka šošovky projektora, medzi rámom a obrazovkou (negatívna homotecia, pozri obrázok 3)

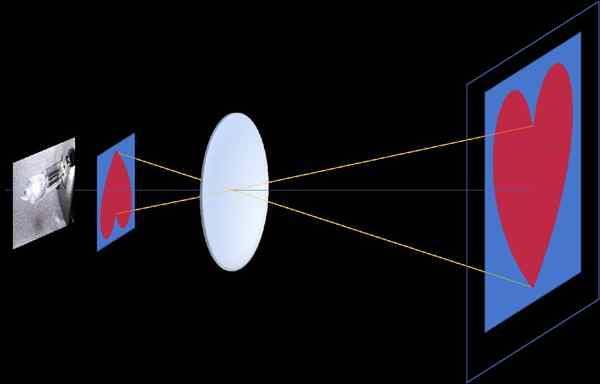Obrázok 3. Negatívna homotecia sa objaví vo filmovom projektore, medzi obrazom zaznamenaným na priesvitnom rámci a obrázkom premietaným na obrazovke. Centrum Homotecia sa nachádza v optickom stredisku objektívu, zase umiestnené medzi rámom a obrazovkou. Zdroj: f. Zapata.

Fotoaparáty

Tento princíp sa vzťahuje aj na fotoaparáty: Svetlo z obrázka umiestneného v určitej vzdialenosti od objektívu sa premieta na fotografickom senzore, ktorý môže byť ľahkým chemickým filmom alebo senzorom CCD, ak ide o digitálny fotoaparát.

Obrázok zaznamenaný v senzore je obrátený vzhľadom na skutočný a zvyčajne je úmerne menší ako ona.

Praktické uplatnenie

Slnko by nemalo vyzerať priamo, pretože spôsobuje trvalé poškodenie sietnice, ale existujú dve možnosti, ako ju študovať: používajte filtre, ktoré zoslabujú intenzitu svetla alebo premietajú jeho obraz na obrazovke.

Môže vám slúžiť: Proporcionálna variácia

Projekčné zariadenie pozostáva z dĺžkovej trubice d. Jeden z koncov trubice je pokrytý hliníkovou fóliou a vŕtačky v strede s kolíkom. Druhý koniec, ktorý bude slúžiť ako obrazovka, je pokrytý priesvitným papierom, ktorý môže byť cibuľový papier alebo papier z albanénu (rastlinný papier).

Cvičenie

Určite priemer slnka, s vedomím, že suchozemský orbitálny polomer je rádovo 150 miliónov kilometrov, že projekčná trubica, ako je trubica znázornená na obrázku 4, má dĺžku 2,2 metrov a že projektovaný obraz je 2, 1 cm s priemerom.

Obrázok 4. V trubici na premietnutie solárneho disku sa vyskytuje negatívny pomer homotiecie. Zdroj: f. Zapata.

Riešenie

Údaje sú nasledujúce:

Dĺžka trubice: D = 2,2 m
Premietaný obrazový priemer obrazu Sun: S = 2,1 cm
Vzdialenosť od slnečnej trubice: R = 150 x 10^9 m
Skutočný priemer slnka: S = ¿?

Na získanie priemeru slnka sa pomer proporcionality používa podľa proporcionality homotecie (pozri obrázok 4):

Vzdialenosť od slnka je na dĺžke trubice, pretože priemer slnka je na priemer premietaného obrázka:

(R / d) = (s / s)

Vyčistenie tejto rovnosti, že skutočný priemer slnka má priemer projekcie vynásobený kvocientom medzi vzdialenosťou k slnku a dĺžkou trubice:

S = s (r / d)

Umiestnenie numerických hodnôt sú:

S = 2,1 x 10^-2 M (150 x 10⁹ m / 2,2 m)

S = 1,43 x 10⁹ m.

Tento výsledok sa interpretuje takto: Skutočný priemer slnka je 1,43 milióna kilometrov.

Odkazy

Álvaro Rendón, do. R. 2004. Technická kresba: Notebook aktivity.
Antonio Álvarez de la Rosa, J. L. 2002. Afinita, homológia a homotecia.
Baer, r. 2012. Lineárna algebra a projektívna geometria. Couer Corporation.
Hebert a. 1980. Všeobecná matematika, pravdepodobnosti a štatistika.
Messerve, b. A. 2014. Základné koncepty geometrie. Couer Corporation