Matematika

Hyperbola

4437
1235
Alfréd Blaho

Čo je hyperbola?

Hyperbola je súbor bodov roviny tak, že absolútna hodnota rozdielu medzi vzdialenosťami na dva pevné body, nazývané bodové svetlá, zostáva konštantná. Táto sada bodov tvorí krivku s dvoma vetvami pozorovanými na obrázku 1.

Je tu bod p (x, y), ohnisko f₁ a f₂ oddelila vzdialenosť rovnajúcu sa 2C. Matematický spôsob vyjadrenia tohto vzťahu prechádza:

$\left |d__P_1-d__P_2 \right |=constante$

postava 1. Hyperbola s horizontálnou ohniskovou osou. Zdroj: f. Zapata.

Všetky body hyperboly spĺňajú túto podmienku, ktorá vedie k rovnici hyperboly, ako bude vidieť neskôr. Stred medzi reflektormi sa nazýva stred C a na obrázku sa zhoduje s bodom (0,0), ale hyperbola sa môže tiež posunúť a jeho stred zodpovedá inému súradnicovému bodu C (H, K).

Na hornej postave je os x ohniskovou osou hyperboly, pretože existujú reflektory, ale môžete tiež postaviť ten, ktorého ohniskovou osou je os a os a os a.

Hyperbola je súčasťou kriviek známych ako kužeľový, Hovorí sa im to preto, že ich možno odvodiť od strihu kužeľa s plochou sekciou. Hyperbola sa získa pri pretínaní kužeľa a roviny za predpokladu, že neprechádza vrcholom kužeľa a uhol, ktorý tvorí rovinu s osou kužeľa istota.

Spolu s podobenstvom, obvodom a elipou sú kužeľ známy už od staroveku. Grécky matematik Apollonius z Perga (262-190 pred Kristom) napísal zmluvu o geometrii, v ktorej podrobne opísal svoje vlastnosti a sám im dal mená, s ktorými sa navzájom poznajú dodnes.

Charakteristiky hyperboly

Toto sú niektoré z najvýznamnejších charakteristík hyperboly:

Je to plochá krivka, preto stačí dať súradniciam (x, y) každého bodu, ktorý k nemu patrí.
Je to tiež otvorená krivka, na rozdiel od obvodu alebo elipsy.
Má dve vetvy usporiadané symetricky.
Vertikálna os, ako aj horizontálna os sa môžu považovať za osi symetrie, ale os, kde sa bodové svetlá nazývajú ohnisková os alebo hlavná os.
Je to symetrické vzhľadom na jeho centrum.
Hyperbola pretína ohniskovú os v dvoch bodoch nazývaných Vrcholy, Preto sa ohnisková os niekedy volá skutočná os, zatiaľ čo sa volá druhá os Imaginárna os, Pretože nemá žiadne body spoločné s hyperbolou.
Stred hyperboly sa nachádza na polceste medzi bodmi nazývanými ložiskami.
Je spojený s dvoma veľmi konkrétnymi čiarami nazývanými asymptoty, ktoré sú čiarymi, ku ktorým sa hyperbola blíži, ale bez ich prekročenia, keď sú hodnoty x e y veľmi veľké. Asymptoty sa pretína v strede hyperboly.

Môže vám slúžiť: Prepríjemná funkcia: Definícia, vlastnosti, príklady

Rovnice a vzorce

Hiperbolova rovnica so stredom v (0,0)

Počnúc od definície uvedenej na začiatku:

$\left |d__P_1-d__P_2 \right |=constante$

Na túto pozitívnu konštantu sa zvyčajne nazýva 2a a je to vzdialenosť, ktorá oddeľuje vrcholy hyperboly, potom:

$\left |d__P_1-d__P_2 \right |=2a$

Na druhej strane, DP₁, Dp₂ a 2c sú strany trojuholníka znázornené na obrázku 1 a podľa elementárnej geometrie je odčítanie štvorcov strany akéhokoľvek trojuholníka vždy menšie ako štvorec zostávajúcej strany. Tak:

4²< 4c²

do < c

Tento výsledok bude čoskoro užitočný.

Ako vzdialenosť medzi dvoma bodmi P₁(X₁,a₁) A p₂(X₂,a₂) je:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

Nahradením súradníc P (x, y), f₁(-C, 0) a f₂(C, 0) Zostáva:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Čo je rovnocenné:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Štvorcový v oboch členoch, aby ste odstránili korene a reorganizovali podmienky, ktoré dosiahnete:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

Do množstva C² - do², čo je vždy kladné množstvo, pretože < c, se la denomina b², Preto je uvedené vyššie ako:

b²X² - do²a² = a² b²

Rozdelenie všetkých výrazov podľa² b², Je to hyperbola rovnica zameraná na (0,0) s horizontálnou reálnou osou:

$\fracx^2a^^2-\fracy^2b^^2=1$

S A a B väčším ako 0. Táto rovnica sa volá Kanonická rovnica Hyerbola a menovateľ² Vždy to zodpovedá pozitívnej frakcii.

Hyperbola sústredená na (0,0) a so vertikálnou osou skutočnou osou má formu:

$\fracy^^2a^2-\fracx^^2b^2=1$ Križovatky hyperboly s súradnicovými osami

Križovatky hyperboly so súradnicovými osami sa vykonávajú y = 0 a x = 0 v rovnici:

Pre y = 0

X² /² = 1 ⇒ x² = a²

x = ± a

Hyperbola sa zníži na os x v dvoch bodoch nazývaných vrcholy, ktorých príslušné súradnice x sú: x = a y x = -a

Pre x = 0

Získa sa -a² /b² = 1, ktorý nemá skutočné riešenie a vyplýva, že hyperbola sa nereá na vertikálnu os.

Hyperbola rovnica so stredom v (H, k)

Ak je stred hyperboly v bode C (H, k), potom jej kanonická rovnica je:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Hiperbola

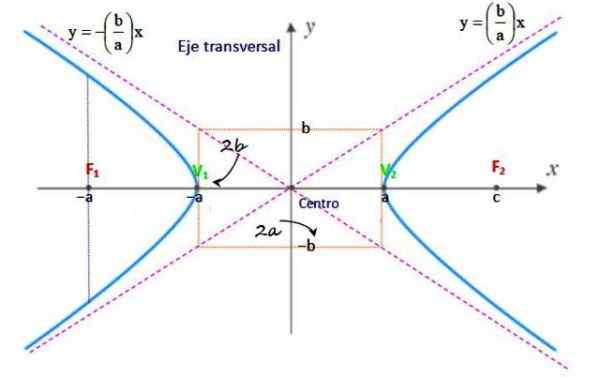Obrázok 2. Hiperbola. Zdroj: f. Zapata.

Stred

Je to stred segmentu f₁F₂A jeho súradnice sú (h, k) alebo (x_ani,a_ani).

Môže vám slúžiť: Syntetické rozdelenie

Foky

Sú to dva pevné body f₁ a f₂ ktoré sú na skutočnej osi hyperboly, s ohľadom na ktorým zostáva rozdiel vzdialeností do bodu p (x, y) konštantný. Vzdialenosť medzi reflektormi a stredom hyperboly je „C“.

Vektorové rádio

Toto sa nazýva vzdialenosť medzi bodom P a jedným z bodových reflektorov.

Ohnisková vzdialenosť

Je to vzdialenosť, ktorá oddeľuje oba reflektory a zodpovedá 2C.

Vrcholy

Vrcholy v₁ a v₂ Sú to body, kde hyperbola pretína skutočnú os. Vrchol a stred hyperboly sú oddelené vzdialenosťou A, a preto vzdialenosť medzi vrcholmi je 2A.

Ohnisková os, hlavná os alebo skutočná os

Je to os, kde sú bodové reflektory umiestnené a meria 2c. Môže byť umiestnený na ktorejkoľvek z dvoch karteziánskych osí a hyperbola ju pretína v bodoch nazývaných vrcholy.

Priepustná os, sekundárna os alebo imaginárna os

Je to os kolmá na ohniskovú os a meria 2b. Hyperbola ju nepretína, takže sa tiež nazýva imaginárna os.

Asymptoty

Sú to dve riadky, ktorých príslušné čakajúce sú m₁ = (b/a) a m₂ = - (b/a), ktoré sú určené v strede hyperboly. Krivka nikdy pretína tieto čiary a produkt medzi vzdialenosťami akéhokoľvek bodu hyperboly na asymptoty, je konštantná.

Ak chcete nájsť rovnice asymptotov, stačí zladiť ľavú stranu kanonickej rovnice Hyperbola s 0. Napríklad pre hyperbolu zameranú na pôvod:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Obdĺžnik

Je to obdĺžnik, ktorého šírka je vzdialenosť medzi vrcholmi 2a a vzdialenosťou 2b a je zameraná na stred hyperboly. Jeho konštrukcia uľahčuje manuálne usporiadanie hyperboly.

Priama strana

Lano, ktoré prechádza jedným z bodových reflektorov, kolmo na skutočnú os.

Excentricita

Je definovaný ako kvocient medzi ohniskovou vzdialenosťou a skutočnou osou:

E = c/a

Je vždy väčší ako 1, pretože C je väčší ako A a menej ako √2.

Hodnota a naznačuje, či je hyperbola pomerne uzavretá (úzky obdĺžnik, predĺžený v smere hlavnej osi) alebo otvorený (široký obdĺžnik, predĺžený v smere imaginárnej osi).

Rovná dotyčná do hyperboly v bode P (x₁,a₁)

Dotyčnica k hyperbole v bode P (x₁,a₁) Je to bisektor dvoch rádiových vektorov tohto bodu.

Pre hyperbolu s hlavnou osou rovnobežnou s osou x je sklon čiary dotýkal hyperboly v bode P (x₁,a₁) je daný:

Môže vám slúžiť: kombinované operácie

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

A ak je hyperbola hlavnou osou rovnobežnou s osou y, potom:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Príklady hyperboly

Disperzia alfa častíc jadrom

Bombardovaním atómových jadier alfa časticami, ktoré nie sú ničím iným ako jadrami hélia. Tieto jadrá hélia sú dispergované po hyperbolických trajektóriách.

Trajektórie orgánov slnečnej sústavy

Obrázok 3: Planéty solárnych systémov

V slnečnej sústave sa objekty pohybujú pod pôsobením gravitačnej sily. Opis pohybu je odvodený z diferenciálnej rovnice, v ktorej je sila konzervatívna a nepriamo úmerná štvorcovej vzdialenosti. A riešenia tejto rovnice sú možné trajektórie, ktoré sledujú objekty.

Tieto trajektórie sú vždy kónické: obvody, elipsy, podobenstvá alebo hyperboly. Prvé dva sú zatvorené krivky, a takto sa pohybujú planéty, ale niektoré kométy sú stále otvorené trajektórie, ako sú podobenstvá alebo hyperboly, so slnkom sa nachádza v jednom z bodových reflektorov.

Minimálny zvuk

Ak existujú dva zdroje zvuku, ako napríklad dva reproduktory, ktoré emitujú zvuky rovnomerne vo všetkých smeroch, umiestnené pozdĺž priamky, minimá intenzity zvuku (deštruktívne rušenie) sú na hyperbole, ktorej hlavná os je uvedená čiara a v bodových reflektoroch Hyperbola sú reproduktory.

Cvičenie

Nájdite prvky nasledujúcej hyperboly: vrcholy, ložiská a asymptoty hyperboly a zostavte jej graf:

$\fracx^^216-\fracy^^24=1$

Riešenie

Stred tejto hyperboly sa zhoduje s pôvodom súradníc a jeho skutočná os je horizontálna, pretože kladná frakcia zodpovedá premennej x.

Hyperbola semixy sú:

do² = 16 ⇒ a = 4

b² = 4 ⇒ b = 2

Týmto spôsobom centrálny obdĺžnik meria 4 jednotky široké a 2 jednotky vysoké. Pamätajte na to, že to bolo uvedené vyššie² - do²= b², tak:

c² = a²+ b² ⇒ c² = 16 + 4 = 20

Preto je ohniskovým semifotografom:

C = √20 = 2√5

A ložiská sú v súradniciach₁ (-2√5.0) a f₂ (2√5.0).

Svahy asymptotov sú:

m = ± (b/a) = ± (2/4) = ± 0.5

Preto sú príslušné rovnice každého z nich:

a₁ = 0.5x; a₂ = -0.5x

Hyperbola sa môže ľahko grafovať prostredníctvom online softvéru ako Geogebra:

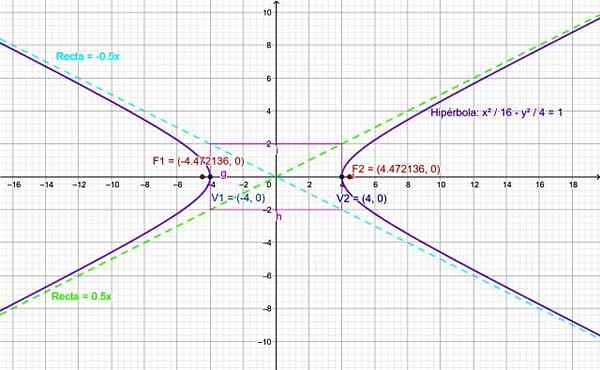Obrázok 4. Graf pre hyperbolu cvičenia vyriešené. Zdroj: f. Zapata.

Odkazy

Fisicalab. Rovnica hyperboly. Získané z: Fisicalab.com
Hoffman, J. Výber matematických problémov. Zväzok 2.
Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
Vesmír. Hyperbola. Získané z: Universoformulas.com
Zill, D. 1984. Algebra a trigonometria. McGraw Hill.

Hyperbola

Čo je hyperbola?

Charakteristiky hyperboly