Definícia hypercubo, rozmery, súradnice, rozvinuté

A hypercubo je kocka rozmeru n. Konkrétny prípad dimenzie Hypercubo sa nazýva Tesnenie. Hypercubo alebo N-Cubo sa skladá z priamych segmentov, všetky rovnaké dĺžky, ktoré sú vo svojich vrcholoch ortogonálne.

Ľudské bytosti vnímajú trojrozmerný priestor: široký, vysoký a hĺbkový, ale nie je možné, aby sme vizualizovali hypercubo dimenzie väčšie ako 3. 

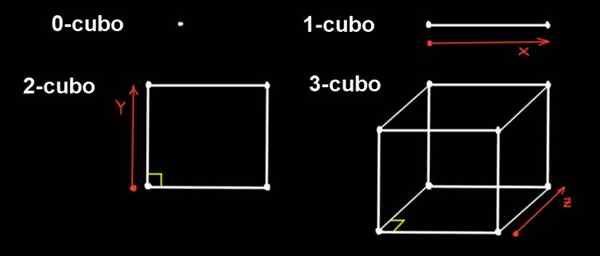
postava 1. 0-CUBO je bod, ak tento bod rozširuje v jednom smere vzdialenosť 1-CUBO, ak tento 1-CUBO rozširuje vzdialenosť v ortogonálnom smere, je 2-CUBO (od strán do x a), Ak 2-CUBO rozšíri vzdialenosť v ortogonálnom smere, je tu 3-cubo. Zdroj: f. Zapata.

Môžeme robiť projekcie v trojrozmernom priestore, aby sme ho reprezentovali, podobne ako premietame kocku v lietadle, aby ju reprezentovala.

V rozmere 0 je jediný obrázok, takže 0-CUBO je bod. 1-CUBO je priamy segment, ktorý sa tvorí presunutím bodu v vzdialenosti k vzdialenosti k.

Zo svojej časti 2-CUBO je štvorec. Je postavený presídlením 1-CUBO (segment dlhý a) v smere a ktorý je ortogonálny k adrese X, vzdialenosť od.

3-CUBO je bežná kocka. Je postavený od štvorca, ktorý vytlačí to isté v treťom smere (z), ktorý je ortogonálny do smerov x a y, vzdialenosť do.

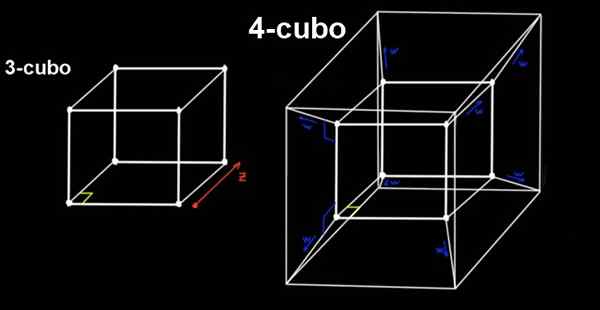Obrázok 2. 4-CUBO (Testeract) je rozšírenie 3-CUBO v ortogonálnom smere k trom konvenčným priestorovým adresám. Zdroj: f. Zapata.

4-CUBO je pokus, ktorý je postavený z 3-CUBO, ktorý posunie rovnaké ortogonálne, vzdialenosť do, smerom k štvrtej dimenzii (alebo štvrtému smeru), ktorý nemôžeme vnímať.

Spúšťač má všetky svoje priame uhly, má 16 vrcholov a všetky jej hrany (celkom 18) majú rovnakú dĺžku do.

Ak je dĺžka hrán n-cubo alebo hypercubo dimenzie n 1, potom je to jednotková hypercubo, v ktorej najdlhšie diagonálne opatrenia √n.

Môže vám slúžiť: lineárne programovanie: Na čo ide, modely, obmedzenia, aplikácieObrázok 3. N-cubo sa získa z (n-1) -cubo, ktorý ho predlžuje ortogonálne v ďalšej dimenzii. Zdroj: Wikimedia Commons.

[TOC]

Aké sú rozmery?

Rozmery sú stupne voľnosti alebo možné smery, v ktorých sa môže objekt pohybovať.

V rozmere 0 nie je možné pohnúť sa a jediným možným geometrickým objektom je bod.

Rozmer v euklidovskom priestore je reprezentovaný orientovanou čiarou alebo osou, ktorá definuje tento rozmer, nazývaná os x. Oddelenie dvoch bodov A a B je euklidovská vzdialenosť:

D = √ [(x_do - X_b)²]. 

V dvoch rozmeroch je priestor znázornený dvoma ortogonálnymi čiarami, ktoré sa navzájom nazývajú x a osi.

Poloha akéhokoľvek bodu v tomto dvojrozmernom priestore je daná dvojicou karteziánskych súradníc (x, y) a vzdialenosť medzi dvoma bodmi A a B

D = √ [(x_do - X_b)² + (a_do - a_b)²]

Pretože je to priestor, v ktorom je splnená euklid geometria.

Tri rozmerový priestor

Tri -dimenzionálny priestor je priestor, v ktorom sa pohybujeme. Má tri smery: šírka, vysoká a hĺbka.

V prázdnej miestnosti kolmé rohy navzájom dávajú tieto tri smery a každému z nich môžeme spojiť os: x, y, z.

Tento priestor je tiež euklidian a vzdialenosť medzi dvoma bodmi A a B sa vypočíta takto:

D = √ [(x_do - X_b)² + (a_do - a_b)² + (z_do - z_b)²]

Ľudské bytosti nemôžu vnímať viac ako tri priestorové rozmery (alebo Euclideas).

Z prísne matematického hľadiska je však možné.

V tomto priestore má bod súradnice: (x1, x2, x3, ..., xn) a vzdialenosť medzi dvoma bodmi je: 

D = √ [(x₁ - X_{1 b})² + (X_Druhý - X_2B)² +... + (x_nat - X_Nb)²].

Môže vám slúžiť: Hypergeometrické rozdelenie: vzorce, rovnice, model

Štvrtý rozmer a čas

V skutočnosti sa v teórii času relativity zaobchádza ako s ďalším rozmerom a súradnica je spojená.

Je však potrebné objasniť, že táto súradnica spojená s časom je imaginárne číslo. Preto oddelenie dvoch bodov alebo udalostí v priestore nie je Euclidiana, ale sleduje metriku Lorentza.

Štvorrozmerný hypercubo (spúšť) nežije v priestore, patrí do štvorrozmerného euklideálneho hyper-priestoru. 

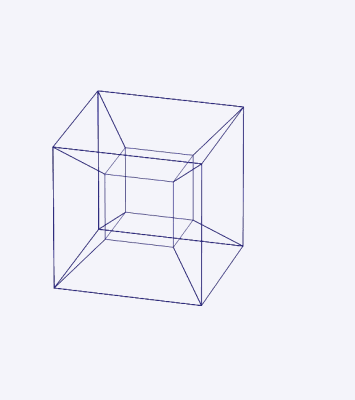
Obrázok 4. 3D projekcia štvorrozmerného hypercubo v jednoduchej rotácii okolo roviny, ktorá rozdeľuje prednú postavu doľava, späť doprava a zhora nadol. Zdroj: Wikimedia Commons.

Súradnice Hypercubo

Súradnice vrcholov N-CUBO zamerané na pôvod sa dosahujú tak, že všetky možné permutácie nasledujúceho výrazu:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Kde a je dĺžka okraja.

-On zväzok Z okraja okraja A je: (A/2)ⁿ (2ⁿ) = aⁿ.

-Ten najdlhší diagonálny Je to vzdialenosť medzi opačnými vrcholmi.

-Nasledujúce sú opačné vrcholy na štvorci: (-1, -1) a (+1, +1).

-A v a Kocka: (-1, -1, -1) a (+1, +1, +1). 

-Ten najdlhší diagonálny opatrení N-CUBO: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

V tomto prípade sa predpokladalo, že strana je a = 2. Pre stranu N-Cubo pre každého zostane:

d = a√n.

-Pokus má každý zo svojich 16 vrcholov pripojených k štyrom okrajom. Nasledujúci obrázok ukazuje, ako sú vrcholy spojené v spúšťači.

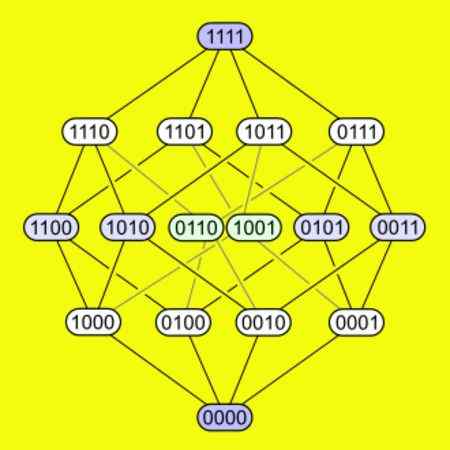Obrázok 5. Zobrazí sa 16 vrcholov štvorrozmerného hypercubo a ako sa spájajú rovnako. Zdroj: Wikimedia Commons.

Rozvinul hypercubo

Pravidelná geometrická postava, napríklad polyhedron, sa dá rozvinúť na niekoľkých číslach s nižšou dimenziou.

V prípade 2-CUBO (štvorec) sa dá rozvinúť v štyroch segmentoch, to znamená štyri 1-CUBO.

Môže vám slúžiť: Poisson Distribúcia: vzorce, rovnice, model, vlastnosti

Podobne sa dá rozložiť 3-CUBO v šiestich 2-CUBO.

Obrázok 6. N-CUBO sa dá rozvinúť v niekoľkých (n-1) -cubos. Zdroj: Wikimedia Commons.

4-CUBO (testerac) sa môže rozvinúť v ôsmich 3-CUBO.

Nasledujúca animácia ukazuje rozvíjanie drôtu.

Obrázok 7. 4 -rozmerový hypercubo sa môže rozvinúť na ôsmich troch rozmerových kocky. Zdroj: Wikimedia Commons. Obrázok 8. Tri -rozmerná projekcia štvorrozmerného hypercubo, ktorý robí dvojitú rotáciu okolo dvoch ortogonálnych rovín. Zdroj: Wikimedia Commons.

Odkazy

1. Vedecká kultúra. Hypercubo, vizualizácia štvrtej dimenzie. Zdroj: CulturacecientificA.com
2. Epsilón. Tetradimenzionálny hypercubo alebo tesseratt. Obnovené z: epsilones.com
3. Perez R, Aguilera A. Metóda na získanie pokusu zo vývoja Hypercubo (4D). Získané z: ResearchGate.slepo
4. Wikilibros. Matematika, polyhedra, hypercubes. Obnovené z: je.Wikibooks.orgán
5. Wikipedia.  Hypercube. Zdroj: In.Wikipedia.com
6. Wikipedia. Troska. Zdroj: In.Wikipedia.com