Matematika

Vlastnosti HeptadeCágono, diagonály, obvod, oblasť

Vlastnosti HeptadeCágono, diagonály, obvod, oblasť

On heptadecágono Je to pravidelný polygón 17 strán a 17 vrcholov. Jeho konštrukcia je možné vykonať v euklidovskom štýle, to znamená, že používa iba pravidlo a kompas. Bol to veľký génius matematiky Carl Friedrich Gauss (1777-1855), ktorý počítal iba 18 rokov, ktorý našiel postup pre jeho výstavbu v roku 1796. 

Zdá sa, že Gauss sa vždy cítil veľmi naklonený tejto geometrickej postave do tej miery, že odo dňa, keď objavil svoju výstavbu, sa rozhodol byť matematikmi. Hovorí sa tiež, že chce, aby bol HeptadeCágono zaznamenaný na jeho náhrobku.

postava 1. HeptadeCágono je pravidelný polygón 17 strán a 17 vrcholov. Zdroj: f. Zapata.

Gauss tiež zistil, že vzorec na určenie, ktoré pravidelné polygóny majú možnosť postaviť sa s pravidlom a kompasom, pretože niektorí nemajú presnú euklidovskú konštrukciu.

[TOC]

Charakteristiky HeptadeCágono

Pokiaľ ide o jeho charakteristiky, rovnako ako každý polygón, je dôležitý súčet jeho vnútorných uhlov. V pravidelnom mnohouholníku n strany, suma je daná:

SA (n) = (n -2) *180 °.

Pre HeptadeCágono počet strán n je 17, Čo znamená, že súčet jeho vnútorných uhlov je:

SA (17) = (17 - 2) * 180 ° = 15 * 180 ° = 2700 °.

Táto suma, vyjadrená v Radiane, je takáto:

Sa (17) = (17 - 2) * π = 15 * π = 15π

Z predchádzajúcich vzorcov sa dá ľahko odvodiť, že každý vnútorný uhol heptadecágono má presné α opatrenie dané:

a = 2700 °/17 = (15/17) π radiany

Z toho vyplýva, že vnútorný uhol približne je:

α ≈ 158 824 °

Diagonála a obvod

Diagonálne a obvody sú ďalšie dôležité aspekty. V akomkoľvek mnohouholníku je počet diagonálov: 

D = n (n - 3) / 2 a v prípade HeptadeCágona, napríklad N = 17, Musíš D = 119 diagonála.

Môže vám slúžiť: trinomial

Na druhej strane, ak je známa dĺžka každej strany HeptadeCágono, potom obvod pravidelného HeptadeCágonu jednoducho pridáva 17 -krát túto dĺžku alebo čo je rovnocenné 17 -násobkom dĺžky d Na každej strane:

P = 17 d

Obvod HeptadeCágono 

Niekedy je známe iba rádio r z HeptadeCágono, preto je potrebné pre tento prípad vyvinúť vzorec.

Za týmto účelom koncept apotém. Apotheme je segment, ktorý prechádza zo stredu pravidelného polygónu do stredu na jednej strane. Apotém v porovnaní so stranou je kolmá na túto stranu (pozri obrázok 2).

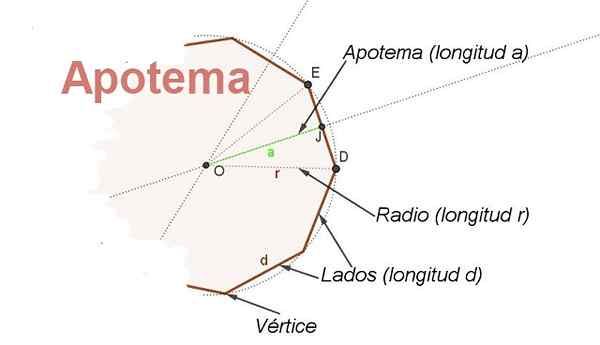Obrázok 2. Sú zobrazené časti pravidelného rádiového polygónu a jeho apothém. (Vlastné rozpracovanie)

Okrem toho je apothémia uhlom s stredným vrcholom a stranami na dvoch po sebe idúcich vrcholoch polygónu, čo umožňuje nájsť vzťah medzi rádiom r a strana d.

Ak sa volá p do centrálneho uhla Laň A berúc do úvahy tento apothém Oj je bisektor, ktorý máš Ex = d/2 = r sen (p/2), kde máte vzťah na nájdenie dĺžky d na strane polygónu známe jeho rádio r a jeho centrálny uhol p:

D = 2 r sin (p/2)

V prípade HeptadeCágonu β = 360 °/17 Za to, čo máte:

D = 2 r sen (180 °/17) ≈ 0,3675 r

Nakoniec je získaný vzorec obvodu HeptadeCágona známy jeho polomer:

P = 34 r sen (180 °/17) ≈ 6.2475 R

Obvod heptadecágonónu PCIR = 2π r ≈ 6.2832 r.

Oblasť

Aby sme určili oblasť HeptadeCágono, budeme sa odvolávať na obrázok 2, ktorý zobrazuje strany a apothémia pravidelného polygónu n strany. V tomto čísle trojuholník Eod Má oblasť rovnajúcu sa základne d (Polygon Strana) podľa výšky do (Polygon apothém) vydelený 2:

Môže vám slúžiť: Séria energie: príklady a cvičenia

EOD = (d x a) / 2

Takže to známe apothéme do heptadecágona a strany d to isté je:

HeptadeCágono Area = (17/2) (D X A)

Plocha vzhľadom na stranu

Ak chcete získať receptúru pre oblasť HeptadeCágono s vedomím dĺžky jej sedemnástich strán, je potrebné dosiahnuť vzťah medzi dĺžkou apotheme do a strana d.

V súvislosti s obrázkom 2 máte nasledujúci trigonometrický vzťah:

Tan (p/ 2) = napr/ oj = (d/ 2)/ a, bytosť p do centrálneho uhla Laň. Takže ten apothém do dá sa vypočítať, ak je známa dĺžka d zo strany mnohouholníka a stredného uhla p:

A = (d/2) COTAN (β/2)

Ak je tento výraz pre apothém nahradený teraz, vo vzorci oblasti HeptadeCágono získanej v predchádzajúcej časti máte:

HeptadeCágono Area = (17/4) (D2) Cotan (β/2)

Bytosť β = 360 °/17 Pre HeptadeCágono, takže konečne máte požadovaný vzorec:

HeptadeCágono Area = (17/4) (D2) Cotan (180 °/17)

Oblasť vzhľadom na rádio

V predchádzajúcich oddieloch bol nájdený vzťah medzi D. Strana pravidelného polygónu a jeho Rádiom R, nasledujúce: toto: toto: toto bytie:

D = 2 r sin (p/2)

Tento výraz pre d Sa zavádza do výrazu získaného v predchádzajúcej časti oblasti. Ak sa vykonajú príslušné substitúcie a zjednodušenie, získa sa vzorec, ktorý umožňuje vypočítať oblasť HeptadeCágono:

HeptadeCágono Area = (17/2) (r2) Sin (β) = (17/2) (r2) Sen (360 °/17)

Približný výraz pre túto oblasť je:

HeptadeCágono Area = 3 0706 (r2) 

Ako sa očakávalo, táto oblasť je o niečo menšia ako oblasť kruhu, ktorý ohraničuje HeptadeCágon DoObvod = π r2 ≈ 3 1416 r2. Presnejšie povedané, je o 2% nižšie ako kruh jeho ohraničeného kruhu.

Môže vám slúžiť: Oblasť pravidelného a nepravidelného Pentagónu: Ako sa užíva, cvičenia

Príklady

Príklad 1

Aby mal HeptadeCágono 2 cm strany, akú hodnotu by mal mať polomer a priemer ohraničeného obvodu? Nájdite tiež obvodovú hodnotu.

Na zodpovedanie otázky je potrebné pamätať na vzťah medzi bokom a polomerom pravidelného polygónu N strany:

 D = 2 r sen (180 ° / n)

Pre heptadecágono N = 17, preto D = 0,3675 r, Inými slovami

S priemerom 10 8844 cm.

Obvod 2 cm strany HeptadeCágon je p = 17* 2 cm = 34 cm.

Príklad 2

Koľko stojí oblasť pravidelnej strany HeptadeCágono de 2 cm?

Je potrebné odvolať sa na vzorec demonštrovaný v predchádzajúcej časti, ktorá umožňuje nájsť oblasť heptadecágona, keď je dĺžka d Na jeho strane:

HeptadeCágono Area = (17/4) (D2) / Opálenie (180 ° / 17) 

Pri výmene D = 2 cm v prednom vzorci sa získa:

Oblasť = 90,94 cm

Odkazy

  1. C. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
  2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Redakčná skupina Patria.
  3. Oslobodený, k. (2007). Objavovať polygóny. Benchmark vzdelávacia spoločnosť.
  4. Hendrik, v. (2013). Zovšeobecnené polygóny. Birkhäuser.
  5. Iger. (s.F.). Matematika Tacaná. Iger.
  6. Jr. Geometria. (2014). Polygóny. Lulu Press, Inc.
  7. Miller, Heeren a Hornsby. (2006). Matematika: uvažovanie a aplikácie (desiate vydanie). Pearson Vzdelanie.
  8. Patiño, m. (2006). Matematika 5. Redakčný progreso.
  9. Sada, m. Pravidelných 17 strán s pravidlom a kompasom. Získané z: Geogebra.orgán
  10. Wikipedia. Heptadecágono. Obnovené z: je.Wikipedia.com